- The Tower of Hanoi is one of the main recursion applications. It says, “If you can solve n-1 cases then you can easily solve the nth case”.
- The main problem in Hanoi towers is moving all the rings from the source tower to the destination tower. The tower is also called a peg or hole.
- The tower’s rings are arranged so that the topmost ring or first ring will be smaller than the second ring, the second ring, the third ring, and so on.
- When we transfer the rings from the source tower to the destination tower we have to maintain the rings.
- At a time we can move only one ring. While transferring the rings from the source tower to the destination tower we can use another tower called an intermediate tower or auxiliary tower which is present between the source and destination towers.
- To summarize the solution for the towers of Hanoi problem the base case is if n=1, move the ring from source to destination using auxiliary.
Recursive case n>1
- Move n-1 rings from source to auxiliary with the help of destination.
- Move the ring from source to destination using the auxiliary.
- Move n-1 rings from auxiliary to destination using source.
The number of rings to move n rings in this problem is given by 2n-1.
Ex:
n=1, Moves are 1.
n=2, Moves are 3.
n=3, moves are 7.
n=4, moves are 15.
Tower of Hanoi Algorithm
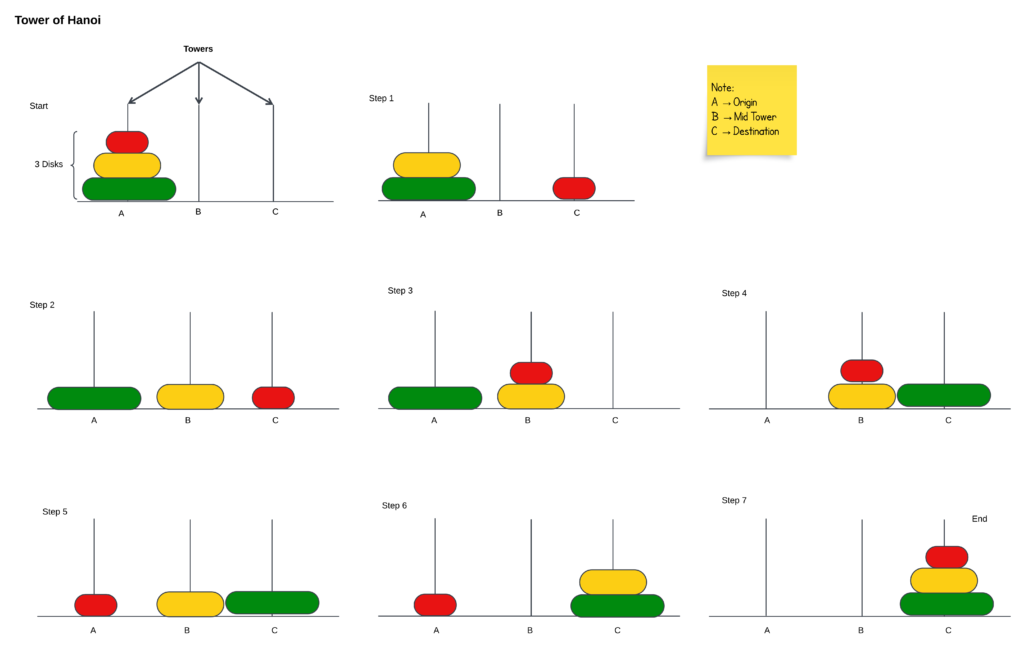
- Identify:
- Source Tower(A): Where all the disks start stacked, the smallest on top.
- Auxiliary Tower(B): Used as a temporary holding area.
- Destination Tower(C): Where you want to move the entire stack.
- Move Tower (Recursive Function):
- Base Case: If there’s only one disk, move it directly from the source tower to the destination tower.
- Recursive Case:
- Move the top n-1 disks from the source tower to the auxiliary tower (using the destination tower as a temporary holder).
- Move the largest disk (the bottom one) from the source tower to the destination tower.
- Move the n-1 disks from the auxiliary tower to the destination tower (using the source tower as a temporary holder).
Steps of Tower of Hanoi Algorithm
Start: All three disks are stacked on tower A.
- Step 1: The smallest disk is moved from A to C. (This is a simple move since there’s nothing on top of it.)
- Step 2: The medium disk is moved from A to B.
- Step 3: The smallest disk is moved from C to B. (Now the top two disks have been moved to the auxiliary tower.)
- Step 4: The largest disk is moved from A to C. (This is the key move enabled by having the other disks out of the way.)
- Step 5: The smallest disk is moved from B to A.
- Step 6: The medium disk is moved from B to C. (Now the top two disks are back on the destination tower, but in the correct order.)
- Step 7: The smallest disk is moved from A to C.
End: All disks are stacked on tower C in the correct order.
Program to implement towers of Hanoi problem
def tower_of_hanoi(num_disks, source_peg, auxiliary_peg, destination_peg):
"""
Recursively solves the Tower of Hanoi problem.
Args:
num_disks: The number of disks to move.
source_peg: The peg from which to move the disks.
auxiliary_peg: The peg used as a temporary holding area.
destination_peg: The peg to which the disks are to be moved.
"""
if num_disks == 1:
# Base case: Only one disk left, move it directly to the destination.
print(f"Move disk 1 from peg {source_peg} to peg {destination_peg}")
return
# Recursive cases:
# 1. Move the top n-1 disks from the source peg to the auxiliary peg,
# using the destination peg as a temporary holder.
tower_of_hanoi(num_disks - 1, source_peg, destination_peg, auxiliary_peg)
# 2. Move the largest disk (the bottom one) from the source peg to the destination peg.
print(f"Move disk {num_disks} from peg {source_peg} to peg {destination_peg}")
# 3. Move the n-1 disks from the auxiliary peg to the destination peg,
# using the source peg as a temporary holder.
tower_of_hanoi(num_disks - 1, auxiliary_peg, source_peg, destination_peg)
# Example usage
num_disks = int(input("Enter the number of disks: "))
tower_of_hanoi(num_disks, 'A', 'B', 'C')
#include <iostream>
using namespace std;
void towerOfHanoi(int numDisks, char sourcePeg, char auxiliaryPeg, char destinationPeg) {
/*
* Recursively solves the Tower of Hanoi problem.
*
* Args:
* numDisks: The number of disks to move.
* sourcePeg: The peg from which to move the disks.
* auxiliaryPeg: The peg used as a temporary holding area.
* destinationPeg: The peg to which the disks are to be moved.
*/
if (numDisks == 1) {
// Base case: Move the single disk directly to destination.
cout << "Move disk 1 from peg " << sourcePeg << " to peg " << destinationPeg << endl;
return;
}
// Recursive steps:
// 1. Move the top n-1 disks from source to auxiliary (using destination as temp).
towerOfHanoi(numDisks - 1, sourcePeg, destinationPeg, auxiliaryPeg);
// 2. Move the largest disk (bottom) from source to destination.
cout << "Move disk " << numDisks << " from peg " << sourcePeg << " to peg " << destinationPeg << endl;
// 3. Move the n-1 disks from auxiliary to destination (using source as temp).
towerOfHanoi(numDisks - 1, auxiliaryPeg, sourcePeg, destinationPeg);
}
int main() {
int numDisks;
cout << "Enter the number of disks: ";
cin >> numDisks;
towerOfHanoi(numDisks, 'A', 'B', 'C'); // Start with pegs labeled A, B, C
return 0;
}
import java.util.Scanner;
public class TowerOfHanoi {
public static void towerOfHanoi(int numDisks, char sourcePeg, char auxiliaryPeg, char destinationPeg) {
/*
* Recursively solves the Tower of Hanoi problem.
*
* Args:
* numDisks: The number of disks to move.
* sourcePeg: The peg from which to move the disks.
* auxiliaryPeg: The peg used as a temporary holding area.
* destinationPeg: The peg to which the disks are to be moved.
*/
if (numDisks == 1) {
// Base case: Move the single disk directly to destination.
System.out.println("Move disk 1 from peg " + sourcePeg + " to peg " + destinationPeg);
return;
}
// Recursive steps:
// 1. Move the top n-1 disks from source to auxiliary (using destination as temp).
towerOfHanoi(numDisks - 1, sourcePeg, destinationPeg, auxiliaryPeg);
// 2. Move the largest disk (bottom) from source to destination.
System.out.println("Move disk " + numDisks + " from peg " + sourcePeg + " to peg " + destinationPeg);
// 3. Move the n-1 disks from auxiliary to destination (using source as temp).
towerOfHanoi(numDisks - 1, auxiliaryPeg, sourcePeg, destinationPeg);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter the number of disks: ");
int numDisks = scanner.nextInt();
towerOfHanoi(numDisks, 'A', 'B', 'C'); // Start with pegs labeled A, B, C
scanner.close(); // close the scanner after use
}
}
Output:
Enter the number of disks: 3
Move disk 1 from peg A to peg C
Move disk 2 from peg A to peg B
Move disk 1 from peg C to peg B
Move disk 3 from peg A to peg C
Move disk 1 from peg B to peg A
Move disk 2 from peg B to peg C
Move disk 1 from peg A to peg CFAQs On Tower of Hanoi
Q1. What are the rules of the Tower of Hanoi puzzle?
- Only one disk can be moved at a time.
- A disk can only be moved if it’s the top disk on a peg.
- No larger disk may be placed on top of a smaller disk.
Q2. Why is the Tower of Hanoi always solvable?
The puzzle is guaranteed to have a solution because the recursive algorithm used to solve it always breaks down the problem into smaller, solvable subproblems. As long as you follow the rules, you’ll eventually reach the solution.
Q3. What is the minimum number of moves to solve the Tower of Hanoi with n disks?
- The minimum number of moves is 2^n – 1.
- This means the complexity of the problem increases exponentially with the number of disks.
Q4.Is recursion necessary to solve the Tower of Hanoi?
- While recursion is the most elegant and common approach, it’s not strictly necessary.
- The puzzle can be solved using iterative algorithms as well, although they might be more complex to implement.
Q5. What are some real-world applications of the Tower of Hanoi?
- While not directly applicable to many real-world scenarios, the Tower of Hanoi serves as an excellent educational tool for understanding recursion and problem-solving strategies.
- It also has some indirect applications in areas like computer science (e.g., disk scheduling algorithms) and psychology (e.g., studying problem-solving skills).
