What is Stack?
- A stack is an implementation tool that is extensively used in programming languages. Stack is a linear data structure.
- A stack in data structure is an order list of elements where we can perform insertion and deletion at only one end.
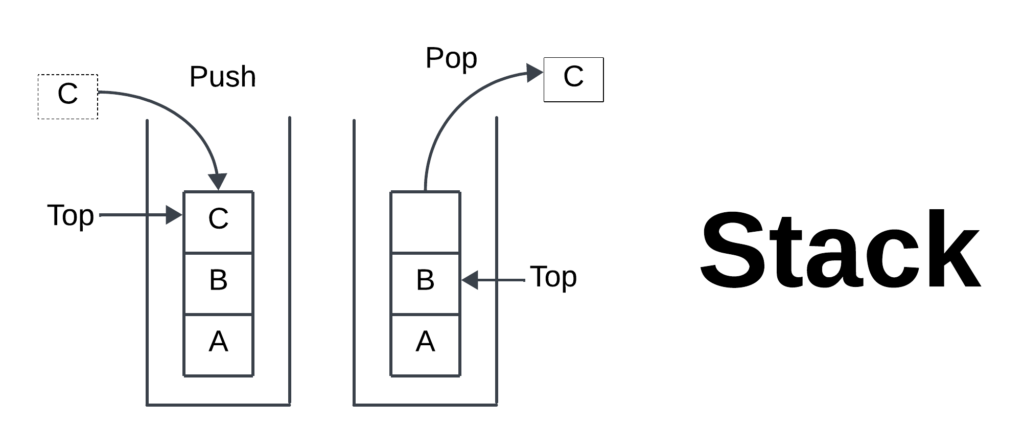
- Stacks operate on a “Last In, First Out” (LIFO) basis, where the most recently added element is the first to be removed.
- The major operations of the stack are PUSH and POP. PUSH means inserting an element into the stack. POP means deleting an element from the stack.
- Stack operations can be carried out through two distinct methods:
- Static Memory allocation.
- Dynamic Memory allocation.
- A stack is a linear data structure that can be implemented using a 1-D array when we use a 1-D array, a stack has a fixed number of values.
- We take the variable as a stack because all the operations at the stack can be performed at only one end. Initially, the value of the top is -1.
- Pushing an element onto the stack increases the top index by one.
- Performing a POP operation decreases the top index by one.
- The stack is unequivocally full when the top index reaches a value of MAX-1, indicating that all available slots are occupied.
- If the stack is full and if we try to perform a push operation, it results in a stack overflow.
- If the top value is -1, the stack is empty.
- If the stack is empty and we try to perform the POP operation it results in stack underflow.
Table of Contents
Basic Operations of a Stack
Stacks provide a range of operations for manipulating and organizing the data they hold.
- Push(): Used to insert an element into the stack.
- Pop(): Used to remove an element in the stack.
- Top() or Peek(): Used to know/check the top of the element in the stack
- isFull(): Used to check whether the stack is full.
- If it is full then return True else False.
- isEmpty(): Used to check whether the stack is empty or not
- If it is empty then return True else False.
Algorithm for Push() Operation:
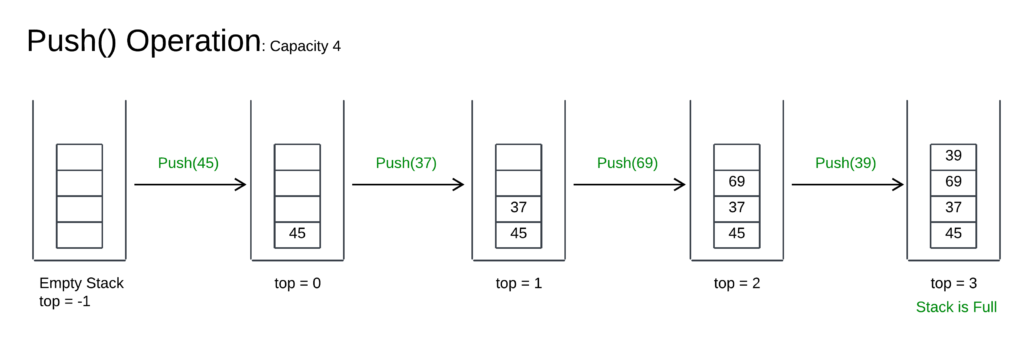
- Full Stack Check: Determine if the stack is full by comparing the top index to the maximum capacity. If the top equals capacity – 1, the stack is full.
- Handle Stack Overflow: If the stack is full, signal a “stack overflow” error to indicate that no further elements can be added.
- Increment Top Index: If the stack is not full, increment the top index by 1 to point to the next empty position.
- Insert Element: Store the new data element at the position indicated by the updated top index.
Algorithm for Pop() Operation:
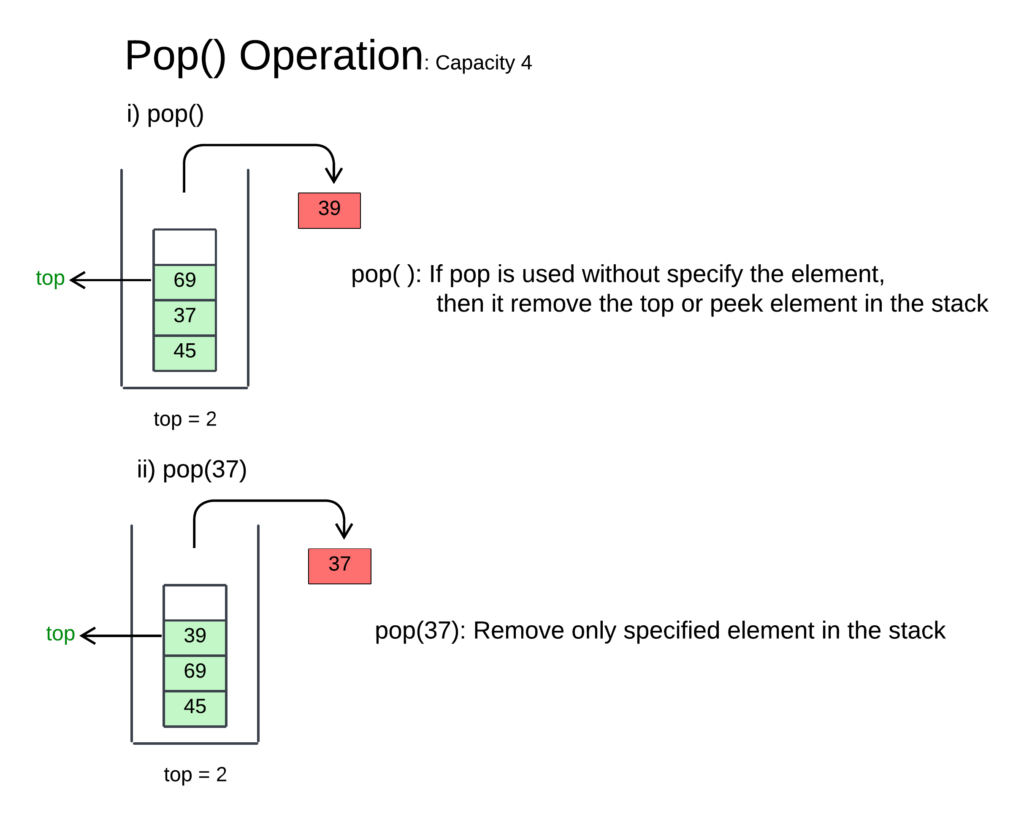
- Empty Stack Check: Determine if the stack is empty by checking if the top index is -1.
- Handle Stack Underflow: If the stack is empty, signal a “stack underflow” error to indicate that no items can be removed.
- Retrieve and Remove Top Item: If the stack is not empty, retrieve the item at the top index and store it temporarily.
- Decrement Top Index: Decrement the top index by 1 to point to the new top of the stack.
- Return Removed Item: Return the previously retrieved item as the result of the pop operation.
Algorithm for Top() or Peek() Operation:

- Empty Stack Check: Determine if the stack is empty by checking if the top index is -1.
- Handle Empty Stack: If the stack is empty, signal an error or return a specific value (e.g., null) to indicate that no top element exists.
- Return Top Element: If the stack is not empty, retrieve and return the element stored at the top index.
Algorithm for isFull() Operation:
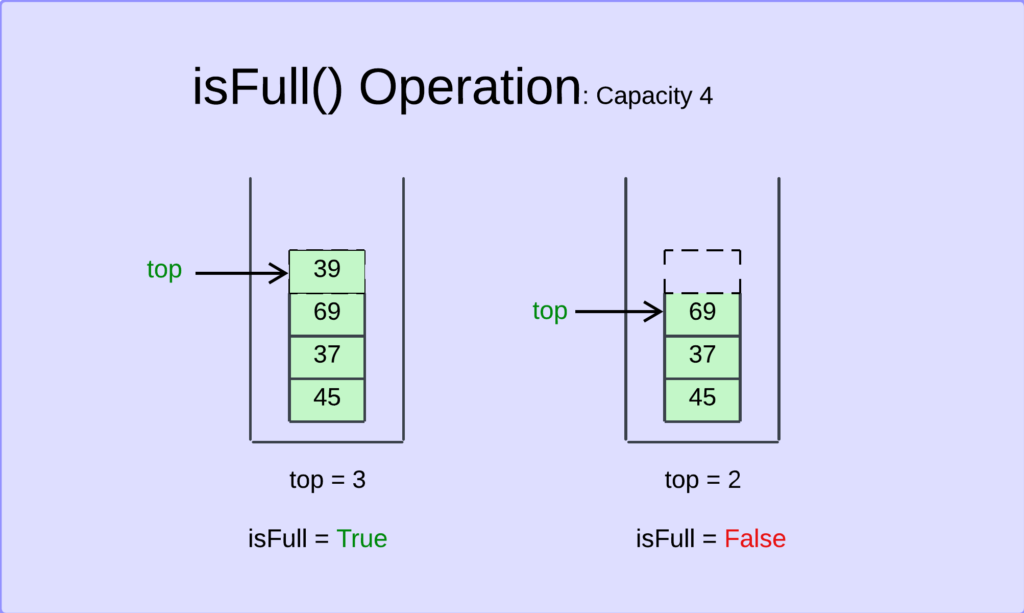
- Compare Top Index: Check if the top index is equal to capacity – 1.
- Determine Fullness:
- If the top index equals capacity – 1, the stack is full, and the function should return True.
- Otherwise, the stack is not full, and the function should return False.
Algorithm for isEmpty() Operation:
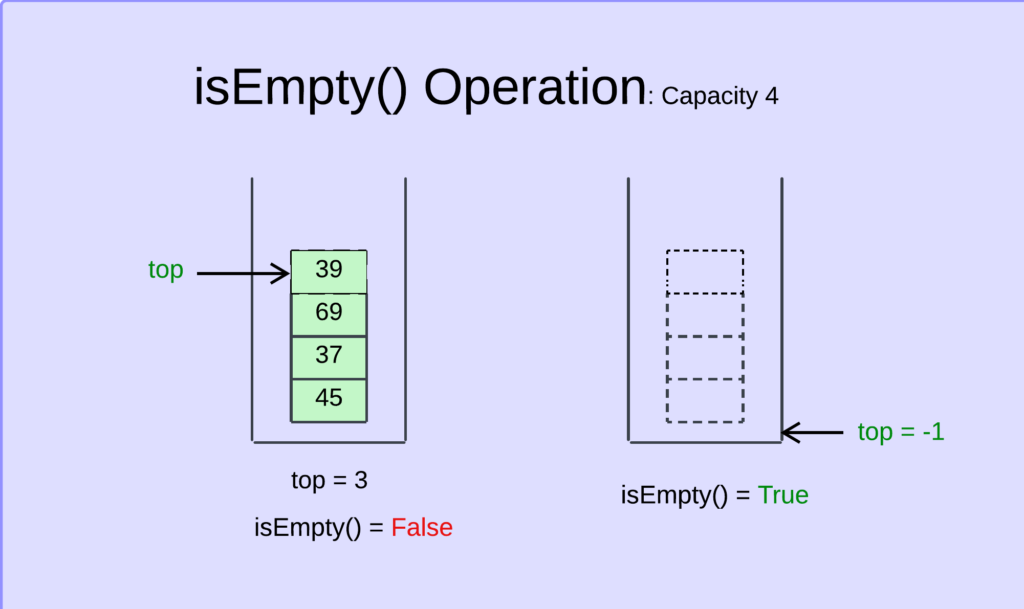
- Examine Top Index: Check if the top index is equal to -1.
- Determine Emptiness:
- If the top index equals -1, the stack is empty, and the function should return True.
- Otherwise, the stack is not empty, and the function should return False.
Implementation of a Stacks
Array-based Implementation
class Stack:
def __init__(self, max_size):
# Initialize an empty list to represent the stack
self.stack = []
# Store the maximum size of the stack
self.max_size = max_size
def push(self, data):
# Check if stack is full before pushing
if len(self.stack) == self.max_size:
print("Stack Overflow!")
return
# Add the element to the end of the list (top of the stack)
self.stack.append(data)
print(f"Pushed {data} onto the stack.")
def pop(self):
# Check if stack is empty before popping
if not self.stack:
print("Stack Underflow!")
return None
# Remove and return the last element (top of the stack)
popped_data = self.stack.pop()
print(f"Popped {popped_data} from the stack.")
return popped_data
def peek(self):
# Check if stack is empty
if not self.stack:
print("Stack is empty.")
return None
# Return the last element (top of the stack) without removing it
return self.stack[-1]
def is_empty(self):
# Check if the stack is empty
return not self.stack
# Example usage
stack = Stack(5) # Create a stack with a maximum size of 5
stack.push(10)
stack.push(20)
stack.push(30)
print(f"Top element: {stack.peek()}")
stack.pop()
print(f"Is stack empty? {stack.is_empty()}")
#include <iostream>
#include <vector>
using namespace std;
class Stack {
private:
vector<int> stack; // Dynamic array (vector) to store stack elements
int max_size; // Maximum allowed size of the stack
int top; // Index of the top element in the stack
public:
Stack(int max_size) : max_size(max_size), top(-1) {} // Constructor
void push(int data) {
// Check for stack overflow
if (top == max_size - 1) {
cout << "Stack Overflow!" << endl;
return;
}
// Increment top and add the element
stack.push_back(data);
top++;
cout << "Pushed " << data << " onto the stack." << endl;
}
int pop() {
// Check for stack underflow
if (top == -1) {
cout << "Stack Underflow!" << endl;
return -1; // Or some other error value
}
// Remove the top element
int popped_data = stack[top];
stack.pop_back(); // Reduce the size of the vector by 1.
top--;
cout << "Popped " << popped_data << " from the stack." << endl;
return popped_data;
}
int peek() {
// Check if the stack is empty
if (top == -1) {
cout << "Stack is empty." << endl;
return -1; // Or some other error value
}
// Return the top element without removing
return stack[top];
}
bool is_empty() {
// Check if the top index indicates an empty stack
return (top == -1);
}
};
int main() {
Stack stack(5); // Create a stack with a maximum size of 5
stack.push(10);
stack.push(20);
stack.push(30);
cout << "Top element: " << stack.peek() << endl;
stack.pop();
cout << "Is stack empty? " << stack.is_empty() << endl;
return 0;
}
import java.util.ArrayList;
import java.util.List;
class Stack {
private List<Integer> stack; // Use an ArrayList to dynamically store stack elements
private int maxSize; // Maximum allowed size of the stack
private int top; // Index of the top element in the stack
public Stack(int maxSize) {
this.maxSize = maxSize;
this.top = -1; // Initialize top to indicate an empty stack
this.stack = new ArrayList<>(maxSize); // Initialize the ArrayList with the specified capacity
}
public void push(int data) {
// Check for stack overflow
if (top == maxSize - 1) {
System.out.println("Stack Overflow!");
return;
}
// Increment top and add the element
top++;
stack.add(data); // Use add() method to append the element to the list
System.out.println("Pushed " + data + " onto the stack.");
}
public int pop() {
// Check for stack underflow
if (top == -1) {
System.out.println("Stack Underflow!");
return -1; // Or throw an exception
}
// Remove and return the top element
int poppedData = stack.get(top);
stack.remove(top); // Use remove() method to remove the element at the top index
top--;
System.out.println("Popped " + poppedData + " from the stack.");
return poppedData;
}
public int peek() {
// Check if the stack is empty
if (top == -1) {
System.out.println("Stack is empty.");
return -1; // Or throw an exception
}
// Return the top element without removing
return stack.get(top);
}
public boolean isEmpty() {
// Check if the top index indicates an empty stack
return (top == -1);
}
public static void main(String[] args) {
Stack stack = new Stack(5); // Create a stack with a maximum size of 5
stack.push(10);
stack.push(20);
stack.push(30);
System.out.println("Top element: " + stack.peek());
stack.pop();
System.out.println("Is stack empty? " + stack.isEmpty());
}
}
#include <stdio.h>
#include <stdbool.h>
#define MAX_SIZE 100 // Maximum stack size (you can adjust this)
typedef struct {
int data[MAX_SIZE]; // Array to store stack elements
int top; // Index of the top element
} Stack;
// Function to initialize an empty stack
void initializeStack(Stack* stack) {
stack->top = -1; // Initialize top to -1 to indicate an empty stack
}
// Function to push an element onto the stack
void push(Stack* stack, int data) {
// Check for stack overflow
if (stack->top == MAX_SIZE - 1) {
printf("Stack Overflow!\n");
return;
}
// Increment top and add the element
stack->top++;
stack->data[stack->top] = data;
printf("Pushed %d onto the stack.\n", data);
}
// Function to pop an element from the stack
int pop(Stack* stack) {
// Check for stack underflow
if (stack->top == -1) {
printf("Stack Underflow!\n");
return -1; // Or some other error value
}
// Retrieve the top element, decrement top, and return the element
int poppedData = stack->data[stack->top];
stack->top--;
printf("Popped %d from the stack.\n", poppedData);
return poppedData;
}
// Function to peek at the top element without removing it
int peek(Stack* stack) {
// Check if the stack is empty
if (stack->top == -1) {
printf("Stack is empty.\n");
return -1; // Or some other error value
}
// Return the top element
return stack->data[stack->top];
}
// Function to check if the stack is empty
bool isEmpty(Stack* stack) {
return (stack->top == -1);
}
int main() {
Stack stack;
initializeStack(&stack); // Initialize the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
printf("Top element: %d\n", peek(&stack));
pop(&stack);
printf("Is stack empty? %s\n", isEmpty(&stack) ? "true" : "false");
return 0;
}
Output:
Pushed 10 onto the stack.
Pushed 20 onto the stack.
Pushed 30 onto the stack.
Top element: 30
Popped 30 from the stack.
Is stack empty? FalseAdvantages of using Array-based Stacks:
- Simple implementation with basic array manipulation.
- Efficient push and pop operations (O(1)).
- Cache-friendly due to contiguous memory storage.
- Predictable memory usage for easier management.
- Ideal for fixed-size stacks with known maximum size.
Disadvantages of using Array-based Stacks:
- Fixed capacity leads to potential stack overflow.
- Inefficient resizing with O(n) time complexity.
- Wasted space due to underutilized stack.
- Less flexible for scenarios with unknown or varying maximum sizes.
- Implementation overhead for overflow handling
Linked List-based Implementation
class Node:
def __init__(self, data):
# Data stored in the node
self.data = data
# Pointer to the next node in the stack (initially None)
self.next = None
class Stack:
def __init__(self):
# Initialize an empty stack (head points to None)
self.head = None
def push(self, data):
# Create a new node to hold the data
new_node = Node(data)
# Check if the stack is empty
if self.head is None:
# If empty, make the new node the head
self.head = new_node
else:
# Otherwise, link the new node to the current head
new_node.next = self.head
# Update the head to the new node
self.head = new_node
def pop(self):
# Check if the stack is empty
if self.head is None:
return None # or raise an exception
# Store the data to be popped
popped_data = self.head.data
# Update the head to the next node in the stack
self.head = self.head.next
return popped_data
def peek(self):
# Check if the stack is empty
if self.head is None:
return None # or raise an exception
# Return the data of the head node (top of the stack)
return self.head.data
def is_empty(self):
# Check if the head is None (indicating an empty stack)
return self.head is None
# Example usage
stack = Stack()
stack.push(10)
stack.push(20)
stack.push(30)
print(f"Top element: {stack.peek()}")
print(f"Popped: {stack.pop()}")
print(f"Is stack empty? {stack.is_empty()}")
#include <iostream>
using namespace std;
// Node structure to represent a single element of the stack
struct Node {
int data;
Node* next;
Node(int data) : data(data), next(nullptr) {} // Constructor
};
class Stack {
private:
Node* top; // Pointer to the top of the stack
public:
Stack() : top(nullptr) {} // Constructor - initializes an empty stack
void push(int data) {
// Create a new node
Node* new_node = new Node(data);
// Check if the stack is empty
if (top == nullptr) {
// If empty, make the new node the top
top = new_node;
} else {
// Otherwise, link the new node to the current top
new_node->next = top;
// Update the top pointer
top = new_node;
}
}
int pop() {
// Check if the stack is empty
if (top == nullptr) {
cout << "Stack Underflow!" << endl;
return -1; // Or throw an exception
}
// Get the data from the top node
int popped_data = top->data;
// Store the top node to be deleted
Node* temp = top;
// Update the top pointer to the next node
top = top->next;
// Delete the old top node
delete temp;
return popped_data;
}
int peek() {
// Check if the stack is empty
if (top == nullptr) {
cout << "Stack is empty." << endl;
return -1; // Or throw an exception
}
// Return the data of the top node
return top->data;
}
bool is_empty() {
// Check if the top pointer is null (indicating an empty stack)
return (top == nullptr);
}
};
int main() {
Stack stack;
stack.push(10);
stack.push(20);
stack.push(30);
cout << "Top element: " << stack.peek() << endl;
cout << "Popped: " << stack.pop() << endl;
cout << "Is stack empty? " << stack.is_empty() << endl;
return 0;
}
class Node {
int data; // Data stored in the node
Node next; // Reference to the next node
// Constructor
public Node(int data) {
this.data = data;
this.next = null; // Initially, the next node is null
}
}
class Stack {
private Node top; // Reference to the top node of the stack
// Constructor - initializes an empty stack
public Stack() {
top = null;
}
public void push(int data) {
// Create a new node
Node newNode = new Node(data);
// If the stack is empty, make the new node the top
if (top == null) {
top = newNode;
} else {
// Otherwise, link the new node to the current top
newNode.next = top;
// Update the top reference
top = newNode;
}
}
public int pop() {
// Check for stack underflow
if (top == null) {
System.out.println("Stack Underflow!");
return -1; // Or throw an exception
}
// Store the data to be popped
int poppedData = top.data;
// Update the top reference to the next node
top = top.next;
return poppedData;
}
public int peek() {
// Check if the stack is empty
if (top == null) {
System.out.println("Stack is empty.");
return -1; // Or throw an exception
}
// Return the data of the top node
return top.data;
}
public boolean isEmpty() {
// Check if the top reference is null (indicating an empty stack)
return (top == null);
}
public static void main(String[] args) {
Stack stack = new Stack();
stack.push(10);
stack.push(20);
stack.push(30);
System.out.println("Top element: " + stack.peek());
System.out.println("Popped: " + stack.pop());
System.out.println("Is stack empty? " + stack.isEmpty());
}
}
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// Node structure to represent a single element in the stack
struct Node {
int data;
struct Node* next;
};
// Stack structure
typedef struct {
struct Node* top;
} Stack;
// Function to initialize an empty stack
void initializeStack(Stack* stack) {
stack->top = NULL; // Start with an empty stack
}
// Function to push an element onto the stack
void push(Stack* stack, int data) {
// Create a new node
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
new_node->data = data;
new_node->next = NULL;
// Check if the stack is empty
if (stack->top == NULL) {
// If empty, set the new node as the top
stack->top = new_node;
} else {
// Otherwise, insert the new node at the beginning (top)
new_node->next = stack->top;
stack->top = new_node;
}
}
// Function to pop an element from the stack
int pop(Stack* stack) {
// Check for stack underflow
if (stack->top == NULL) {
printf("Stack Underflow!\n");
return -1; // Or throw an exception
}
// Store the top node
struct Node* temp = stack->top;
// Retrieve the data, move the top to the next node, and free the old top
int popped_data = temp->data;
stack->top = temp->next;
free(temp);
return popped_data;
}
// Function to peek at the top element
int peek(Stack* stack) {
// Check if the stack is empty
if (stack->top == NULL) {
printf("Stack is empty.\n");
return -1; // Or throw an exception
}
// Return the data of the top node
return stack->top->data;
}
// Function to check if the stack is empty
bool is_empty(Stack* stack) {
return (stack->top == NULL);
}
int main() {
Stack stack;
initializeStack(&stack);
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
printf("Top element: %d\n", peek(&stack));
printf("Popped: %d\n", pop(&stack));
printf("Is stack empty? %s\n", is_empty(&stack) ? "true" : "false");
return 0;
}
Output:
Top element: 30
Popped: 30
Is stack empty? FalseAdvantages of using Linked List-based Sacks
- Linked list-based stacks dynamically grow or shrink, reducing overflow risk.
- Memory is allocated only for needed elements, optimizing usage.
- Unlike array-based stacks, they consume memory proportional to elements.
Disadvantages of using Linked List-based Stacks
- Increased memory overhead due to pointers.
- Slower random access due to traversal.
- More complex implementation involving nodes and pointers.
Time and Space Complexity of Stack Operations
| Operation | Time Complexity | Space Complexity |
| Push | O(1) | O(n) |
| Pop | O(1) | O(n) |
| Top | O(1) | O(n) |
| IsEmpty | O(1) | O(n) |
| IsFull | O(1) | O(n) |
Explanation:
- Time Complexity:
- Push, Pop, Top, IsEmpty, and IsFull operations all take constant time (O(1)) because they only involve accessing or modifying the top element of the stack.
- Space Complexity:
- The space complexity of a stack depends on the number of elements (n). Pushing an element increases space by 1 while popping decreases it by 1.
Application of Stack in Data Structure
Stacks can be involved in major applications. Stacks can be easily applied to get a simple and efficient solution. The major applications of the stacks are
- Reversing the given list
- Converting the decimal number into its binary equivalent
- Recursion
- Towers of Hanoi
- Parenthesis checker
- Transforming an infixed expression into both postfix and prefix notations.
- Determining the value of an expression in postfix or prefix notation.
Conclusion
Stacks are versatile data structures that follow the LIFO principle. They are crucial in computer science and have many applications. Understanding stack operations and their implementation is essential. Familiarity with stack-related concepts can enhance technical interview and academic performance.
Frequently Asked Questions(FAQs) in Interview and Academics
1. What is a Stack and What Principle Does It Follow?
- A stack is a linear data structure adhering to the Last-In-First-Out (LIFO) principle. This means the last element added (pushed) is the first one removed (popped).
2. How Can You Implement a Stack?
Stacks can be implemented using:
- Arrays: Simple and efficient for fixed-size stacks.
- Linked Lists: More flexible for dynamically sized stacks.
3. What are the Common Applications of Stacks?
- Function Calls: Tracking the order of function execution.
- Undo/Redo Functionality: Storing previous states.
- Expression Evaluation: Evaluating mathematical expressions using postfix/prefix notation.
- Backtracking Algorithms: Exploring solution spaces.
- Browser History: Keeping track of visited pages.
4. Explain How to Reverse a String Using a Stack.
- Push each character of the string onto the stack.
- Remove characters from the stack individually and sequentially add them to a new string.
- The new string will be the reversed version of the original.
Code Example (Python):
def reverse_string(input_str):
stack = []
for char in input_str:
stack.append(char)
reversed_str = “”
while stack:
reversed_str += stack.pop()
return reversed_str
5. How Do You Handle Stack Overflow and Underflow?
- Stack Overflow: Handle using a dynamically sized implementation, throwing an exception, or resizing the array-based stack.
- Stack Underflow: Handle by throwing an exception or returning a special value.
6. How Would You Design a Min Stack (a Stack That Can Retrieve the Minimum Element in O(1) Time)?
You can achieve this by maintaining two stacks:
- Main Stack: Stores the regular elements.
- Min Stack: Stores the minimum element encountered so far.
When pushing an element:
- Push it onto the main stack.
- If the min stack is empty or the element is smaller than or equal to the top of the min stack, push it onto the min stack as well.
When popping an element:
- Pop from the main stack.
- If the popped element is equal to the top of the min stack, pop from the min stack as well.
The top of the min stack always holds the current minimum element. Maintain two stacks:
- Main stack: stores regular elements.
- Min stack: stores the minimum element encountered.
When pushing an element:
- Push it onto the main stack.
- If the min stack is empty or the element is smaller or equal, push it onto the min stack.
When popping an element:
- Pop from the main stack.
- If the popped element equals the top of the min stack, pop from the min stack.
The top of the min stack always holds the current minimum element.
7. Can You Implement a Queue Using Two Stacks?
Yes! This is a classic interview question. Here’s the approach:
- Enqueue: Push the new element onto stack1.
- Dequeue:
- If stack2 is not empty, pop from stack2.
- If stack2 is empty, transfer all elements from stack1 to stack2 (reversing their order) and then pop from stack2.
8. How Can You Sort a Stack Using Only Stack Operations (No Additional Data Structures)?
This involves a recursive approach:
- Pop an element from the input stack.
- Recursively sort the remaining stack.
- Insert the popped element back into the sorted stack in the correct position.
