Spanning Tree – MST, Kruskal’s and Prim’s Algorithms 

Introduction to Spanning Tree

• A spanning tree of a connected, undirected graph is a tree that connects all the vertices of the graph without any cycles. 
• A single graph can have multiple spanning trees. Spanning trees are essential because they provide a minimal, connected representation of the original graph, which is useful for various applications, such as network design and routing.
• While a spanning tree does involve a subset of edges, it’s more accurately described as a “subgraph” since it retains the vertices.

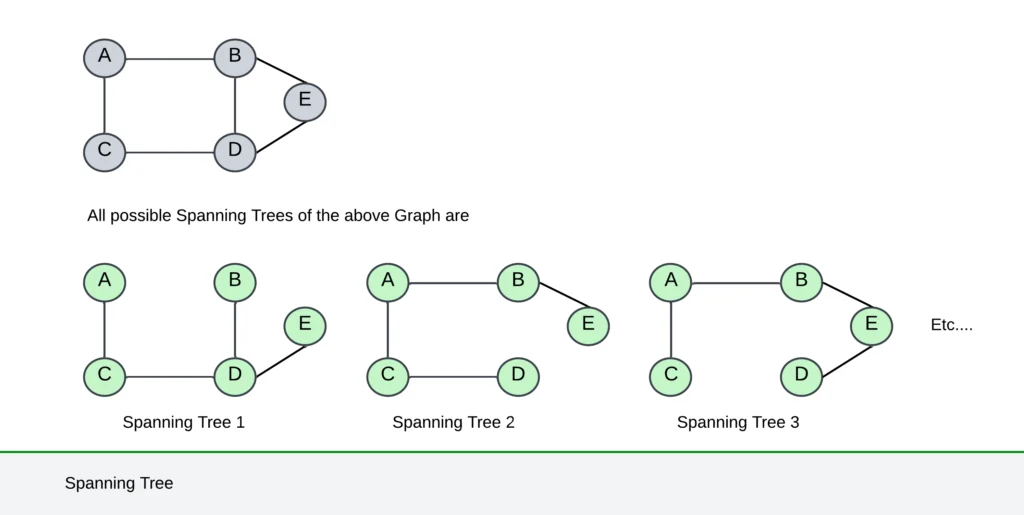
Note: A complete undirected graph can have a maximum n^n-2 number of spanning trees where n is the list of nodes.

General properties of a spanning tree:

1. A connected graph G can have more than one spanning tree.
2. All possible spanning trees of a graph G have the same number of edges and vertices.
3. The spanning tree does not have a cycle.
4. Removing any single edge from a spanning tree will disconnect the graph, splitting it into two components.
5. Adding the edge to a spanning tree will create a circuit or a loop.

Applications of Spanning Tree:

The Spanning Tree is used to find the minimum part to connect all the nodes in graph G.

The applications are

1. Civil Network Planning
2. Computer network routing protocol
3. Cluster analysis.

Minimum Spanning Tree (MST):

What is a Minimum Spanning Tree (MST)?

• When a graph has weighted edges, the Minimum Spanning Tree (MST) is a spanning tree that achieves the lowest possible total weight for its edges, making it the most efficient way to connect all vertices.
• In other words, it connects all the vertices of the graph without any cycles, and the sum of the weights of the edges in the MST is the lowest possible. 
• MSTs are important for optimizing networks, finding the least expensive way to connect points, and clustering algorithms.

In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all the other spanning trees of the same graph G. The two important algorithms to construct a minimum spanning tree are

1. Kruskal’s Algorithm
2. Prim’s Algorithm

Both these are greedy algorithms.

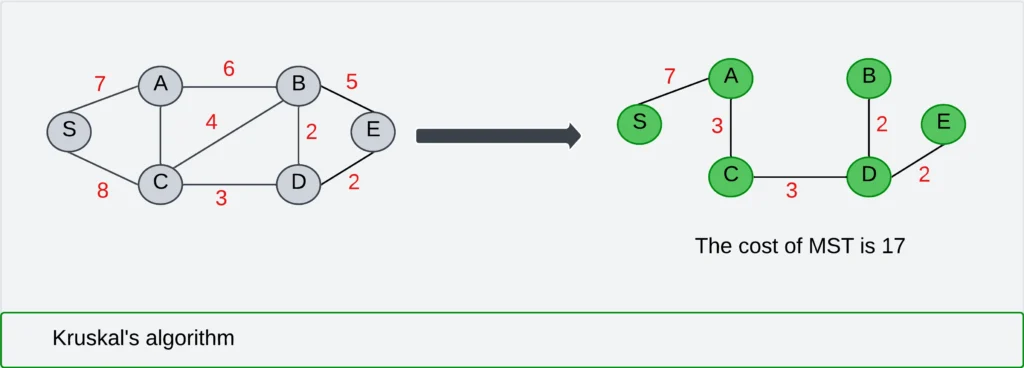
1. Kruskal’s Algorithm: 

• To construct a minimum spanning tree we have to follow the following steps.
  1. Eliminate all loops and parallel edges, preserving only the lowest-cost edge for any pair of vertices with multiple connections.
  2. Arrange all the edges in the increasing order of the weights.
  3. Add the edge which has the least weight.

Note: we ignore the edge that will create a circuit or loop.

Consider the following example.

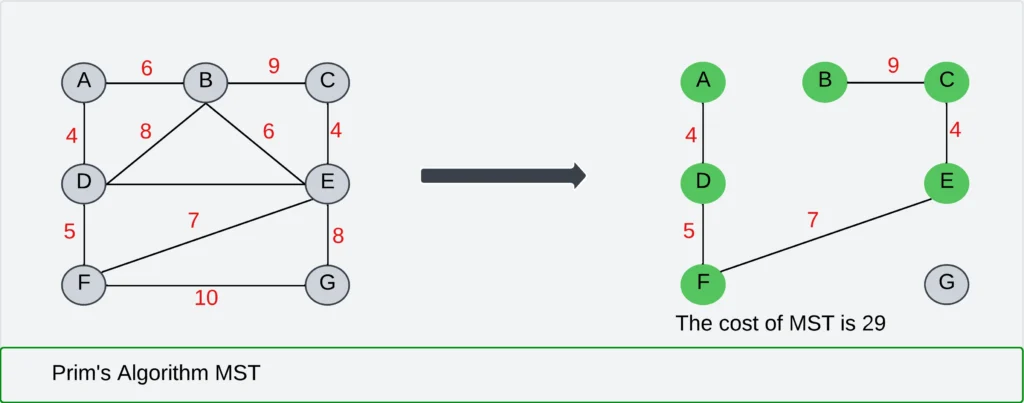
2. Prim’s Algorithm: 

• Simplify the graph by removing loops and redundant connections (parallel edges). When encountering parallel edges, retain only the edge with the minimal associated cost.
  1. Eliminate all loops and parallel edges, preserving only the lowest-cost edge for any pair of vertices with multiple connections.
  2. Choose an arbitrary node as the root node.
  3. Look at all the paths leading out from this point and pick the cheapest to travel.

Note: we ignore the edge that will create a loop or circuit.

Related FAQs:

1. Which algorithms are commonly employed to determine the Minimum Spanning Tree of a graph?

Two popular algorithms are used to find the Minimum Spanning Tree of a graph:

• Prim’s Algorithm: This algorithm starts with a single vertex and iteratively adds the edge with the minimum weight connecting a vertex in the MST to a vertex outside the MST until all vertices are included.
• Kruskal’s Algorithm: This algorithm considers edges in increasing order of their weights. It adds an edge to the MST if it doesn’t create a cycle and connects two disjoint sets of vertices, continuing until all vertices are connected.

2. What are some real-world applications of Minimum Spanning Trees?

MSTs are valuable for optimizing connections and minimizing costs:

• Network Design: Finding the least expensive way to connect computers in a network or lay cables in a new neighborhood.
• Cluster Analysis: Grouping similar data points based on distances or similarities, where the MST can help identify clusters.
• Image Segmentation: Dividing an image into meaningful regions based on pixel similarities, with the MST helping define boundaries.
• Approximations for Traveling Salesperson Problem: While not providing the optimal solution, MSTs can be used to find approximate solutions to the Traveling Salesperson Problem.

3. How do I choose between Prim’s and Kruskal’s algorithms for my application?

The choice between Prim’s and Kruskal’s algorithms often depends on the graph’s structure and the implementation’s efficiency:

• Dense Graphs: Prim’s algorithm tends to be faster for dense graphs ( with many edges relative to the number of vertices) as it focuses on finding the minimum edge from a growing tree.
• Sparse Graphs: Kruskal’s algorithm can be more efficient for sparse graphs (fewer edges) because it sorts the edges once at the beginning and then iterates through them.
• Implementation: The efficiency also depends on the data structures used to implement the algorithms (e.g., using a Fibonacci heap for Prim’s algorithm can improve its time complexity).

4. What is the time complexity of Prim’s and Kruskal’s algorithms?

The time complexity of both Prim’s and Kruskal’s algorithms depends on the data structures used in their implementation.

• Prim’s Algorithm: Using a simple adjacency matrix and a priority queue, Prim’s algorithm has a time complexity of O(V^2), where V is the number of vertices. Using a Fibonacci heap for the priority queue can improve this to O(E + V log V), where E is the number of edges, making it efficient for dense graphs.
• Kruskal’s Algorithm: The dominant operation in Kruskal’s algorithm is sorting the edges, which takes O(E log E) time. With an efficient implementation of the disjoint-set data structure for cycle detection, the overall time complexity becomes O(E log E) or O(E log V) (since E is at most V^2).

5. Can a disconnected graph have a spanning tree?

• No, a disconnected graph cannot have a spanning tree. 
• A spanning tree, by definition, must connect all vertices of a graph into a single connected component without cycles. 
• If a graph is disconnected, it means there are at least two sets of vertices that are not reachable from each other, making it impossible to create a single tree that spans all vertices.

6. Is the Minimum Spanning Tree of a graph always unique?

• Not necessarily. A graph can have multiple Minimum Spanning Trees if considerable sets of edges result in the same minimum total edge weight. 
• For instance, if a graph has multiple edges with the same minimum weight, different MSTs can be formed by choosing various combinations of these edges. 
• However, even if the MST is not unique, the minimum total edge weight will be the same for all possible MSTs of that graph.