Shell Sort Algorithm – Data Structure

/ Data Structures, Sorting Techniques / By

What is Shell Sort?

Shell sort is the generalization of the insertion sort invented by Donald Shell in 1959. Shell sort is a highly efficient sorting technique. Shell sort is also called diminishing increment sort. In insertion sort, we observe two things

  1. It works very well when the data is almost sorted.
  2. It could be more efficient as it moves the values in one position at a time.

Shell sort is an improvement over insertion sort as it compares the elements by a gap of several positions. This enables the elements to take bigger steps toward their expected position. 

In these sorting, elements are stored in multiple passes; in each pass, data is taken with smaller and smaller gap sizes. The standard gap size for shell sort is n/2, n/4, n/8, n/16. However, the last gap size of the shell sort is the insertion sort. 

By this time we reach the last gap size the elements are almost in sorted order and hence it gives good performance.

Shell Short Algorithm

Algorithm Steps:

  1. Calculate Initial Gap: Start with a gap roughly half the array size.
  2. Divide and Sort Subarrays: Split the array into subarrays based on the gap and sort each subarray using insertion sort.
  3. Reduce the Gap: Decrease the gap size iteratively (e.g., by dividing it by 2).
  4. Repeat Steps 2 and 3: Continue sorting with reduced gaps until the gap becomes 
  5. Final Insertion Sort: Perform a final insertion sort on the entire array to guarantee complete order.

Working of Shell Sort with an example

The Shell Sort algorithm applied to the example array [15, 20, 10, 30, 50, 18, 5, 45], along with the logic in each step:

Step 1: Calculate Initial Gap:

  • Often, the initial gap is half the array size. Here, the gap starts as 8 / 2 = 4.

Step 2: Create Subarrays and Sort:

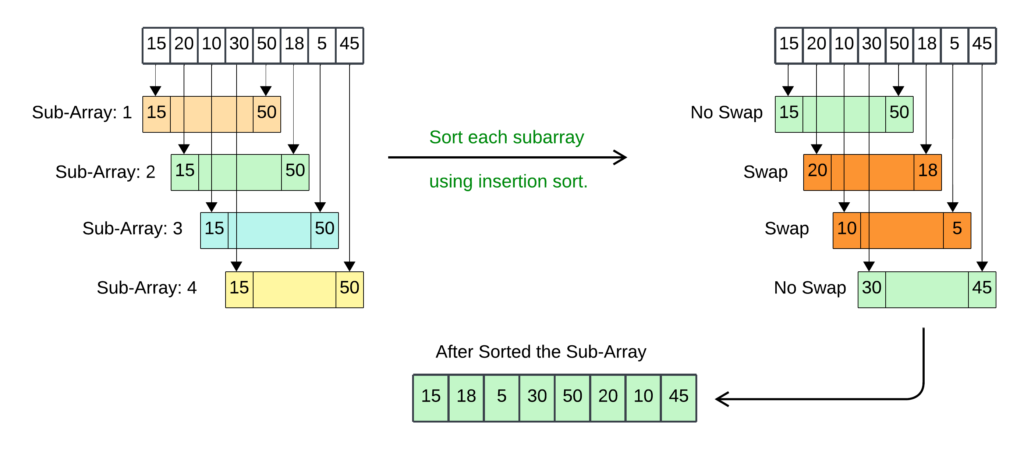
shell sort
  • Divide the array into subarrays based on the gap.
    • Subarray 1: [15, 50]
    • Subarray 2: [20, 18]
    • Subarray 3: [10, 5]
    • Subarray 4: [30, 45]
  • Sort each subarray using insertion sort.
    • After sorting: [15, 50], [18, 20], [5, 10], [30, 45]
  • Array after sorting the gap 4 : [15, 18, 5, 30, 50, 20, 10, 45]

Step 3: Reduce Gap

  • Reduce the gap. A common practice is to divide the gap by 2. New gap: 4 / 2 = 2.

Step 4: Create New Subarrays and Sort:

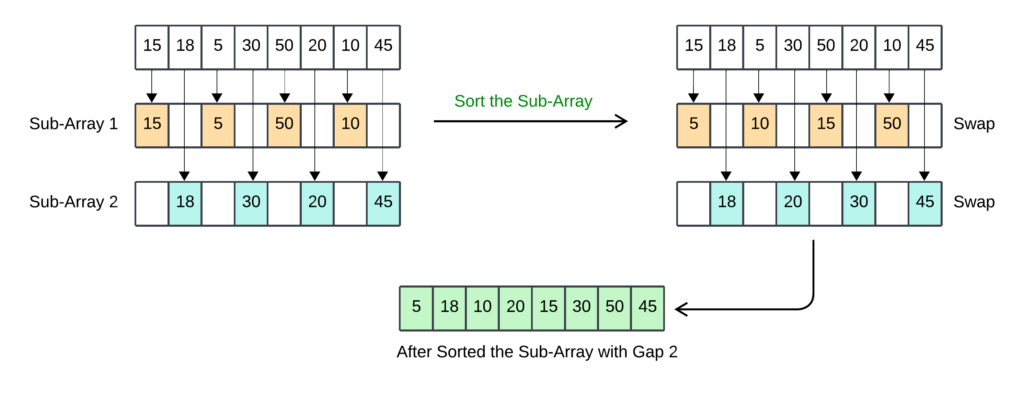
shell sort with gap 2
  • Divide the array again based on the new gap.
    • Subarray 1: [15, 5, 50, 10]
    • Subarray 2: [18, 30, 20, 45]
  • Sort each subarray.
    • After sorting: [5, 10, 15, 50], [18, 20, 30, 45].
  • Array after Step 4: [5, 18, 10, 20, 15, 30, 50, 45]

Step 5: Reduce Gap Again:

  • The gap becomes 2 / 2 = 1.

Step 6: Final Insertion Sort:

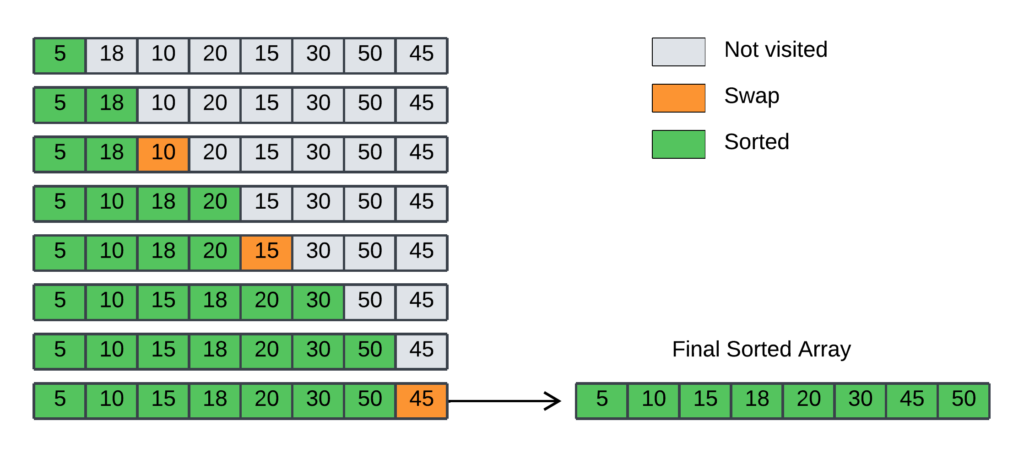
shell sort with gap 1
  • With a gap of 1, the entire array is now a single subarray. Perform a final insertion sort fully to ensure it’s fully sorted.
  • After sorting: [5, 10, 15, 18, 20, 30, 45, 50]

Shell Sort Program Implementation

def shell_sort(arr):
    n = len(arr)
    gap = n // 2
    # Continue while the gap is greater than 0
    while gap > 0:
        print(f"\nGap: {gap}")
        # Iterate over the array starting from the gap position
        for i in range(gap, n):
            temp = arr[i]  # Store the current element as a temporary value
            # Find the correct position for the current element
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]  # Shift elements if they are larger than temp
                j -= gap
            arr[j] = temp  # Insert the current element at its correct position
        print(f"After sorting with gap {gap}: {arr}")  # Print the array after sorting with this gap
        gap //= 2  # Reduce the gap for the next iteration
# Example usage
data = [15, 20, 10, 30, 50, 18, 5, 45]
print(f"Original array: {data}")
shell_sort(data)
print(f"\nFinal sorted array: {data}")

#include <iostream>
#include <vector>
using namespace std;
void shellSort(vector<int>& arr) {
    int n = arr.size();
    int gap = n / 2;
    // Continue while the gap is greater than 0
    while (gap > 0) {
        cout << "\nGap: " << gap << endl;
        // Iterate over the array starting from the gap position
        for (int i = gap; i < n; i++) {
            int temp = arr[i];  // Store the current element as a temporary value
            // Find the correct position for the current element
            int j = i;
            while (j >= gap && arr[j - gap] > temp) {
                arr[j] = arr[j - gap]; // Shift elements if they are larger than temp
                j -= gap;
            }
            arr[j] = temp; // Insert the current element at its correct position
        }
        // Print the array after sorting with this gap
        cout << "After sorting with gap " << gap << ": ";
        for (int num : arr) {
            cout << num << " ";
        }
        cout << endl;
        gap /= 2; // Reduce the gap for the next iteration
    }
}
int main() {
    vector<int> data = {15, 20, 10, 30, 50, 18, 5, 45};
    cout << "Original array: ";
    for (int num : data) {
        cout << num << " ";
    }
    cout << endl;
    shellSort(data);
    cout << "\nFinal sorted array: ";
    for (int num : data) {
        cout << num << " ";
    }
    cout << endl;
    return 0;
}

import java.util.Arrays;
public class ShellSort {
    public static void shellSort(int[] arr) {
        int n = arr.length;
        int gap = n / 2;
        // Continue while the gap is greater than 0
        while (gap > 0) {
            System.out.println("\nGap: " + gap);
            // Iterate over the array starting from the gap position
            for (int i = gap; i < n; i++) {
                int temp = arr[i]; // Store the current element as a temporary value
                // Find the correct position for the current element
                int j = i;
                while (j >= gap && arr[j - gap] > temp) {
                    arr[j] = arr[j - gap]; // Shift elements if they are larger than temp
                    j -= gap;
                }
                arr[j] = temp; // Insert the current element at its correct position
            }
            // Print the array after sorting with this gap
            System.out.println("After sorting with gap " + gap + ": " + Arrays.toString(arr)); 
            gap /= 2; // Reduce the gap for the next iteration
        }
    }
    public static void main(String[] args) {
        int[] data = {15, 20, 10, 30, 50, 18, 5, 45};
        System.out.println("Original array: " + Arrays.toString(data));
        shellSort(data);
        System.out.println("\nFinal sorted array: " + Arrays.toString(data));
    }
}

#include <stdio.h>
void shellSort(int arr[], int n) {
    int gap, i, j, temp;
    // Continue while the gap is greater than 0
    for (gap = n / 2; gap > 0; gap /= 2) {
        printf("\nGap: %d\n", gap);
        // Iterate over the array starting from the gap position
        for (i = gap; i < n; i++) {
            temp = arr[i]; // Store the current element as a temporary value
            // Find the correct position for the current element
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap]; // Shift elements if they are larger than temp
            }
            arr[j] = temp; // Insert the current element at its correct position
        }
        // Print the array after sorting with this gap
        printf("After sorting with gap %d: ", gap);
        for (j = 0; j < n; j++) {
            printf("%d ", arr[j]);
        }
        printf("\n");
    }
}
int main() {
    int data[] = {15, 20, 10, 30, 50, 18, 5, 45};
    int n = sizeof(data) / sizeof(data[0]); // Calculate the number of elements
    printf("Original array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", data[i]);
    }
    printf("\n");
    shellSort(data, n);
    printf("\nFinal sorted array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", data[i]);
    }
    printf("\n");
    return 0;
}

Output:

Original array: [15, 20, 10, 30, 50, 18, 5, 45]
Gap: 4
After sorting with gap 4: [15, 18, 5, 30, 50, 20, 10, 45]
Gap: 2
After sorting with gap 2: [5, 18, 10, 20, 15, 30, 50, 45]
Gap: 1
After sorting with gap 1: [5, 10, 15, 18, 20, 30, 45, 50]
Final sorted array: [5, 10, 15, 18, 20, 30, 45, 50]

Shell Sort Complexity Analysis(Time, Auxiliary, Space)

ComplexityTime ComplexityAuxiliary SpaceSpace Complexity
AverageO(n log n)O(1)O(n)
BestO(n)O(1)O(n)
WorstO(n^2)O(1)O(n)

Advantages and Disadvantages of Shell Sort

Advantages

  1. Faster for Medium Data: Efficient for medium-sized datasets compared to basic sorts like insertion and bubble sort.
  2. Adaptable Gaps: Flexible with gap sequences to optimize for specific data.
  3. Simple to Implement: Easy to understand and code.
  4. Memory-Efficient: Sorts in place, using minimal extra memory.
  5. Good for Almost Sorted Data: Efficient for data that’s already partially sorted.

Disadvantages

  1. Slower for Large Data: Less efficient than quicksort or merge sort for largest datasets.
  2. Complex Analysis: Average-case time complexity depends on the gap sequence.
  3. Unstable Sorting: May change the order of equal elements.
  4. Worst-Case Performance: Can degrade to O(n^2) in the worst case.
  5. Gap Sequence Matters: Choosing the right gap sequence is crucial for performance.

Q1. What are some real-world applications where Shell Sort might be a suitable choice?

  • Shell Sort can be a good choice for sorting moderately sized datasets Whenever memory is limited. It’s also useful when you have a good reason to believe the data is mostly sorted and you want to take advantage of its adaptive behavior. 
  • Some specific applications include embedded systems with limited memory and situations When it is essential to a quick sorting solution without requiring complex algorithms like quicksort or merge sort.

Q2. Can you provide some tips for optimizing Shell Sort’s performance?

  • The selection of the gap sequence plays a pivotal role in optimizing the performance of Shell Sort.
  • Experimenting with different sequences (e.g., Knuth’s or Hibbard’s) can lead to significant improvements. 
  • To further optimize Shell Sort, consider leveraging alternative sorting algorithms to enhance the efficiency of the subarray sorting phase.

Q3. How does Shell Sort compare to other sorting algorithms like quicksort and merge sort?

  • Shell Sort performs well for medium-sized datasets but can be less efficient than quicksort or merge sort for large datasets. 
  • The average-case performance of both Quicksort and merge sort, with a time complexity of O(n log n), is unequivocally superior to Shell Sort’s best-case performance in theoretical terms.
  • However, Shell Sort’s in-place nature and simplicity can make it a preferable choice in certain situations, especially when memory constraints are a factor.

Q4. Is Shell Sort a stable sorting algorithm?

  • No, Shell Sort is not a stable sorting algorithm. This means that the relative order of equal elements might not be preserved after sorting. 
  • Ensure Data Integrity: For applications where preserving the initial order of identical elements is critical, leverage the stability of merge or insertion sort.

Q5. What is the basic idea behind Shell Sort, and how does it differ from insertion sort?

  • Shell Sort is an optimization of insertion sort. Instead of swapping adjacent elements, Shell Sort’s initial step involves comparing elements with larger gaps, gradually decreasing the gap size. 
  • This approach allows for more significant movement of out-of-place elements early on, leading to faster overall sorting.

Q6. How does the choice of gap sequence affect Shell Sort’s performance?

  • The gap sequence determines how the gaps are reduced throughout the sorting process. Different sequences can significantly impact the algorithm’s efficiency. 
  • Popular choices for gap sequences in Shell Sort are the original Shell sequence (which involves dividing by 2), Knuth’s sequence, and Hibbard’s sequence.
  • Finding an optimal gap sequence is an area of ongoing research.

Related Topics:

Scroll to Top