- Selection sorting is also called a simple sorting method. The selection sort is also based on the comparison method.
- In this method, we repeatedly compare the first element to the rest of the elements in the list. If a smaller element is found, it is swapped with the currently selected element.
- After completion of the first iteration, the smallest element in the list will be placed in the first index of an array a[0].
- After these, we select the element at the second position in the list and it is compared with all the remaining elements.
- If any element is smaller than the selected element then both are swapped. This procedure is repeated till the entire list is sorted.
Table of Contents
Algorithm for Selection Sort
- Find the Smallest:
- Begin with the first element in your unsorted list.
- Iterate through the remaining elements, comparing each to the current “smallest” element.
- If a smaller element is encountered, designate it as the new “smallest” element.
- Swap:
- Once you’ve identified the smallest element in the current pass, swap its position with the first unsorted element.
- This effectively places the smallest element in its correct, sorted position at the beginning of the list.
- Repeat:
- Move to the second element in the list.
- Repeat steps 1 and 2, finding the smallest element among the remaining unsorted items and swapping it into the second position.
- Continue:
- Keep iterating through the list, repeating steps 1 and 2 for each remaining position.
- With each pass, the sorted portion of the list grows, and the unsorted portion shrinks.
- Sorted:
- The algorithm concludes when you’ve reached the end of the list.
- At this point, every element has been placed in its correct, sorted order.
Working of Selection Sort
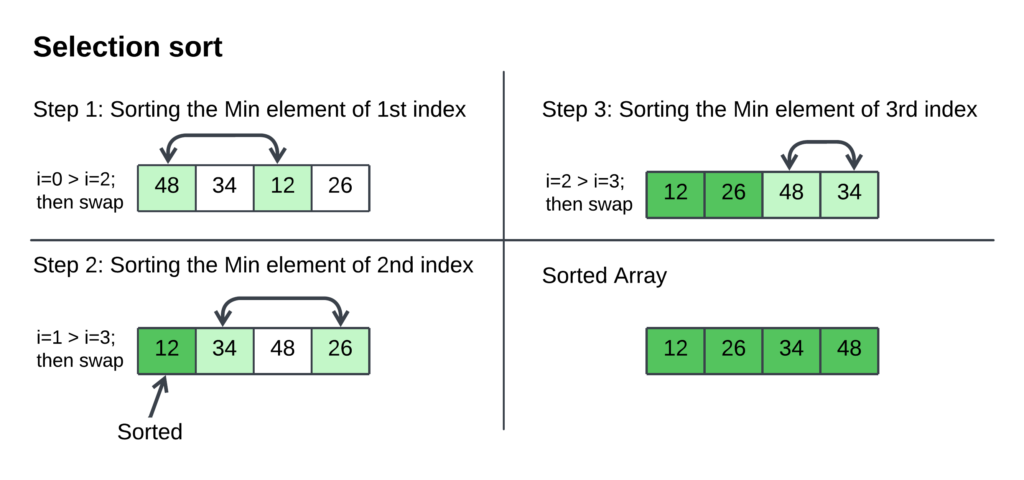
The Selection Sort process on a list of numbers: [48, 34, 12, 26].
- Step 1: Finding the Minimum in the Unsorted Portion
- Index i starts at 0: The algorithm focuses on the first position in the list.
- Scanning for the smallest: It compares 48 with the remaining elements (34, 12, 26) and identifies 12 as the smallest.
- Swap: 48 and 12 are swapped, placing the smallest element (12) at the beginning.
- Result: The list becomes [12, 34, 48, 26]. The first element is now sorted.
- Step 2: Finding the Minimum in the Remaining Unsorted Portion
- Index i is now 1: The algorithm moves to the second position.
- Scanning for the smallest: It compares 34 with the remaining unsorted elements (48, 26) and determines that 26 is the smallest.
- Swap: 34 and 26 are swapped.
- Result: The list becomes [12, 26, 48, 34]. The first two elements are now sorted.
- Step 3: Finding the Minimum in the Remaining Unsorted Portion
- Index i is now 2: The algorithm moves to the third position.
- Scanning for the smallest: Since only two unsorted elements (48, 34) remain, 34 is the smallest.
- Swap: 48 and 34 are swapped.
- Result: The list becomes [12, 26, 34, 48]. The first three elements are now sorted.
- Sorted Array
- Index i would be 3: However, the algorithm stops here as all elements are sorted.
- Final Result: The sorted list is [12, 26, 34, 48].
Selection Sort Program Implementation
def selection_sort(arr):
"""Sorts a list using the Selection Sort algorithm.
Args:
arr: The list to be sorted.
"""
n = len(arr) # Get the length of the list
for i in range(n): # Iterate through each position in the list
# Find the minimum element in the remaining unsorted portion
min_index = i
for j in range(i + 1, n):
if arr[j] < arr[min_index]:
min_index = j
# Swap the found minimum element with the first element
arr[i], arr[min_index] = arr[min_index], arr[i]
# Example usage:
data = [64, 25, 12, 22, 11]
selection_sort(data)
print("Sorted array:", data)
#include <iostream>
#include <vector>
using namespace std;
void selectionSort(vector<int>& arr) {
/* Sorts a vector using the Selection Sort algorithm.
Args:
arr: The vector to be sorted (passed by reference to modify in place).
*/
int n = arr.size(); // Get the size of the vector
for (int i = 0; i < n - 1; i++) {
// Iterate through each position in the vector (except the last)
// Find the index of the minimum element in the unsorted portion
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// Swap the found minimum element with the first element
swap(arr[minIndex], arr[i]);
}
}
int main() {
// Example usage:
vector<int> data = {64, 25, 12, 22, 11};
selectionSort(data);
cout << "Sorted array: ";
for (int num : data) {
cout << num << " ";
}
cout << endl;
return 0;
}
import java.util.Arrays;
public class SelectionSort {
public static void selectionSort(int[] arr) {
/* Sorts an array using the Selection Sort algorithm.
Args:
arr: The array to be sorted.
*/
int n = arr.length; // Get the length of the array
for (int i = 0; i < n - 1; i++) {
// Iterate through each position in the array (except the last)
//Find the index of the minimum element in the unsorted portion
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// Swap the found minimum element with the first element
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
public static void main(String[] args) {
// Example usage:
int[] data = {64, 25, 12, 22, 11};
selectionSort(data);
System.out.println("Sorted array: " + Arrays.toString(data));
}
}
#include <stdio.h>
void selectionSort(int arr[], int n) {
/* Sorts an array using the Selection Sort algorithm.
Args:
arr: The array to be sorted.
n: The length of the array.
*/
for (int i = 0; i < n - 1; i++) {
// Iterate through each position in the array (except the last)
// Find the index of the minimum element in the unsorted portion
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// Swap the found minimum element with the first element
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
int main() {
// Example usage:
int data[] = {64, 25, 12, 22, 11};
int n = sizeof(data) / sizeof(data[0]); // Calculate the length of the array
selectionSort(data, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", data[i]);
}
printf("\n");
return 0;
}
Output:
Sorted array: 11 12 22 25 64 Complexity Analysis of Selection Sort Algorithm
| Complexity | Selection Sort |
| Time Complexity | Best Case/Average Case/Worst Case: O(n^2) |
| Auxiliary Space | O(1) |
| Space Complexity | O(1) |
Advantages of Selection Sort
- Selection sort is very easy to implement.
- It can be used for small data sets.
- It is 60% more efficient than the bubble sort.
Disadvantages of Selection Sort
- Quadratic Time Complexity: Selection Sort’s performance degrades significantly with larger lists due to its O(n²) time complexity, making it unsuitable for handling extensive datasets efficiently.
- Inefficient Swapping: It often performs unnecessary swaps, even when elements are already in their correct positions, leading to suboptimal performance compared to algorithms like insertion sort.
- Not Adaptive: Unlike some sorting algorithms, Selection Sort doesn’t adjust its behavior based on the initial order of the elements, leading to a consistent number of comparisons regardless of the input data’s structure.
How to Optimize Selection Sort
1. Bidirectional Selection Sort (Double Selection Sort):
- Instead of finding only the minimum element in each pass, this variation simultaneously finds both the minimum and maximum elements.
- In each iteration, the minimum is placed at the beginning of the unsorted portion, and the maximum is placed at the end.
- This reduces the total number of comparisons, as you effectively sort two elements per pass.
2. Early Termination:
- If, during a pass, you find that no swaps are necessary (meaning the elements are already in order), you can terminate the algorithm early.
- This is especially beneficial when the input data is partially sorted.
3. Heap Selection Sort:
- This variant replaces the linear search for the minimum element with a min-heap data structure.
- Building the heap initially takes O(n) time, but subsequent minimum extractions are faster (O(log n)).
- This can improve the overall performance of larger datasets.
FAQs Related to Selection Sort
Q1. Is Selection Sort an in-place sorting algorithm?
- Yes, Selection Sort is an in-place algorithm, meaning it doesn’t require additional memory proportional to the input size.
- It directly modifies the original array during the sorting process.
Q2. How does Selection Sort compare to Bubble Sort in terms of performance and efficiency?
- Both Selection Sort and Bubble Sort have a time complexity of O(n²), making them inefficient for large datasets.
- However, Selection Sort generally performs fewer swaps than Bubble Sort, which can be slightly advantageous in scenarios where swapping operations are costly.
Q3. Can you provide a real-world example where Selection Sort might be used?
While not the most efficient for large datasets, Selection Sort might be suitable for scenarios like:
- Sorting a small list of items where performance isn’t critical.
- Educational purposes, as it’s relatively simple to understand and implement.
- Situations where memory usage is a constraint, as it operates in place.
Q4. In what scenarios would you choose Selection Sort over other sorting algorithms?
Selection Sort might be preferred when:
- Dealing with small lists where the O(n²) complexity isn’t a major concern.
- Memory usage is limited, as it operates in place.
- Simplicity and ease of implementation are prioritized over performance.
Q5. Can Selection Sort be optimized? If so, how?
- Yes, there are a few optimization techniques, such as Bidirectional Selection Sort (finding both min and max), early termination (stopping when no swaps are needed), and Heap Selection Sort (using a min-heap).
- However, these offer marginal improvements and don’t change the fundamental O(n²) complexity.
Q6. Is Selection Sort a stable sorting algorithm?
- No, the Selection Sort is not stable. It may change the relative order of elements with equal values during the sorting process.
Related topics:
