What is Radix Sort?
- Radix sort is a linear sorting algorithm. Radix sort is one type of bucket sort.
- In this Radix sort, the elements will be sorted based on distribution.
- When Radix sort is done on the integers, sorting is done on each in the numerical sequence in a number.
- The sorting proceeds from the least significant digit to the most significant digit.
- The number of passes of this sort will depend upon the largest number of an array having a maximum number of digits.
Radix Sort Algorithm
- Sorting takes place by distributing the list of numbers into a bucket by passing through individual digits of a given number one by one beginning with the least significant digit. The number of buckets is ten since we have numbers from zero to nine.
- After each pass, the numbers are collected from the buckets keeping the bucket numbers in sequential order.
- Recursively re-distribute the numbers as in step 1 taking into account, the next most significant digit of the number, and follow step 2.
Table of Contents
Working of Radix Sort with an example
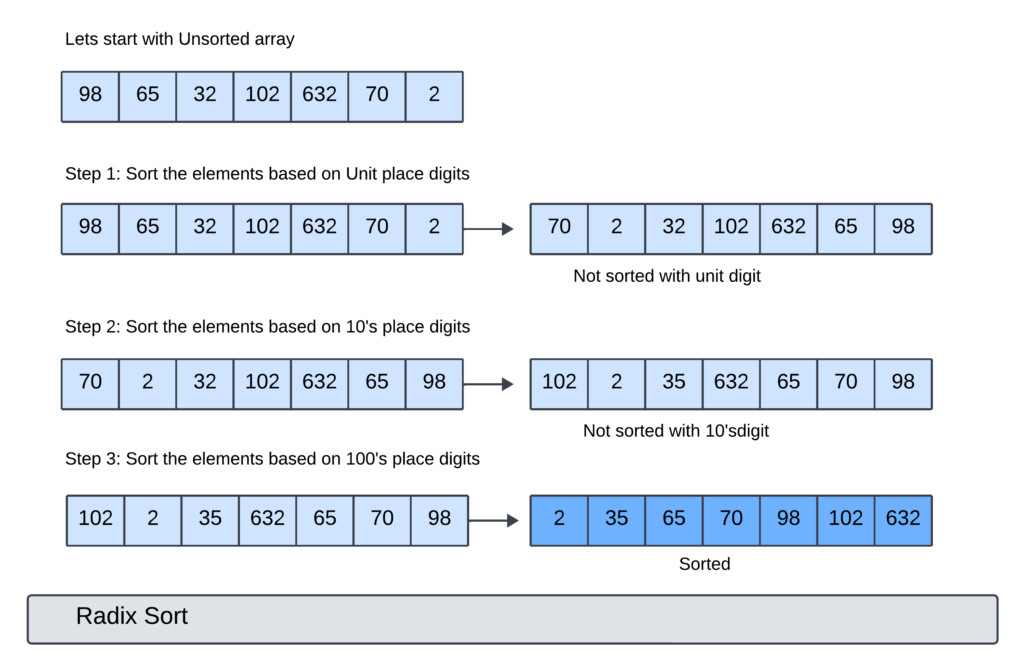
Step 1: Find the largest element in the array.
- In the image, the largest element is 632.
Step 2: Allocate a new array with identical dimensions to the original array.
- This array will be used to store the sorted elements.
Step 3: For each digit in the largest element, starting from the least significant digit, do the following:
- Create a new array that is 10 times the size of the original array.
- For each element in the original array, put it into the new array at the index of its digit. For example, if the entry is 32, put it into the new array at index 2.
- Sort the new array using counting sort.
- Copy the sorted elements back into the original array.
Step 4: Repeat step 3 for each digit in the largest element, starting from the least significant digit.
- In the image, the largest element has three digits, so we need to repeat step 3 three times.
Step 5: The array is now sorted.
- In the image, the sorted array is 2, 32, 65, 70, 98, 102, and 632.
Radix Sort Program Implementation
def counting_sort(arr, exp1):
"""Performs counting sort on the array based on the specified digit place value."""
n = len(arr)
# Initialize the output array and count array
output = [0] * n
count = [0] * 10
# Count the occurrences of each digit
for i in range(n):
index = arr[i] // exp1 # Get the digit at the specified place value
count[index % 10] += 1
# Calculate the cumulative count
for i in range(1, 10):
count[i] += count[i - 1]
# Place the elements in sorted order into the output array
i = n - 1
while i >= 0:
index = arr[i] // exp1
output[count[index % 10] - 1] = arr[i]
count[index % 10] -= 1
i -= 1
# Copy the sorted elements back into the original array
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
"""Main radix sort function."""
# Find the maximum element to determine the number of digits
max1 = max(arr)
# Perform counting sort for every digit
exp = 1
while max1 // exp > 0:
counting_sort(arr, exp)
exp *= 10
# Example usage
data = [170, 45, 75, 90, 802, 24, 2, 66]
radix_sort(data)
print("Sorted array:", data)
#include <iostream>
#include <vector>
#include <algorithm> // for max_element
using namespace std;
void countingSort(vector<int>& arr, int exp) {
// Get size of the input array
int n = arr.size();
// Initialize output array and count array
vector<int> output(n, 0);
vector<int> count(10, 0);
// Count the occurrences of each digit
for (int i = 0; i < n; i++) {
count[(arr[i] / exp) % 10]++;
}
// Calculate cumulative count
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// Place elements in sorted order into the output array
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy sorted elements back to the original array
for (int i = 0; i < n; i++) {
arr[i] = output[i];
}
}
void radixSort(vector<int>& arr) {
// Find the maximum element to know number of digits
int maxVal = *max_element(arr.begin(), arr.end());
// Do counting sort for every digit. Note that instead
// of passing digit number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; maxVal / exp > 0; exp *= 10) {
countingSort(arr, exp);
}
}
int main() {
vector<int> data = {170, 45, 75, 90, 802, 24, 2, 66};
radixSort(data);
cout << "Sorted array: ";
for (int num : data) {
cout << num << " ";
}
cout << endl;
return 0;
}
import java.util.Arrays;
public class RadixSort {
// A utility function to get maximum value in arr[]
static int getMax(int arr[]) {
int mx = arr[0];
for (int i = 1; i < arr.length; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to the digit represented by exp.
static void countSort(int arr[], int exp) {
int n = arr.length;
// The output array elements that will have sorted arr
int output[] = new int[n];
int i;
// Initialize count array as 0
int count[] = new int[10];
Arrays.fill(count,0);
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[ (arr[i]/exp)%10 ]++;
// Change count[i] so that count[i] now contains the actual position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[ (arr[i]/exp)%10 ] - 1] = arr[i];
count[ (arr[i]/exp)%10 ]--;
}
// Copy the output array to arr[], so that arr[] now contains sorted numbers according to current digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of size n using Radix Sort
static void radixsort(int arr[]) {
// Find the maximum number to know number of digits
int m = getMax(arr);
// Do counting sort for every digit. Note that instead
// of passing digit number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; m/exp > 0; exp *= 10)
countSort(arr, exp);
}
// Driver Code
public static void main(String[] args) {
int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
// Function Call
radixsort(arr);
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " ");
}
}
#include <stdio.h>
#include <stdlib.h> // for malloc and free
// A utility function to get maximum value in arr[]
int getMax(int arr[], int n) {
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to the digit represented by exp.
void countSort(int arr[], int n, int exp) {
// The output array elements that will have sorted arr
int* output = (int*)malloc(n * sizeof(int));
// Initialize count array as 0
int count[10] = {0};
// Store count of occurrences in count[]
for (int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains the actual position of this digit in output[]
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now contains sorted numbers according to current digit
for (int i = 0; i < n; i++)
arr[i] = output[i];
free(output); // Release the dynamically allocated memory
}
// The main function to that sorts arr[] of size n using Radix Sort
void radixsort(int arr[], int n) {
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that instead
// of passing digit number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
int main() {
int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
int n = sizeof(arr) / sizeof(arr[0]);
// Function Call
radixsort(arr, n);
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
Output:
Sorted array: [2, 24, 45, 66, 75, 90, 170, 802]Time Complexity of Radix Sort:
- Best Case/Average Case/Worst Case: O(n + k)
Advantages of Radix Sort:
- Radix sort is a basic sorting method.
- With proper implementation, radix sort demonstrates exceptional speed, often outperforming other sorting methods.
Disadvantages of Radix Sort:
- Radix sort is less preferable to other sorting methods.
- Radix sort has a higher space complexity than other sorting methods due to its need for additional arrays to store buckets and element counts.
- Radix sort is dependent on the digits.
Related FAQs
Q1. What is the Radix Sort Algorithm and How Does It Work?
- Radix Sort is a non-comparative sorting algorithm that sorts data with integer keys by grouping keys by the individual digits that share the same significant position and value.
- It sorts by assigning elements into buckets based on each digit, starting from the least significant digit (LSD) and moving towards the most significant digit (MSD).
- Radix Sort leverages the efficiency of Counting Sort as a subroutine for each digit sorting pass.
Q2. Is Radix Sort Stable?
- Yes, Radix Sort is a stable sorting algorithm. If two elements have the same value, their relative order in the sorted output will be the same as in the original input.
Q3. When Should You Use Radix Sort?
- Radix Sort is particularly well-suited for scenarios where: – The input data consists of integers or strings that can be treated as integers.
- The range of values is reasonably small, or the number of digits in the elements is limited. – Stability is a requirement, as Radix Sort preserves the original order of equal elements.
Q4. Is Radix Sort In-Place or Out-of-Place?
- Radix Sort can be implemented both in-place and out-of-place. The most common implementations use additional space for creating buckets and temporary arrays, making them out-of-place.
- While optimized in-place variations of radix sort exist, they often come with increased complexity in both comprehension and implementation.
Q5. How Does Radix Sort Compare to Other Sorting Algorithms?
- Radix Sort, a non-comparative algorithm, differs from comparison-based sorting methods like Quicksort and Merge Sort.
- It excels when dealing with integers or data that can be treated as integers with a limited range.
- For large datasets with a wide range of values, comparison-based algorithms might be more suitable due to their O(n log n) average-case time complexity.
Q6. Can Radix Sort be Used to Sort Floating-Point Numbers?
- Yes, Radix Sort can be adapted to sort floating-point numbers. While efficient, radix sort necessitates preprocessing steps to align decimal points and correctly handle negative numbers.
- One approach involves converting floating-point numbers into fixed-point representations or integers before applying Radix Sort.
Related topics:
