What is Quick Sort?
Quick sort is the widely used sorting algorithm that C. A. R Hoare developed. Quick sort is also called partition exchange sort. This approach is highly effective due to its divide-and-conquer strategy.
In quick sort, we take one element as the pivot element from the list of elements in the array.
The pivot element is also called the key element. Generally, we take the first element of the array as the pivot element. Re-arrange the elements in the array such that all the elements are less than the pivot element that appears on the LHS of the pivot element and the elements present on the RHS are greater than the pivot element.
Now we can partition the array into two sub-arrays as the pivot element is placed in the correct position. This is called a partition operation. Recursively sort the two sub-arrays by using quick sort.
Even though Quick Sort uses a divide-and-conquer strategy there is no need to merge the sub-arrays.
Take the first element as the pivot element.
Scan the pivot element from left to right and find the position of the first greatest element then pivot, say it as i.
Scan the pivot element from right to left and find the position of the first smallest and last element then pivot the Component and say it as j.
If i<j, interchange a[i] with a[j] otherwise interchange pivot with a[i].
The main logic of the quick sort is
{
if(i<j)
interchange a[i] with a[j];
else
interchange pivot element with a[i];
}Table of Contents
Quick Sort Algorithm
The Quick Sort Strategy: Divide, Conquer, and Sort
Quick Sort operates on a simple yet powerful “divide and conquer” principle:
1. Pivot Selection: An element within the array is chosen as the “pivot.”
2. Partitioning: The array is rearranged, placing elements smaller than the pivot to its left and larger elements to its right. This places the pivot in its final sorted position.
3. Recursive Sorting: The partitioning process is successfully implemented through recursion to the sub-arrays on either side of the pivot until the entire array is sorted.
Quick Sort Algorithm Working with an example
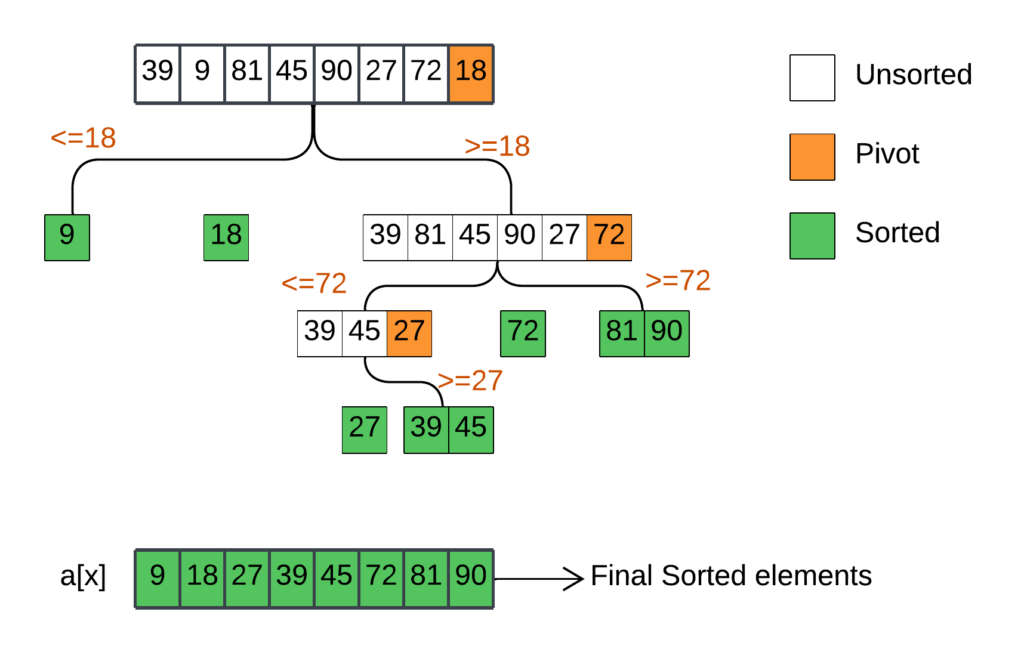
Let’s see Quick Sort in action with a sample array:
[39, 9, 81, 45, 90, 27, 72, 18]
Step 1: Choosing the Pivot
The rightmost element, 18, is selected as the pivot (highlighted in orange). The pivot is the element around which the array will be partitioned.
Step 2: Partitioning
The array is rearranged so that:
- All elements smaller than the pivot (18) are placed to its left.
- All elements greater than or equal to the pivot are placed to its right.
After partitioning, the array looks like this:
[9, 18, 39, 81, 45, 90, 27, 72]
Notice that the pivot (18) is now in its correct sorted position.
Step 3: Recursive Sorting
The algorithm is recursively applied to the sub-arrays formed on either side of the pivot:
- Left Sub-array: [9]
- Since this sub-array has only one element, it’s already sorted.
- Right Sub-array: [39, 81, 45, 90, 27, 72]
- 72 is chosen as the pivot.
- After partitioning: [39, 45, 27, 72, 81, 90]
- Recursive calls are made on [39, 45, 27] and [81, 90]… and so on.
Step 4: Base Case and Combining
The recursive process concludes when each sub-array is reduced to a single element (inherently sorted) or none. At this point, the entire original array is sorted. The final sorted array is shown at the bottom of the image:
[9, 18, 27, 39, 45, 72, 81, 90]
Key Points
- Pivot Choice: The choice of pivot can vary. In this example, the rightmost element is always chosen.
- Efficiency: Quick Sort’s average-case time complexity is O(n log n), making it very efficient for large datasets.
- In-Place Sorting: Quick Sort typically operates directly on the input array, minimising extra memory usage.
Quick Sort Program Implementation
def quick_sort(arr):
"""
Sorts an array in-place using the Quick Sort algorithm.
Args:
arr: The array to be sorted.
"""
if len(arr) < 2: # Base case: arrays of size 0 or 1 are already sorted
return arr
else:
pivot = arr[0] # Choose the first element as the pivot
less = [i for i in arr[1:] if i <= pivot] # Elements smaller than or equal to pivot
greater = [i for i in arr[1:] if i > pivot] # Elements larger than pivot
return quick_sort(less) + [pivot] + quick_sort(greater) # Recursive calls
# Example usage
arr = [39, 9, 81, 45, 90, 27, 72, 18]
sorted_arr = quick_sort(arr)
print(sorted_arr) # Output: [9, 18, 27, 39, 45, 72, 81, 90]
#include <iostream>
#include <vector>
using namespace std;
// Function to partition the array around a pivot
int partition(vector<int>& arr, int low, int high) {
int pivot = arr[high]; // Choose the rightmost element as the pivot
int i = (low - 1); // Index of smaller element
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than or equal topivot
if (arr[j] <= pivot) {
i++; // Increment index of smaller element
swap(arr[i], arr[j]); // Swap elements at i and j
}
}
swap(arr[i + 1], arr[high]); // Place pivot in its correct position
return (i + 1); // Return the new pivot index
}
// Recursive function to implement Quick Sort
void quickSort(vector<int>& arr, int low, int high) {
if (low < high) {
// Partitioning index is returned by partition()
int pi = partition(arr, low, high);
// Recursively sort elements before and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main() {
vector<int> arr = {39, 9, 81, 45, 90, 27, 72, 18};
cout << "Unsorted array: ";
for (int num : arr) {
cout << num << " ";
}
quickSort(arr, 0, arr.size() - 1);
cout << "\nSorted array: ";
for (int num : arr) {
cout << num << " ";
}
return 0;
}
import java.util.Arrays;
public class QuickSort {
public static void quickSort(int[] arr, int low, int high) {
if (low < high) { // Check if subarray has at least two elements
int pivotIndex = partition(arr, low, high); // Partition the array
quickSort(arr, low, pivotIndex - 1); // Recursively sort left subarray
quickSort(arr, pivotIndex + 1, high); // Recursively sort right subarray
}
}
private static int partition(int[] arr, int low, int high) {
int pivot = arr[high]; // Choose the rightmost element as pivot
int i = (low - 1); // Index of smaller element
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) { // If current element is smaller than or equal to pivot
i++;
swap(arr, i, j); // Swap elements at i and j
}
}
swap(arr, i + 1, high); // Place pivot in its correct position
return i + 1; // Return the new pivot index
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arr = {39, 9, 81, 45, 90, 27, 72, 18};
System.out.println("Unsorted array: " + Arrays.toString(arr));
quickSort(arr, 0, arr.length - 1);
System.out.println("Sorted array: " + Arrays.toString(arr));
}
}
#include <stdio.h>
// Function to swap two elements in an array
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// Function to partition the array around a pivot
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // Choose the rightmost element as pivot
int i = (low - 1); // Index of smaller element
for (int j = low; j < high; j++) {
// If current element is smaller than or equal to pivot
if (arr[j] <= pivot) {
i++; // Increment index of smaller element
swap(&arr[i], &arr[j]); // Swap elements at i and j
}
}
swap(&arr[i + 1], &arr[high]); // Place pivot in its correct position
return (i + 1); // Return the new pivot index
}
// Recursive function to implement Quick Sort
void quickSort(int arr[], int low, int high) {
if (low < high) { // Check if subarray has at least two elements
int pi = partition(arr, low, high); // Partition the array
quickSort(arr, low, pi - 1); // Recursively sort left subarray
quickSort(arr, pi + 1, high); // Recursively sort right subarray
}
}
int main() {
int arr[] = {39, 9, 81, 45, 90, 27, 72, 18};
int n = sizeof(arr) / sizeof(arr[0]); // Calculate the number of elements in the array
printf("Unsorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
quickSort(arr, 0, n - 1);
printf("\nSorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
}
Output:
Unsorted array: 39 9 81 45 90 27 72 18
Sorted array: 9 18 27 39 45 72 81 90Quick Sort Complexity Analysis
| Complexity | Best Case | Average Case | Worst Case |
| Time Complexity | O(n log n) | O(n log n) | O(n^2) |
| Auxiliary Space | O(log n) | O(log n) | O(n) |
| Space Complexity | O(log n) | O(log n) | O(n) |
Explanation:
- Time Complexity:
- Best Case: Occurs when the pivot element consistently divides the array into two nearly equal halves. In this case, the partitioning and recursive calls lead to a time complexity of O(n log n).
- Average Case: The average time complexity is also O(n log n), making it highly efficient for most practical scenarios.
- Less Optimal Scenario: Occurs when pivot selection consistently results in unbalanced partitions. This can happen if the array is already sorted or reverse-sorted. The worst-case time complexity degrades to O(n^2), similar to less efficient sorting algorithms like Bubble Sort.
- Auxiliary Space:
- Quick Sort primarily uses recursive function calls for its operations. The space complexity depends on the recursion depth, typically O(log n) in the best and average cases.
- In the worst case, the recursion depth can become O(n), leading to higher space usage.
- Space Complexity:
- Quick Sort is an in-place sorting algorithm, meaning it doesn’t require significant additional memory beyond the input array.
- In most scenarios, the dominant factor in space complexity is the O(log n) auxiliary space utilised for recursion.
When to Choose Quick Sort
Quick Sort is a superb choice when you need to:
- Quickly sort large datasets: It excels in average-case scenarios.
- Optimise for memory usage: Its in-place nature is often advantageous.
- Prioritising efficiency: When the emphasis is on speed and worst-case performance is not a critical constraint, Quick Sort emerges as a strong candidate.
Advantages and Disadvantages of Quick Sort
Advantages
- Efficiency: Quick Sort excels for large datasets with an average time complexity of O(n log n), thanks to its divide-and-conquer approach.
- In-Place Sorting: It sorts data directly in the array, saving memory.
- Cache-Friendly: It works on localised data portions, improving memory access.
- Versatile: It adapts to various data types and can be optimised for specific cases.
- Parallelisable: Its recursive nature allows for parallel sorting on multiple processors.
Disadvantages
- Worst-Case Performance: Can degrade to O(n^2) in rare cases (sorted arrays).
- Unstable Sorting: This doesn’t preserve the order of equal elements.
- Recursion Overhead: Potential for stack overflow with massive datasets.
- Implementation Complexity: Complex to implement efficiently, especially for beginners.
- Not Ideal for Linked Lists: Better choices exist for linked list sorting.
Related FAQs
Absolutely! Here are three more frequently asked questions about Quick Sort, along with SEO-friendly formatting:
Q1. Is Quick Sort a stable sorting algorithm?
- Quick Sort is unstable, meaning the order of equal elements might change after sorting. Use Merge Sort or Insertion Sort for stability.
Q2. How can I optimise Quick Sort for better performance?
- Quick Sort can be optimised with better pivot choices and hybrid approaches for small sub-arrays.
Q3. Are there any real-world applications of Quick Sort?
Yes, Quick Sort finds applications in various fields:
- Database systems: Sorting large datasets for efficient querying and retrieval.
- Operating systems: Sorting files and processes.
- Data analysis: Sorting data for statistical analysis and visualisation.
- Programming languages: Built-in sorting functions often use Quick Sort or hybrid variations.
Q4. Why is Quick Sort considered a fast algorithm?
- Quick Sort’s average time complexity is O(n log n), making it one of the fastest sorting algorithms in most scenarios.
- Its efficiency stems from the divide-and-conquer strategy, Leading to a rapid decrease in the problem size.
Q5. How does pivot selection affect Quick Sort’s performance?
The choice of pivot significantly impacts Quick Sort’s performance. Common strategies include:
- First element: Simple but can lead to worst-case performance in certain scenarios.
- Last element: Similar to choosing the first element.
- Middle element: Often a better choice than the first or last.
- Random element: Good for avoiding worst-case scenarios, but introduces randomness.
Related topics:
- Bubble Sort Algorithm
- Selection Sort Algorithm
- Insertion Sort Algorithm
- Merge Sort Algorithm
- Shell Sort Algorithm
- Radix Sort Algorithm
- Full detailed Quick Sort
