What is Priority Queue?
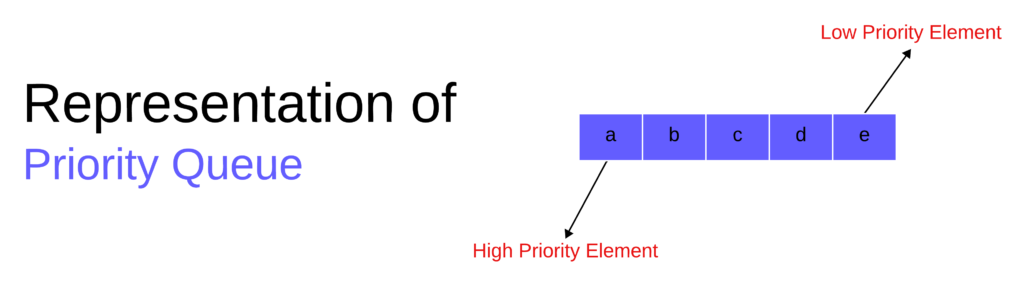
- A priority queue is a set that can contain zero or more elements. Each element is associated with a priority or value.
- Unlike queues, which follow a first-in, first-out (FIFO) order, elements in a priority queue are deleted based on their priority.
- Priority queues remove elements in order of their priority, either increasing or decreasing, rather than the order of arrival.
- There are two types of priority queues:
- 1. Min priority queue
- 2. Max priority queue
- Min priority queue: The collection of elements within the items can be inserted arbitrarily, but only the smallest element can be removed.
- Max priority queue: Collection of elements in which insertion of items can be in any order but only the largest element can be removed.
- In the priority queue, the elements are arranged in any order out of which only the smallest or largest element is allowed to be deleted each time.
- Priority queues can be constructed using either arrays or linked lists.
- The data structure heap is used to implement the priority queue effectively.
Example: Imagine a triage system in a hospital, where patients with more urgent needs are treated first, regardless of their arrival time. Priority queues work similarly – elements with higher priority are dequeued before those with lower priority.
Various operations that can be performed on priority queue are
- Find an element
- Insert a new element
- Remove or delete an element
The following is the abstract data type specification for a max priority queue. The specification for a minimum priority queue is identical to a regular queue, except for the operations related to finding and removing the element with the lowest priority.
Table of Contents
ABSTRACT DATA TYPE(ADT):
Abstract data type max priority queue
{
Instances
A finite set of elements, each with an assigned priority.
empty(): Check if the queue is empty and return the result.
size(): Return the size of the queue.
top(): Retrieve the highest-priority element.
del(): Dequeue the element with the maximum priority.
insert(x): Enqueue the element x.
}
Priority Queue Implement by Using:
- Array
- Linked List
- Heap data structure
- Binary Search Tree
Why Use an Array?
- Arrays provide a simple and direct way to store the elements of our priority queue.
- Arrays, while potentially less performant than binary heaps for large datasets, shine in their simplicity, making them ideal for smaller datasets or scenarios where ease of implementation is key.
Algorithm Steps:
- Initialization:
- Declare an array of a fixed size to represent the priority queue.
- Initialize a variable, size, to 0. This will track the number of elements currently in the queue.
- Enqueue (Insert with Priority):
- Find the Correct Position:
- Starting from the end of the array (size – 1) and moving towards the beginning, compare the priority of the new element with the priority of existing elements.
- Shift existing elements with lower priority one position to the right to make space for the new element.
- Insert the New Element:
- Once the correct position is found, insert the new element into the array.
- Increment size:
- Increase size by 1 to reflect the addition of the new element.
- Find the Correct Position:
- Dequeue (Remove Highest Priority):
- Retrieve the Element at Index 0:
- The element with the highest priority will always be at the beginning of the array (index 0). Retrieve this element.
- Shift Elements:
- Shift all remaining elements one position to the left to fill the gap created by removing the first element.
- Decrement size:
- Decrease size by 1 to reflect the removal of the element.
- Return the Retrieved Element:
- Return the element that was removed from the front of the array.
- Retrieve the Element at Index 0:
- Peek (View Highest Priority):
- Return Element at Index 0:
- Simply return the element at the beginning of the array (index 0), representing the highest priority element.
- Return Element at Index 0:
Program Implementation using Array:
class PriorityQueue:
def __init__(self, max_size):
self.max_size = max_size
self.array = [None] * max_size # Initialize array with None values
self.size = 0 # Current size of the priority queue
def is_empty(self):
# Check if the priority queue is empty
return self.size == 0
def is_full(self):
# Check if the priority queue is full
return self.size == self.max_size
def enqueue(self, item):
if self.is_full():
print("Priority Queue is full. Cannot enqueue.")
return
# Find the correct position to insert the new item
i = self.size - 1
while i >= 0 and item < self.array[i]:
self.array[i + 1] = self.array[i] # Shift elements to the right
i -= 1
# Insert the new item at the correct position
self.array[i + 1] = item
self.size += 1
def dequeue(self):
if self.is_empty():
print("Priority Queue is empty. Cannot dequeue.")
return None
# Retrieve the highest priority element (at index 0)
highest_priority_item = self.array[0]
# Shift elements to the left to remove the dequeued item
for i in range(1, self.size):
self.array[i - 1] = self.array[i]
self.size -= 1
return highest_priority_item
def peek(self):
if self.is_empty():
print("Priority Queue is empty.")
return None
return self.array[0]
def display(self):
if self.is_empty():
print("Priority Queue is empty.")
return
print("Priority Queue elements:", end=" ")
for i in range(self.size):
print(self.array[i], end=" ")
print()
# Example usage:
my_queue = PriorityQueue(5)
my_queue.enqueue(3)
my_queue.enqueue(1)
my_queue.enqueue(4)
my_queue.enqueue(2)
my_queue.display() # Output: 1 2 3 4
print("Dequeued:", my_queue.dequeue()) # Output: 1
my_queue.display() # Output: 2 3 4#include <iostream>
using namespace std;
class PriorityQueue {
private:
int* array; // Array to store priority queue elements
int maxSize;
int size; // Current size of the priority queue
public:
PriorityQueue(int maxSize) {
this->maxSize = maxSize;
array = new int[maxSize];
size = 0; // Initialize size to 0
}
bool isEmpty() {
return size == 0;
}
bool isFull() {
return size == maxSize;
}
void enqueue(int item) {
if (isFull()) {
cout << "Priority Queue is full. Cannot enqueue." << endl;
return;
}
// Find the correct position to insert the new item
int i = size - 1;
while (i >= 0 && item < array[i]) {
array[i + 1] = array[i]; // Shift elements to the right
i--;
}
// Insert the new item at the correct position
array[i + 1] = item;
size++;
}
int dequeue() {
if (isEmpty()) {
cout << "Priority Queue is empty. Cannot dequeue." << endl;
return -1; // Indicate queue underflow
}
// Retrieve the highest priority element (at index 0)
int highestPriorityItem = array[0];
// Shift elements to the left to fill the gap
for (int i = 1; i < size; i++) {
array[i - 1] = array[i];
}
size--;
return highestPriorityItem;
}
int peek() {
if (isEmpty()) {
cout << "Priority Queue is empty." << endl;
return -1; // Indicate queue underflow
}
return array[0];
}
void display() {
if (isEmpty()) {
cout << "Priority Queue is empty." << endl;
return;
}
cout << "Priority Queue elements: ";
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
}
};
int main() {
PriorityQueue pq(5);
pq.enqueue(3);
pq.enqueue(1);
pq.enqueue(4);
pq.enqueue(2);
pq.display(); // Output: 1 2 3 4
cout << "Dequeued: " << pq.dequeue() << endl; // Output: 1
pq.display(); // Output: 2 3 4
return 0;
}class PriorityQueue {
private int[] array; // Array to store priority queue elements
private int maxSize;
private int size; // Current size of the priority queue
public PriorityQueue(int maxSize) {
this.maxSize = maxSize;
array = new int[maxSize];
size = 0; // Initialize size to 0
}
public boolean isEmpty() {
return size == 0;
}
public boolean isFull() {
return size == maxSize;
}
public void enqueue(int item) {
if (isFull()) {
System.out.println("Priority Queue is full. Cannot enqueue.");
return;
}
// Find the correct position to insert the new item
int i = size - 1;
while (i >= 0 && item < array[i]) {
array[i + 1] = array[i]; // Shift elements to the right
i--;
}
// Insert the new item at the correct position
array[i + 1] = item;
size++;
}
public int dequeue() {
if (isEmpty()) {
System.out.println("Priority Queue is empty. Cannot dequeue.");
return -1; // Indicate queue underflow
}
// Retrieve the highest priority element (at index 0)
int highestPriorityItem = array[0];
// Shift elements to the left to fill the gap
for (int i = 1; i < size; i++) {
array[i - 1] = array[i];
}
size--;
return highestPriorityItem;
}
public int peek() {
if (isEmpty()) {
System.out.println("Priority Queue is empty.");
return -1; // Indicate queue underflow
}
return array[0];
}
public void display() {
if (isEmpty()) {
System.out.println("Priority Queue is empty.");
return;
}
System.out.print("Priority Queue elements: ");
for (int i = 0; i < size; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
PriorityQueue pq = new PriorityQueue(5);
pq.enqueue(3);
pq.enqueue(1);
pq.enqueue(4);
pq.enqueue(2);
pq.display(); // Output: 1 2 3 4
System.out.println("Dequeued: " + pq.dequeue()); // Output: 1
pq.display(); // Output: 2 3 4
}
}#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100 // Define a maximum size for the queue
// Structure to represent the priority queue
typedef struct {
int* array; // Array to store queue elements
int maxSize;
int size; // Current size of the queue
} PriorityQueue;
// Function to initialize the priority queue
PriorityQueue* createPriorityQueue(int maxSize) {
PriorityQueue* pq = (PriorityQueue*)malloc(sizeof(PriorityQueue));
pq->maxSize = maxSize;
pq->array = (int*)malloc(maxSize * sizeof(int));
pq->size = 0; // Initialize size to 0
return pq;
}
// Function to check if the queue is empty
int isEmpty(PriorityQueue* pq) {
return pq->size == 0;
}
// Function to check if the queue is full
int isFull(PriorityQueue* pq) {
return pq->size == pq->maxSize;
}
// Function to enqueue (insert) an element into the priority queue
void enqueue(PriorityQueue* pq, int item) {
if (isFull(pq)) {
printf("Priority Queue is full. Cannot enqueue.\n");
return;
}
// Find the correct position to insert the new item
int i = pq->size - 1;
while (i >= 0 && item < pq->array[i]) {
pq->array[i + 1] = pq->array[i]; // Shift elements to the right
i--;
}
// Insert the new item at the correct position
pq->array[i + 1] = item;
pq->size++;
}
// Function to dequeue (remove and return) the highest priority element
int dequeue(PriorityQueue* pq) {
if (isEmpty(pq)) {
printf("Priority Queue is empty. Cannot dequeue.\n");
return -1; // Indicate queue underflow
}
// The highest priority element is always at index 0
int highestPriorityItem = pq->array[0];
// Shift elements to the left to fill the gap
for (int i = 1; i < pq->size; i++) {
pq->array[i - 1] = pq->array[i];
}
pq->size--;
return highestPriorityItem;
}
// Function to peek (return) the highest priority element without removing it
int peek(PriorityQueue* pq) {
if (isEmpty(pq)) {
printf("Priority Queue is empty.\n");
return -1; // Indicate queue underflow
}
return pq->array[0];
}
// Function to display the elements of the priority queue
void display(PriorityQueue* pq) {
if (isEmpty(pq)) {
printf("Priority Queue is empty.\n");
return;
}
printf("Priority Queue elements: ");
for (int i = 0; i < pq->size; i++) {
printf("%d ", pq->array[i]);
}
printf("\n");
}
int main() {
PriorityQueue* pq = createPriorityQueue(5);
enqueue(pq, 3);
enqueue(pq, 1);
enqueue(pq, 4);
enqueue(pq, 2);
display(pq); // Output: 1 2 3 4
printf("Dequeued: %d\n", dequeue(pq)); // Output: Dequeued: 1
display(pq); // Output: 2 3 4
free(pq->array);
free(pq);
return 0;
}Output:
Priority Queue elements: 1 2 3 4
Dequeued: 1
Priority Queue elements: 2 3 4Complexity Analysis of Priority Queue Implementations
| Operation | Array | Linked List | Binary Heap | Binary Search Tree |
| Insertion | O(n) | O(n) | O(log n) | O(log n) |
| Deletion | O(n) | O(1) | O(log n) | O(log n) |
| Peek | O(1) | O(1) | O(1) | O(log n) |
| Space Used | O(n) | O(n) | O(n) | O(n) |
Benefits of Array-Based Priority Queues:
- Simplicity: Easier to understand and implement compared with more complex structures like binary heaps.
- Suitable for Small Datasets: Can be efficient for managing smaller datasets where the overhead of a heap might be unnecessary.
Applications:
- Operating systems use priority queues to schedule jobs, with real-time jobs taking precedence over foreground and background jobs.
- Priority queues are employed in network communication to allocate bandwidth efficiently.
- Priority queues are used in simulation modeling to handle discrete events efficiently.
Related FAQs:
1. Priority Queue vs. Heap: What’s the Difference?
- A priority queue is an abstract data type (a concept), while a heap (often a binary heap) is a concrete data structure used to implement a priority queue. Think of it like this: a priority queue is the blueprint, and a heap is the building.
2. When Should I Use a Priority Queue?
- Use a priority queue whenever you need to efficiently retrieve and process elements based on their importance or urgency, rather than their order of arrival.
3. How Do I Choose the Right Priority Queue Implementation?
- The best implementation depends on your application’s needs.
- Binary heaps are the go-to choice for efficient priority queue implementations in most situations, while arrays are suitable for smaller datasets or less demanding scenarios.
- Consider factors like insertion/deletion frequency and the need for sorted output.
4. Can Priority Queues Have Duplicate Priorities?
- Yes, priority queues can handle elements with the same priority. The order in which elements with the same priority are dequeued depends on the specific implementation and might vary.
5. Are There Libraries for Priority Queues in Popular Programming Languages?
- Absolutely! Programming languages provide built-in libraries or data structures that implement priority queues. For example, Python has the heapq module, Java has the PriorityQueue class, and C++ has the priority_queue container adapter. Using these libraries can save you time and effort in implementation.
