What is Merge Sort?
Merge Sort is a sorting algorithm that employs a divide-and-conquer strategy. Divide means partitioning that array of n elements into two sub-arrays containing n/2 elements.
If an array contains one element then it is a sorted array. If a sub-array has more than one element, split it into two halves, each containing approximately half the original number of elements.
Conquer means sorting the two sub-arrays recursively using merge-sort. After that merge the two sorted sub-arrays of size n/2 to produce the sorted array of n elements. The merge sort uses two functions such as merge sort and merge.
The algorithm logic of merge sort is
If(low<high)
{
mid=(low+high)/2;
msort(low, mid);
msort(mid+1, high);
msort(low, mid, high);
}Table of Contents
Merge Sort Algorithm
Merge Sort follows a “divide and conquer” strategy:
- Divide: The input array is repeatedly divided into halves until each subarray contains only one element (considered sorted by default).
- Conquer: Each pair of sorted subarrays is merged to create larger, sorted subarrays.
- Combine: This merging process continues until the entire array is combined into a single, sorted unit.
Merge Sort Working with an example
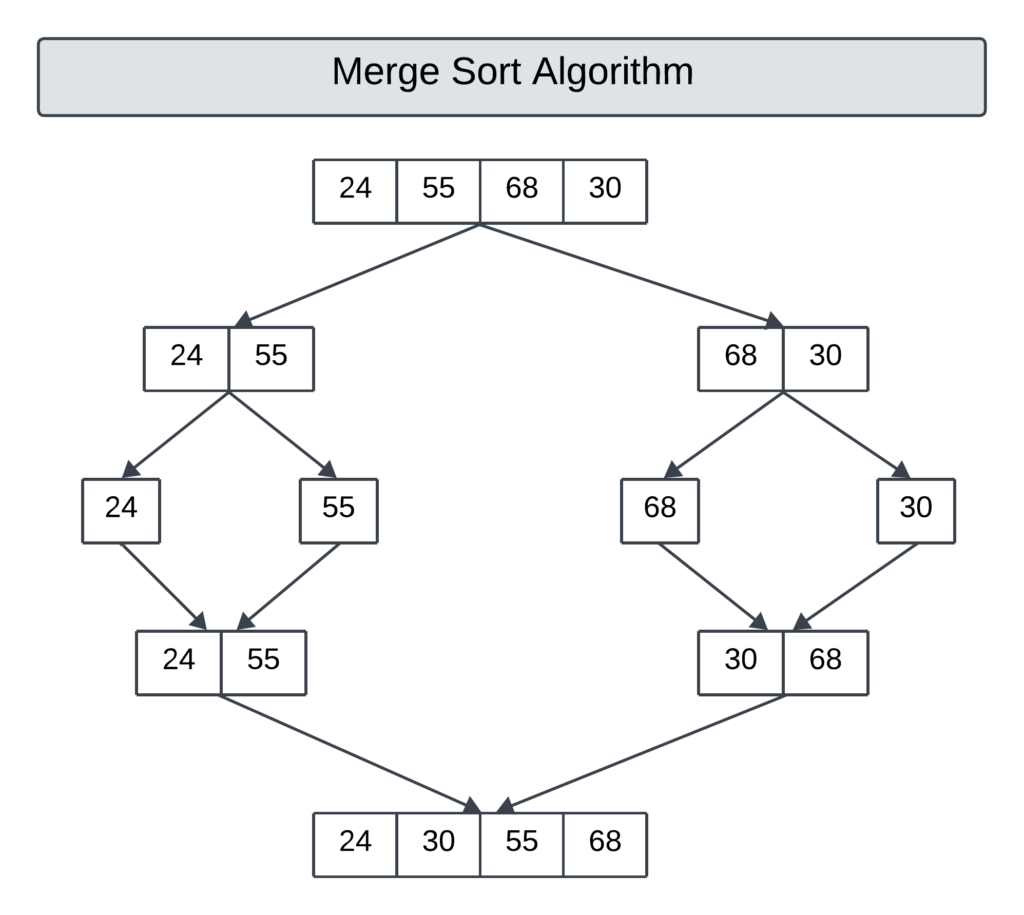
Consider the array: [24, 55, 68, 30]
- Divide:
- The initial unsorted array [24, 55, 68, 30] is divided into two halves: [24, 55] and [68, 30].
- Each half is further divided into [24] [55] and [68] [30].
- Conquer (Base Case):
- At this level, each subarray contains a single element, and a single element is considered inherently sorted.
- Combine (Merge):
- The sorted subarrays [24] and [55] are merged, resulting in [24, 55].
- The sorted subarrays [30] and [68] are merged, resulting in [30, 68].
- Combine (Merge):
- The sorted subarrays [24, 55] and [30, 68] are merged. During this merge, elements are compared and placed in the correct order in the combined array, resulting in the final sorted array: [24, 30, 55, 68].
Merge Sort Program Implementation
def merge_sort(arr):
"""Sorts an array using the Merge Sort algorithm."""
if len(arr) > 1:
# 1. Divide: Find the middle point and divide into subarrays
mid = len(arr) // 2 # Floor division to get integer index
left_half = arr[:mid]
right_half = arr[mid:]
# 2. Conquer: Recursively sort both halves
merge_sort(left_half)
merge_sort(right_half)
# 3. Combine: Merge the sorted halves back into arr
i = j = k = 0 # Indices for left, right, and merged arrays
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
arr[k] = left_half[i]
i += 1
else:
arr[k] = right_half[j]
j += 1
k += 1
# If elements remain in either left or right half, copy them to the merged array
while i < len(left_half):
arr[k] = left_half[i]
i += 1
k += 1
while j < len(right_half):
arr[k] = right_half[j]
j += 1
k += 1
# Example usage
data = [8, 3, 1, 7, 0, 10, 2]
merge_sort(data)
print("Sorted array:", data)
#include <iostream>
#include <vector>
using namespace std;
void merge(vector<int>& arr, int left, int mid, int right) {
/* Merges two sorted subarrays into one */
int n1 = mid - left + 1; // Size of left subarray
int n2 = right - mid; // Size of right subarray
// Create temporary arrays
vector<int> L(n1), R(n2);
// Copy data to temporary arrays
for (int i = 0; i < n1; i++) L[i] = arr[left + i];
for (int j = 0; j < n2; j++) R[j] = arr[mid + 1 + j];
// Merge the temporary arrays back into arr[left..right]
int i = 0, j = 0, k = left; // Indices for left, right, and merged arrays
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of L[], if any
while (i < n1) {
arr[k] = L[i];
i++; k++;
}
// Copy the remaining elements of R[], if any
while (j < n2) {
arr[k] = R[j];
j++; k++;
}
}
void mergeSort(vector<int>& arr, int left, int right) {
/* Recursive function to sort an array using Merge Sort */
if (left < right) {
// 1. Divide: Find the middle point and divide into subarrays
int mid = left + (right - left) / 2;
// 2. Conquer: Recursively sort both halves
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 3. Combine: Merge the sorted halves back into arr
merge(arr, left, mid, right);
}
}
int main() {
vector<int> data = {8, 3, 1, 7, 0, 10, 2};
mergeSort(data, 0, data.size() - 1);
cout << "Sorted array: ";
for (int num : data) cout << num << " ";
cout << endl;
return 0;
}
import java.util.Arrays;
public class MergeSort {
public static void mergeSort(int[] arr, int left, int right) {
/* Recursive function to sort an array using Merge Sort */
if (left < right) {
// 1. Divide: Find the middle point and divide into subarrays
int mid = left + (right - left) / 2; // Avoids potential overflow
// 2. Conquer: Recursively sort both halves
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 3. Combine: Merge the sorted halves back into arr
merge(arr, left, mid, right);
}
}
private static void merge(int[] arr, int left, int mid, int right) {
/* Merges two sorted subarrays into one */
int n1 = mid - left + 1; // Size of left subarray
int n2 = right - mid; // Size of right subarray
// Create temporary arrays
int[] L = new int[n1];
int[] R = new int[n2];
// Copy data to temporary arrays
for (int i = 0; i < n1; ++i) L[i] = arr[left + i];
for (int j = 0; j < n2; ++j) R[j] = arr[mid + 1 + j];
// Merge the temporary arrays back into arr[left..right]
int i = 0, j = 0;
int k = left; // Index for the merged array
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of L[], if any
while (i < n1) {
arr[k] = L[i];
i++; k++;
}
// Copy the remaining elements of R[], if any
while (j < n2) {
arr[k] = R[j];
j++; k++;
}
}
public static void main(String[] args) {
int[] data = {8, 3, 1, 7, 0, 10, 2};
mergeSort(data, 0, data.length - 1);
System.out.println("Sorted array: " + Arrays.toString(data));
}
}
#include <stdio.h>
#include <stdlib.h>
void merge(int arr[], int left, int mid, int right) {
/* Merges two sorted subarrays into one */
int n1 = mid - left + 1; // Size of left subarray
int n2 = right - mid; // Size of right subarray
// Create temporary arrays
int L[n1], R[n2];
// Copy data to temporary arrays
for (int i = 0; i < n1; i++) L[i] = arr[left + i];
for (int j = 0; j < n2; j++) R[j] = arr[mid + 1 + j];
// Merge the temporary arrays back into arr[left..right]
int i = 0, j = 0, k = left; // Indices for left, right, and merged arrays
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of L[], if any
while (i < n1) {
arr[k] = L[i];
i++; k++;
}
// Copy the remaining elements of R[], if any
while (j < n2) {
arr[k] = R[j];
j++; k++;
}
}
void mergeSort(int arr[], int left, int right) {
/* Recursive function to sort an array using Merge Sort */
if (left < right) {
// 1. Divide: Find the middle point and divide into subarrays
int mid = left + (right - left) / 2;
// 2. Conquer: Recursively sort both halves
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 3. Combine: Merge the sorted halves back into arr
merge(arr, left, mid, right);
}
}
int main() {
int data[] = {8, 3, 1, 7, 0, 10, 2};
int size = sizeof(data) / sizeof(data[0]);
mergeSort(data, 0, size - 1);
printf("Sorted array: ");
for (int i = 0; i < size; i++) {
printf("%d ", data[i]);
}
printf("\n");
return 0;
}
Output:
Sorted array: [0, 1, 2, 3, 7, 8, 10]Complexity Analysis
| Complexity | Best Case | Average Case | Worst Case |
| Time Complexity | O(n log n) | O(n log n) | O(n log n) |
| Auxiliary Space Complexity | O(n) | O(n) | O(n) |
| Space Complexity | O(n) | O(n) | O(n) |
Advantages and Disadvantages of Merge Sort in DSA:
Advantages
- Consistent Time Complexity: Merge Sort guarantees a time complexity of O(n log n) in all cases (best, average, and worst). This makes it highly predictable and efficient, especially for large datasets.
- Stable Sorting: Merge Sort maintains the relative order of equal elements. This is crucial in scenarios where the original order of equal items matters.
- Well-Suited for Linked Lists: Merge Sort is ideal for sorting linked lists because it only requires sequential access to elements, unlike algorithms requiring random access.
- Parallelism: Merge Sort’s divide-and-conquer nature makes it easily parallelisable, allowing you to leverage multiple processors or threads for faster sorting.
- External Sorting: When dealing with datasets too large to fit in memory, Merge Sort can be adapted for external sorting, efficiently handling data stored on disks.
Disadvantages
- Space Complexity: Merge Sort has a space complexity of O(n) due to the need for temporary arrays during the merging process. This can be a concern for memory-constrained environments.
- Recursion Overhead: The recursive implementation of Merge Sort can incur some overhead, although this is usually negligible compared to the overall efficiency.
- Slower for Small Datasets: For the smallest datasets, simpler algorithms like Insertion Sort or Selection Sort might outperform Merge Sort due to its overhead.
- Not In-Place: Merge Sort requires additional memory for the temporary arrays, making it not an in-place sorting algorithm.
- Implementation Complexity: While conceptually elegant, the implementation of Merge Sort can be slightly more complex than other sorting algorithms.
FAQs related to Merge Sort
Q1. Is Merge Sort an in-place sorting algorithm?
- While efficient, Merge Sort does not operate in place, requiring auxiliary memory for the temporary arrays used during the merging step.
Q2. When would you choose Merge Sort over other sorting algorithms?
- Consider Merge Sort for scenarios where maintaining the relative order of equal elements is important, handling substantial datasets, working with linked list structures, or possessing sufficient memory to accommodate its space usage.
- It’s particularly well-suited for scenarios where stability is crucial, such as sorting records based on multiple criteria.
Q3. Can Merge Sort be parallelised?
- Yes, Merge Sort is easily parallelisable due to its divide-and-conquer nature. Each half of the array can be sorted independently in parallel, and then the sorted halves can be merged.
- This can lead to significant speedups on multi-core systems.
Q4. Why is Merge Sort considered a stable sorting algorithm?
- Merge Sort maintains the relative order of equal elements. Two elements have the same value, their order in the sorted output will be the same as in the original input.
Q5. Can you explain the ‘divide and conquer’ strategy used in Merge Sort?
- The Merge Sort algorithm recursively splits the input array into progressively smaller subarrays, continuing until each subarray is reduced to a single element, which is trivially sorted.
- It then merges these sorted subarrays to form a larger sorted array.
Q6. What are the main advantages and disadvantages of Merge Sort compared to other sorting algorithms like QuickSort or HeapSort?
- Merge Sort’s main advantages are its consistent time complexity, stability, and suitability for linked lists.
- Drawbacks include the need for additional memory to store temporary arrays and a marginally higher overhead compared to certain other sorting methods.
Q7. How would you implement Merge Sort for linked lists?
- Merge Sort is well-suited for linked lists because it only requires sequential access. You can implement it by recursively dividing the list into halves, sorting each half, and then merging the sorted halves back together.
Related Topics:
