Linked List in Data Structure

What is a Linked List?

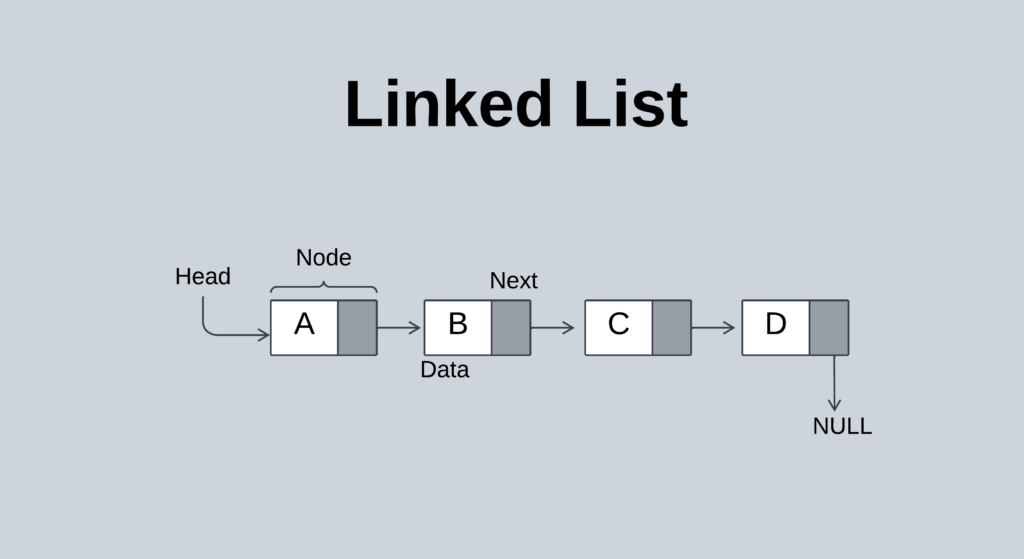
In computer science, a linked list is a linear collection of data elements called nodes.
Each node of the linked list consists of data and links. Data can hold various types of information, including integers, characters, and more.
The link of the node contains the address of the next node.
The link is a pointer which points to the next node.
The last node of the linked list will have no connection with the other node. So fill the link field of the final node with a NULL value.
In C language the node can be represented using self-referential structure. Linked lists are simple and most commonly used data structure.
They can be used to implement other data structures such as stacks, queues, etc…

Ex:

data

link

Node

Array	Linked List
An array is a collection of similar data items stored under a common name.	A linked list is a sequential collection of elements connected by pointers.
In an array, elements can be accessed randomly.	Linked lists require sequential access to their elements.
In an array, elements are stored in consecutive memory locations.	Linked lists offer flexibility in memory allocation, as elements can be placed in any available space, with the address of the following value stored in the current node.
Inserting or deleting elements in arrays can be slower compared to other data structures due to the consecutive storage of elements	Linked lists offer efficient insertion and deletion operations because we only need to modify pointers.
In arrays, memory is allocated at compiler time.	In linked lists, memory is allocated at run time.
Arrays can be 1-D, 2-D, multi-dimensional arrays.	Linked lists may be singly linked lists, doubly-linked lists, and circular linked lists.
In arrays each element is independent.	In the linked list each element is dependent.
Unlike linked lists, arrays don’t require pointers, eliminating the need for extra memory to store them.	In the linked list adjacency between the elements is maintained with the help of pointers. So we require extra space to store the pointer.

The two most important applications of linked lists are polynomial representation and sparse matrix.

Polynomials consist of various terms, each containing a coefficient and an exponent. A polynomial P(x) is in the form of

P(x) = Axⁿ+Bx^n-1++Cx^n-2+….+yx+z

Where A, B, C,……., Z are real numbers and n is a non-negative integer called the degree of the polynomial.

Ex: 6x³+9x²+7x+4

Each term in a polynomial is represented as a node.

A node consists of a coefficient, an exponent, and a link.

Dynamic Sizing: Linked lists adjust their size dynamically, eliminating the risk of overflow errors common to fixed arrays.
Efficient Insertions/Deletions: Adding or removing elements in linked lists is efficient, especially at the beginning or middle, as it doesn’t require shifting elements like arrays.
Memory Efficiency: Linked lists allocate memory only as needed, optimizing memory usage compared to arrays, which might allocate more space than required.
Building Block for Advanced Structures: Linked lists are foundational for building more complex data structures like stacks, queues, trees, and graphs, extending their utility.
Representing Data Relationships: Linked lists effectively model relationships between data elements in simple sequences or complex networks, providing a clear representation.