What is Linear Search?
- Linear search is also called sequential search. Linear search is a very simple method for searching an element in a given list of elements.
- Linear search works by comparing the search element with each and every element of the list in a sequential manner until the match is found.
- If the search element is found, then we terminate the search process. If the search element is present in the given list of elements then it is called a successful search otherwise it is called an unsuccessful search.
Table of Contents
Algorithm of Linear Search
Imagine you’re looking for a particular book on a shelf. You start at one end and examine each book in order until you find the one you want or reach the end of the shelf. The linear search algorithm operates in much the same way:
- Start at the Beginning: Begin with the first element in the list.
- Compare: Check if the current element matches the target value.
- Match Found: If yes, you’ve successfully located the target – return its position (index) in the list.
- No Match: If no, move on to the next element.
- Repeat: Continue steps 2 and 3 until you find the target or reach the end of the list. If you reach the end without finding the target, it’s not present in the list.
Working of Linear Search Algorithm
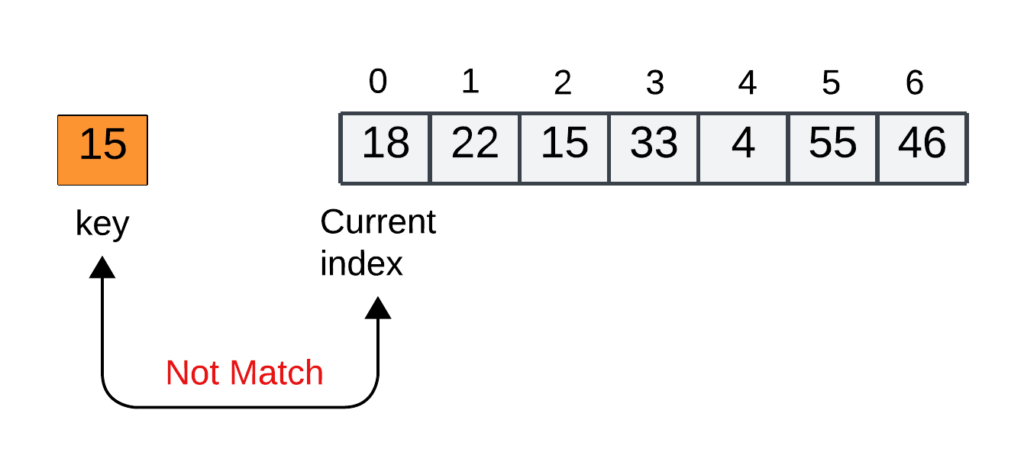
For Example: Let’s Consider the array arr[] = {18, 22, 15, 33, 4, 55, 46} and key = 15.
Step 1: let’s start from the first element of index 0 and compare the key with the current element in the array (arr[i]).
- Comparing the key with the 1st element of index 0 (arr[0]). Not match, So the iterator moves to the next index as a potential match.
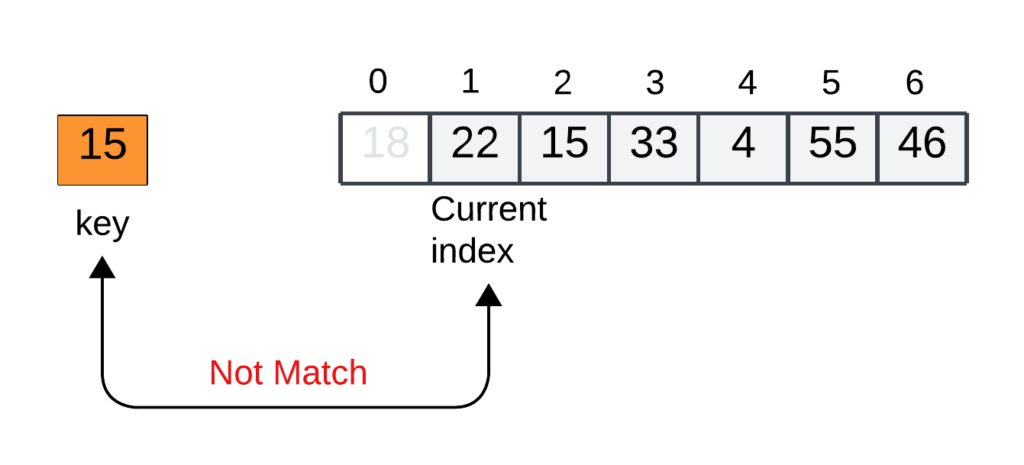
Step 2: Comparing the key with the 2nd element of index 1 (arr[1]), since not match move to the next index of an array.
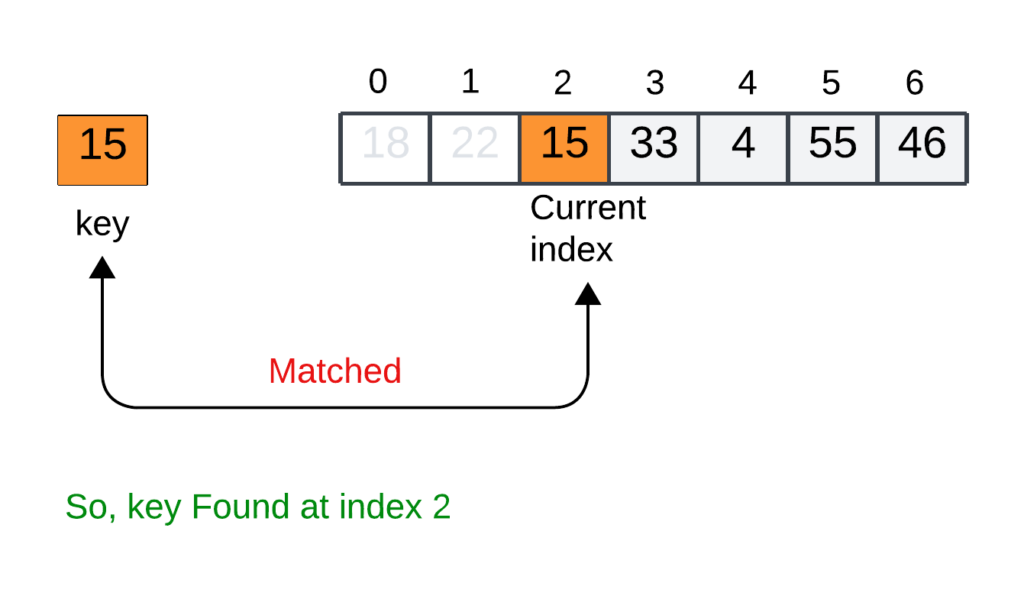
Step 3: Comparing the key with the 3rd element of index 2 (arr[3]), since the value is matched. So, return the index of the element (i.e key is found at 2)
Implementation of Linear Search Algorithm
def linear_search(arr, target):
"""
Searches for a target value within a list using linear search.
Args:
arr: The list to search within.
target: The value to search for.
Returns:
The index of the target if found, otherwise -1.
"""
# Iterate through each element in the list
for i in range(len(arr)):
# Check if the current element matches the target
if arr[i] == target:
return i # Target found, return its index
# Target not found after searching the entire list
return -1
# Example Usage:
my_list = [4, 1, 8, 3, 9, 5]
target_value = 8
result = linear_search(my_list, target_value)
if result != -1:
print("Target found at index:", result)
else:
print("Target not found in the list.")
#include <iostream>
#include <vector>
using namespace std;
int linear_search(const vector<int>& arr, int target) {
/*
Searches for a target value within a vector using linear search.
Args:
arr: The vector to search within.
target: The value to search for.
Returns:
The index of the target if found, otherwise -1.
*/
// Iterate through each element in the vector
for (int i = 0; i < arr.size(); ++i) {
// Check if the current element matches the target
if (arr[i] == target) {
return i; // Target found, return its index
}
}
// Target not found after searching the entire vector
return -1;
}
int main() {
vector<int> my_list = {4, 1, 8, 3, 9, 5};
int target_value = 8;
int result = linear_search(my_list, target_value);
if (result != -1) {
cout << "Target found at index: " << result << endl;
} else {
cout << "Target not found in the list." << endl;
}
return 0;
}
import java.util.ArrayList;
import java.util.List;
public class LinearSearch {
public static int linearSearch(List<Integer> arr, int target) {
/*
Searches for a target value within a list using linear search.
Args:
arr: The list to search within.
target: The value to search for.
Returns:
The index of the target if found, otherwise -1.
*/
// Iterate through each element in the list
for (int i = 0; i < arr.size(); i++) {
// Check if the current element matches the target
if (arr.get(i) == target) {
return i; // Target found, return its index
}
}
// Target not found after searching the entire list
return -1;
}
public static void main(String[] args) {
List<Integer> myList = new ArrayList<>();
myList.add(4);
myList.add(1);
myList.add(8);
myList.add(3);
myList.add(9);
myList.add(5);
int targetValue = 8;
int result = linearSearch(myList, targetValue);
if (result != -1) {
System.out.println("Target found at index: " + result);
} else {
System.out.println("Target not found in the list.");
}
}
}
#include <stdio.h>
#include <stdbool.h>
int linear_search(int arr[], int size, int target) {
/*
Searches for a target value within an array using linear search.
Args:
arr: The array to search within.
size: The number of elements in the array.
target: The value to search for.
Returns:
The index of the target if found, otherwise -1.
*/
// Iterate through each element in the array
for (int i = 0; i < size; i++) {
// Check if the current element matches the target
if (arr[i] == target) {
return i; // Target found, return its index
}
}
// Target not found after searching the entire array
return -1;
}
int main() {
int my_array[] = {4, 1, 8, 3, 9, 5};
int size = sizeof(my_array) / sizeof(my_array[0]); // Calculate the array's size
int target_value = 8;
int result = linear_search(my_array, size, target_value);
if (result != -1) {
printf("Target found at index: %d\n", result);
} else {
printf("Target not found in the array.\n");
}
return 0;
}
Output:
Target found at index: 2Linear Search Algorithm Time and Space Complexity
| Case | Time Complexity | Space Complexity |
| Best Case | O(1) | O(1) |
| Average Case | O(n) | O(1) |
| Worst Case | O(n) | O(1) |
Explanation:
- Time Complexity:
- Best Case: The target element is found at the beginning of the list. We compare only once, and the algorithm finishes.
- Average Case: On average, we need to check about half the elements in the list before finding the target (or determining it’s not present).
- Worst Case: The target element is at the end of the list, or it’s not in the list at all. We need to compare every element.
- Space Complexity:
- Linear search only requires a few variables to keep track of the current index and the target value. It doesn’t use any extra space that grows with the input size.
Key Points:
- O(n) linear time: The time taken grows linearly with the number of elements in the list.
- O(1) constant space: The space used remains constant regardless of the input size.
Advantages of Linear Search
Simplicity: Easy to understand and implement, making it a great starting point for learning search algorithms.
Unsorted Data: Works effectively on lists that aren’t necessarily sorted.
Versatility: Can be applied to various data types (numbers, text, etc.).
Disadvantages of Linear Search
Inefficiency: For large datasets, linear search can be slow because it might need to check every single element.
Not Optimal: Other search algorithms (like binary search) are significantly faster when data is sorted.
When to Use Linear Search
Small Lists: When your list is short, the difference in speed compared to other algorithms is negligible.
Unsorted Data: If your data is unsorted, linear search is a viable option.
Simplicity is Key: If you need a quick and easy-to-understand search solution.
Applications Of Linear Search Algorithm
Finding Contacts:
Phonebooks: Imagine flipping through a physical phonebook to find a specific person’s number. You’re essentially performing a linear search.
Contact Lists: Smartphone apps often use linear search to quickly find contacts based on name or number.
Spell Checkers: Spell checkers compare each word in a document against a dictionary of correctly spelled words. Linear search is a common method to find potential misspellings.
Data Processing:
Simple Databases: When dealing with small databases or unsorted data, linear search is a straightforward way to locate specific records.
Inventory Systems: Linear search can be used to check the availability of products in an inventory list.
Technical Applications:
File Systems: Operating systems may use linear search to locate specific files within a directory.
Security Systems: Intrusion detection systems might use linear search to scan logs for suspicious patterns.
Data Analysis: In certain data analysis tasks, linear search can be used to find specific values or outliers in small datasets.
FAQs on Linear Search Algorithm
Q1: What is the linear search algorithm?
- The linear search algorithm, also known as a sequential search, is a basic search technique used to find a specific value (the “target”) within a list or array.
- It starts at the beginning of the list and checks each element in order until it finds the target or reaches the end.
Q2: How does linear search work?
- Imagine you’re searching for a particular song in a playlist. You’d start from the first song and listen to each one until you find the one you’re looking for or reach the end.
- Linear search works in the same way, comparing each element in a list to the target value.
Q3: When should I use the linear search?
Linear search is suitable in the following situations:
- Small Lists: When the list to search is small, the speed difference compared to other algorithms is negligible.
- Unsorted Data: If the data is not sorted, linear search is a viable option.
- Simplicity is Key: When you need a quick and easy-to-understand search solution.
Q4: How can I implement linear search in different programming languages?
Linear search is straightforward to implement. Here’s a basic example in Python:
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1 # Target not foundQ5: What is the time complexity of linear search?
- The time complexity of linear search is O(n), where ‘n’ is the number of elements in the list.
- This means that in the worst-case scenario (where the target is at the end or not present in the list), the algorithm might have to check all ‘n’ elements.
Q6: Can linear search be used on other data structures besides arrays or lists?
- Yes, linear search can be applied to any linear data structure where you can access elements sequentially, such as linked lists.
- The principle remains the same: iterate through each element until you find the target or reach the end.
Q7: Is linear search suitable for real-time applications?
- While linear search is simple, its O(n) time complexity makes it less efficient for large datasets.
- In real-time applications where speed is critical and the data is large, other algorithms like binary search (for sorted data) or hash tables might be more appropriate choices.
- However, linear search can still be useful in real-time scenarios with small datasets or when simplicity and ease of implementation are priorities.
Related topics:
