What is Insertion Sort?
Insertion sort is a straightforward sorting technique. The main idea behind insertion sort is that it inserts each element into its proper place at the end of the list.
The insertion sort works by moving the current data element past the already sorted values and repeatedly interchanging with the preceding value until it is placed in the correct position.
Insertion Sort Algorithm
1. The first element is sorted: The algorithm begins by assuming the first element is already in its correct position (since it’s the only element considered).
2. Pick the next element: The next unsorted element is selected as the “key.”
3. Compare and shift: The key is compared to the elements in the sorted subarray. If the key is smaller than an element, that element is moved one position to the right to make space for the key.
4. Insert: The key is inserted into its correct position within the sorted subarray.
5. Repeat: Steps 2-4 are repeated for each remaining unsorted element.
Working of Insertion Sort Algorithm with an example
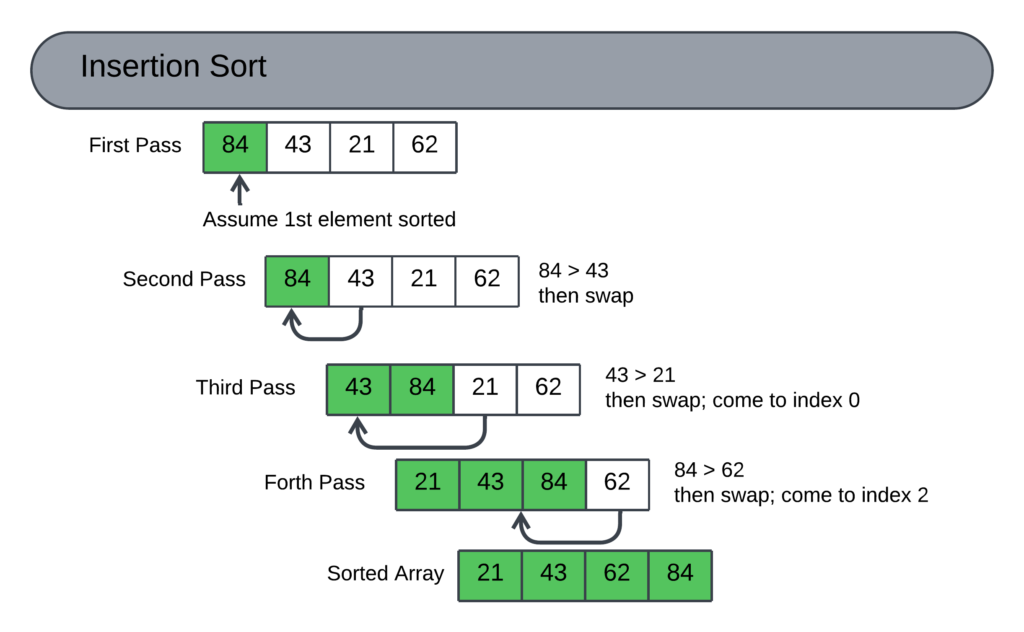
Let’s Consider the list of elements {84, 43, 21, 62}
- Assume the First Element is Sorted:
- The algorithm starts with the first element (84 in this case) and considers it already sorted since it’s the only element looked at.
- Pick the Next Element (Key):
- During the second step, the algorithm selects the second element (43) and labels it as the “key.”
- This is the element we’ll insert into the correct position.
- Compare and Swap:
- The key (43) is compared to the element in the sorted portion (84).
- Since 43 is smaller than 84, they are swapped.
- Third Pass:
- Now, the sorted portion is [43, 84].
- The third element (21) becomes the new key.
- We compare 21 with 84 and then 43, swapping each time as 21 is smaller.
- This continues until 21 reaches the beginning of the array, becoming the new first element.
- Fourth Pass:
- The sorted portion is now [21, 43, 84].
- The fourth element (62) becomes the key.
- Comparisons and swaps occur until 62 finds its correct position between 43 and 84.
- Repeat:
- This process continues for each remaining element in the unsorted portion of the array.
- Each key is compared to the elements in the sorted portion and swapped until it’s in its correct position.
Insertion Sort Program Implementation
def insertion_sort(arr):
"""
This function sorts an array in ascending order using the Insertion Sort algorithm.
Args:
arr: The array to be sorted.
"""
# Iterate through each element in the array starting from the second element (index 1).
for i in range(1, len(arr)):
key = arr[i] # The current element being considered for insertion into the sorted part.
j = i - 1 # Initialize a pointer to the last element in the sorted part.
# While there are elements left in the sorted part and the current element is smaller,
# shift the larger elements one position to the right to make space for the current element.
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
# Insert the current element (key) at its correct position in the sorted part.
arr[j + 1] = key
# Example usage:
if __name__ == "__main__":
arr = [12, 11, 13, 5, 6]
print("Original array:", arr)
insertion_sort(arr)
print("Sorted array:", arr)
#include <iostream>
#include <vector>
using namespace std;
void insertionSort(vector<int>& arr) {
/*
This function sorts an array in ascending order using the Insertion Sort algorithm.
Args:
arr: The vector to be sorted.
*/
// Iterate through each element in the vector starting from the second element (index 1).
for (int i = 1; i < arr.size(); i++) {
int key = arr[i]; // The current element being considered for insertion into the sorted part.
int j = i - 1; // Initialize a pointer to the last element in the sorted part.
/*
While there are elements left in the sorted part and the current element is smaller,
shift the larger elements one position to the right to make space for the current element.
*/
while (j >= 0 && key < arr[j]) {
arr[j + 1] = arr[j];
j--;
}
// Insert the current element (key) at its correct position in the sorted part.
arr[j + 1] = key;
}
}
int main() {
vector<int> arr = {12, 11, 13, 5, 6};
cout << "Original array: ";
for (int num : arr) {
cout << num << " ";
}
insertionSort(arr);
cout << "\nSorted array: ";
for (int num : arr) {
cout << num << " ";
}
return 0;
}
import java.util.Arrays;
public class InsertionSort {
public static void insertionSort(int[] arr) {
/*
This function sorts an array in ascending order using the Insertion Sort algorithm.
Args:
arr: The array to be sorted.
*/
// Iterate through each element in the array starting from the second element (index 1).
for (int i = 1; i < arr.length; i++) {
int key = arr[i]; // The current element being considered for insertion into the sorted part.
int j = i - 1; // Initialize a pointer to the last element in the sorted part.
/*
While there are elements left in the sorted part and the current element is smaller,
shift the larger elements one position to the right to make space for the current element.
*/
while (j >= 0 && key < arr[j]) {
arr[j + 1] = arr[j];
j--;
}
// Insert the current element (key) at its correct position in the sorted part.
arr[j + 1] = key;
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6};
System.out.println("Original array: " + Arrays.toString(arr));
insertionSort(arr);
System.out.println("Sorted array: " + Arrays.toString(arr));
}
}
#include <stdio.h>
void insertionSort(int arr[], int size) {
/*
This function sorts an array in ascending order using the Insertion Sort algorithm.
Args:
arr: The array to be sorted.
size: The size (number of elements) of the array.
*/
// Iterate through each element in the array starting from the second element (index 1).
for (int i = 1; i < size; i++) {
int key = arr[i]; // The current element being considered for insertion into the sorted part.
int j = i - 1; // Initialize a pointer to the last element in the sorted part.
/*
While there are elements left in the sorted part and the current element is smaller,
shift the larger elements one position to the right to make space for the current element.
*/
while (j >= 0 && key < arr[j]) {
arr[j + 1] = arr[j];
j--;
}
// Insert the current element (key) at its correct position in the sorted part.
arr[j + 1] = key;
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6};
int size = sizeof(arr) / sizeof(arr[0]); // Calculate the array size
printf("Original array: ");
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
insertionSort(arr, size);
printf("\nSorted array: ");
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
return 0;
}
Output:
Original array: [12, 11, 13, 5, 6]
Sorted array: [5, 6, 11, 12, 13]Complexity Analysis(Time, Auxiliary, Space) of Insertion Sort in DSA
| Complexity | Explanation |
| Time Complexity | |
| Best Case | O(n) When the input array is already sorted. |
| Worst Case | O(n^2) When the array is in reverse order. |
| Average Case | O(n^2) |
| Auxiliary Space Complexity | O(1) Uses a constant amount of extra space for temporary variables. |
| Space Complexity | O(1) Since auxiliary space complexity is O(1). |
Advantages Insertion Sort Algorithm
- Insertion Sort is simple to code and highly efficient for sorting smaller datasets.
- Insertion sort is efficiently implemented on the data sets which are already in sorted order.
- Insertion sort is twice as fast as bubble sort and almost 40% faster than the selection sort.
- Requires less memory space.
- Insertion sort is an online sorting algorithm that sorts the list whenever a new element is entered.
Disadvantages Insertion Sort Algorithm
- Insertion sort‘s quadratic time complexity (O(n^2)) in average and worst-case scenarios makes it less suitable for handling large or unsorted datasets.
- Inefficient for Randomly Ordered Data: Insertion sort’s efficiency decreases when data is randomly ordered, resulting in slower sorting times.
- Not Suitable for Large Datasets: Insertion sort is impractical for large datasets due to its quadratic time complexity; more efficient algorithms like merge sort or quicksort are preferred.
- Limited Optimization Potential: Insertion sort’s quadratic nature limits performance improvement, despite optimisations like binary search.
- Outperformed by Other Algorithms: Insertion sort is less efficient than merge sort or quicksort for general-purpose sorting.
Insertion Sort related FAQs
Q1. Is Insertion Sort a stable sorting algorithm? What does that mean?
- Yes, Insertion Sort is a stable sorting algorithm. Two elements have the same value, their relative order in the original array will be preserved in the sorted array.
- This can be important when sorting data with multiple attributes, where the stability ensures that equal elements are not reordered arbitrarily.
Q2. Can you provide a real-world example where Insertion Sort might be used?
- Absolutely! Imagine you have a small list of tasks you need to prioritise. You might instinctively use Insertion Sort by taking each task and mentally inserting it into the correct spot in your priority list.
- This is how Insertion Sort could be used in a practical, everyday scenario. It’s also useful when data is frequently added to a mostly sorted list, as it allows for the efficient insertion of new elements.
Q3. How can I improve the performance of Insertion Sort?
While the standard Insertion Sort has its limitations, there are optimisations you can explore:
- Binary Insertion Sort: Instead of linearly searching for the correct position of the key, use binary search. This reduces the number of comparisons, improving the average-case performance, but the worst-case remains O(n^2).
- Hybrid Approaches: Combine Insertion Sort with other algorithms. For example, use Insertion Sort for small subarrays within Merge Sort or QuickSort. This leverages the efficiency of Insertion Sort on smaller datasets while benefiting from the faster average-case performance of the other algorithms for larger datasets.
Q4. How does Insertion Sort compare to other sorting algorithms?
- Insertion Sort excels for small data or when simplicity matters, but consider other algorithms for larger sorts. Algorithms like Merge Sort and QuickSort have better average-case time complexities (O(n log n)) and often outperform Insertion Sort in real-world scenarios with larger inputs.
- However, Insertion Sort remains a valuable tool for specific use cases where its strengths align with your needs.
Q5. When should I use Insertion Sort?
- Insertion Sort shines when:
- Your dataset is small.
- Your dataset is mostly sorted already.
- You prioritise simplicity and don’t need the fastest possible sort for large data.
Related topics:
- Bubble Sort Algorithm
- Selection Sort Algorithm
- Quick Sort Algorithm
- Merge Sort Algorithm
- Shell Sort Algorithm
- Radix Sort Algorithm
