- The binary search algorithm is a high-speed searching method over a list of elements that are in sorted order.
- This algorithm requires a division operation in each iteration, costing computation time.
- David Ferguson proposed a solution for addressing this problem.
- He proposed a decision tree similar to the Fibonacci tree and followed the searching method by using this tree.
- The construction of the Fibonacci tree is to understand the method in the Fibonacci search.
- The nth term of the Fibonacci number is given by
f(n)=f(n-1)+f(n-2) for n≥2
where f0=0 and f1=1.
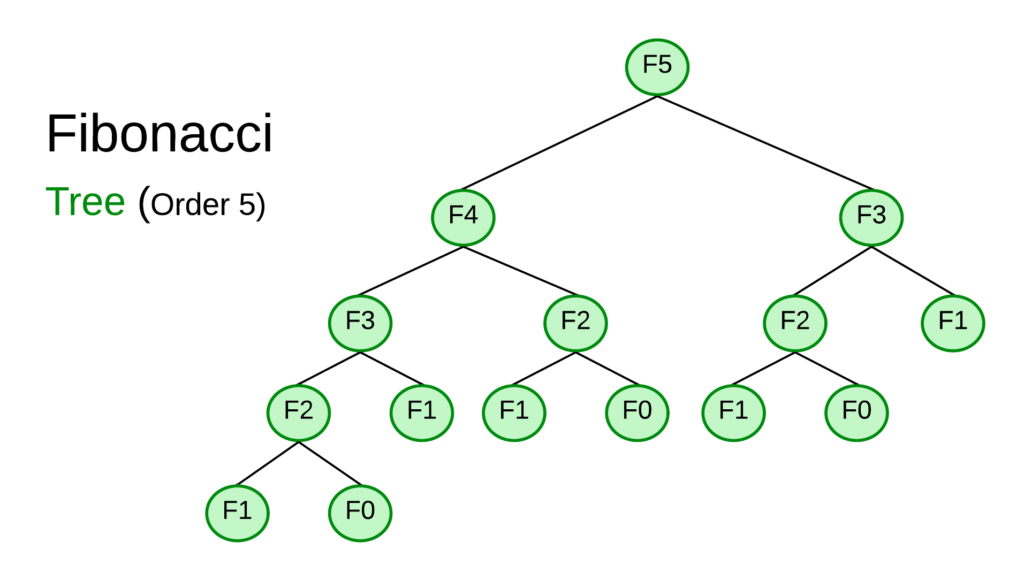
- We expand the nth Fibonacci number in the form of a recurrence tree. We can term this as the Fibonacci tree of order n.
Table of Contents
The next step is to convert the Fibonacci tree to the Fibonacci search tree, we have to follow two rules.
Rule-1:
For all the leaf nodes (do not have any children) corresponding to f1 and f0 we denote them as external nodes redraw them in square boxes and set the values to zero.
The value of each node is replaced by its corresponding Fibonacci number.
Rule-2:
For all nodes corresponding to fi(i≥2) each of them is a Fibonacci search tree of order i such that,
- The root node is fi
- The left sub-tree is f(i-1)
- The right sub-tree is fi-2+fi
The following important observations are noticed in any Fibonacci search tree of order.
- Number of internal nodes=fn+1
- If an internal node contains two internal nodes then the difference of values between a parent and any child is the same and the difference should be a Fibonacci value.
- If an internal node contains one internal node and one external node then the left child value is reduced by 1 to its parent value and the right child value retains the parent value.
- If an internal node contains two external nodes then the left child value is reduced by 1 to its parent value and the right child value retains its parent value.
All leaf nodes will have sequential values from left to right.
Consider the following elements
Search element 40.
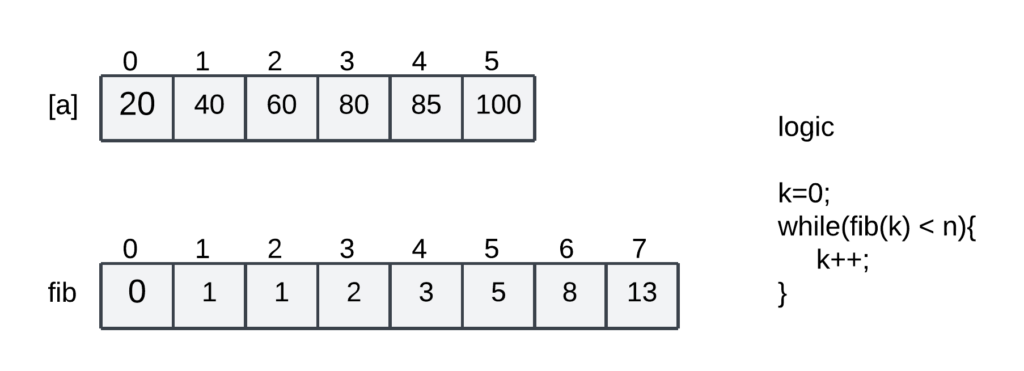
In our example K=6, which is the maximum Fibonacci number to search the element in an array.
So we have to construct an F(K-1) Fibonacci search tree, i.e., an F5 search tree.
Fibonacci tree (order 5)
Fibonacci search tree of order 5.
Implementation of Iterative Fibonacci Search
def fibonacci_search(arr, x, n):
"""
This function performs Fibonacci Search to find the index of 'x' in the sorted array 'arr' of size 'n'.
It returns the index if 'x' is found, else it returns -1.
Args:
arr: Sorted array to search in.
x: Element to be searched.
n: Size of the array.
Returns:
Index of 'x' if found, otherwise -1.
"""
# Initialize Fibonacci numbers
fibM_minus_2 = 0 # (m-2)'th Fibonacci number
fibM_minus_1 = 1 # (m-1)'th Fibonacci number
fibM = fibM_minus_1 + fibM_minus_2 # m'th Fibonacci number
# Find the smallest Fibonacci number greater than or equal to n
while fibM < n:
fibM_minus_2 = fibM_minus_1
fibM_minus_1 = fibM
fibM = fibM_minus_1 + fibM_minus_2
# Marks the eliminated range from front
offset = -1
# While there are elements to be inspected
while fibM > 1:
# Check if fibM_minus_2 is a valid location
i = min(offset + fibM_minus_2, n - 1)
# If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if arr[i] < x:
fibM = fibM_minus_1
fibM_minus_1 = fibM_minus_2
fibM_minus_2 = fibM - fibM_minus_1
offset = i
# If x is less than the value at index fibM_minus_2, cut the subarray after i+1
elif arr[i] > x:
fibM = fibM_minus_2
fibM_minus_1 = fibM_minus_1 - fibM_minus_2
fibM_minus_2 = fibM - fibM_minus_1
# Element found. Return index
else:
return i
# Comparing the last element with x
if fibM_minus_1 and arr[offset + 1] == x:
return offset + 1
# Element not found. Return -1
return -1
# Example usage
arr = [2, 3, 4, 10, 16, 22, 28, 35, 42, 50]
x = 22
n = len(arr)
result = fibonacci_search(arr, x, n)
if result != -1:
print("Found at index:", result)
else:
print("Not found")
#include <iostream>
#include <vector>
using namespace std;
int fibonacciSearch(const vector<int>& arr, int x) {
/*
This function performs Fibonacci Search to find the index of 'x' in the sorted array 'arr'.
Args:
arr: Sorted array to search in.
x: Element to be searched.
Returns:
Index of 'x' if found, otherwise -1.
*/
int n = arr.size();
int fibM_minus_2 = 0; // (m-2)'th Fibonacci number
int fibM_minus_1 = 1; // (m-1)'th Fibonacci number
int fibM = fibM_minus_1 + fibM_minus_2; // m'th Fibonacci number
// Find the smallest Fibonacci number greater than or equal to n
while (fibM < n) {
fibM_minus_2 = fibM_minus_1;
fibM_minus_1 = fibM;
fibM = fibM_minus_1 + fibM_minus_2;
}
int offset = -1; // Marks the eliminated range from front
// While there are elements to be inspected
while (fibM > 1) {
// Check if fibM_minus_2 is a valid location
int i = min(offset + fibM_minus_2, n - 1);
// If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if (arr[i] < x) {
fibM = fibM_minus_1;
fibM_minus_1 = fibM_minus_2;
fibM_minus_2 = fibM - fibM_minus_1;
offset = i;
}
// If x is less than the value at index fibM_minus_2, cut the subarray after i+1
else if (arr[i] > x) {
fibM = fibM_minus_2;
fibM_minus_1 = fibM_minus_1 - fibM_minus_2;
fibM_minus_2 = fibM - fibM_minus_1;
}
// Element found. Return index
else {
return i;
}
}
// Comparing the last element with x
if (fibM_minus_1 && arr[offset + 1] == x) {
return offset + 1;
}
// Element not found. Return -1
return -1;
}
int main() {
vector<int> arr = {2, 3, 4, 10, 16, 22, 28, 35, 42, 50};
int x = 22;
int result = fibonacciSearch(arr, x);
if (result != -1) {
cout << "Found at index: " << result << endl;
} else {
cout << "Not found" << endl;
}
return 0;
}
import java.util.List;
public class FibonacciSearch {
public static int fibonacciSearch(List<Integer> arr, int x) {
/*
This function performs Fibonacci Search to find the index of 'x' in the sorted array 'arr'.
Args:
arr: Sorted list to search in.
x: Element to be searched.
Returns:
Index of 'x' if found, otherwise -1.
*/
int n = arr.size();
int fibM_minus_2 = 0; // (m-2)'th Fibonacci number
int fibM_minus_1 = 1; // (m-1)'th Fibonacci number
int fibM = fibM_minus_1 + fibM_minus_2; // m'th Fibonacci number
// Find the smallest Fibonacci number greater than or equal to n
while (fibM < n) {
fibM_minus_2 = fibM_minus_1;
fibM_minus_1 = fibM;
fibM = fibM_minus_1 + fibM_minus_2;
}
int offset = -1; // Marks the eliminated range from front
// While there are elements to be inspected
while (fibM > 1) {
// Check if fibM_minus_2 is a valid location
int i = Math.min(offset + fibM_minus_2, n - 1);
// If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if (arr.get(i) < x) {
fibM = fibM_minus_1;
fibM_minus_1 = fibM_minus_2;
fibM_minus_2 = fibM - fibM_minus_1;
offset = i;
}
// If x is less than the value at index fibM_minus_2, cut the subarray after i+1
else if (arr.get(i) > x) {
fibM = fibM_minus_2;
fibM_minus_1 = fibM_minus_1 - fibM_minus_2;
fibM_minus_2 = fibM - fibM_minus_1;
}
// Element found. Return index
else {
return i;
}
}
// Comparing the last element with x
if (fibM_minus_1 != 0 && arr.get(offset + 1) == x) {
return offset + 1;
}
// Element not found. Return -1
return -1;
}
public static void main(String[] args) {
List<Integer> arr = List.of(2, 3, 4, 10, 16, 22, 28, 35, 42, 50);
int x = 22;
int result = fibonacciSearch(arr, x);
if (result != -1) {
System.out.println("Found at index: " + result);
} else {
System.out.println("Not found");
}
}
}
#include <stdio.h>
int fibonacciSearch(int arr[], int x, int n) {
/*
This function performs Fibonacci Search to find the index of 'x' in the sorted array 'arr' of size 'n'.
It returns the index if 'x' is found, else it returns -1.
Args:
arr: Sorted array to search in.
x: Element to be searched.
n: Size of the array.
Returns:
Index of 'x' if found, otherwise -1.
*/
int fibM_minus_2 = 0; // (m-2)'th Fibonacci number
int fibM_minus_1 = 1; // (m-1)'th Fibonacci number
int fibM = fibM_minus_1 + fibM_minus_2; // m'th Fibonacci number
// Find the smallest Fibonacci number greater than or equal to n
while (fibM < n) {
fibM_minus_2 = fibM_minus_1;
fibM_minus_1 = fibM;
fibM = fibM_minus_1 + fibM_minus_2;
}
int offset = -1; // Marks the eliminated range from front
// While there are elements to be inspected
while (fibM > 1) {
// Check if fibM_minus_2 is a valid location
int i = (offset + fibM_minus_2 < n - 1) ? offset + fibM_minus_2 : n - 1;
// If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if (arr[i] < x) {
fibM = fibM_minus_1;
fibM_minus_1 = fibM_minus_2;
fibM_minus_2 = fibM - fibM_minus_1;
offset = i;
}
// If x is less than the value at index fibM_minus_2, cut the subarray after i+1
else if (arr[i] > x) {
fibM = fibM_minus_2;
fibM_minus_1 = fibM_minus_1 - fibM_minus_2;
fibM_minus_2 = fibM - fibM_minus_1;
}
// Element found. Return index
else {
return i;
}
}
// Comparing the last element with x
if (fibM_minus_1 && arr[offset + 1] == x) {
return offset + 1;
}
// Element not found. Return -1
return -1;
}
int main() {
int arr[] = {2, 3, 4, 10, 16, 22, 28, 35, 42, 50};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 22;
int result = fibonacciSearch(arr, x, n);
if (result != -1) {
printf("Found at index: %d\n", result);
} else {
printf("Not found\n");
}
return 0;
}
Output:
Found at index: 5Implementation of Recursive Fibonacci Search
def fibonacci_search(arr, x, n, fibM, fibM_minus_1, fibM_minus_2, offset):
"""
Recursive function to perform Fibonacci Search to find the index of 'x' in the sorted array 'arr' of size 'n'.
Args:
arr: Sorted array to search in.
x: Element to be searched.
n: Size of the array.
fibM: Current Fibonacci number (m'th).
fibM_minus_1: (m-1)'th Fibonacci number.
fibM_minus_2: (m-2)'th Fibonacci number.
offset: Eliminated range from the front of the array.
Returns:
Index of 'x' if found, otherwise -1.
"""
# Base case: If fibM becomes 0, element is not present
if fibM == 0:
return -1
# Check if fibM_minus_2 is a valid location
i = min(offset + fibM_minus_2, n - 1)
# If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if arr[i] < x:
return fibonacci_search(arr, x, n, fibM_minus_1, fibM_minus_2, fibM - fibM_minus_1, i)
# If x is less than the value at index fibM_minus_2, cut the subarray after i+1
elif arr[i] > x:
return fibonacci_search(arr, x, n, fibM_minus_2, fibM - fibM_minus_1, fibM_minus_1 - fibM_minus_2, offset)
# Element found. Return index
else:
return i
# Main function to initiate the Fibonacci Search
def main_fibonacci_search(arr, x):
"""
This function initiates the recursive Fibonacci Search by calculating initial Fibonacci numbers.
Args:
arr: Sorted array to search in.
x: Element to be searched.
Returns:
Index of 'x' if found, otherwise -1.
"""
n = len(arr) # Size of the array
fibM_minus_2 = 0 # (m-2)'th Fibonacci number
fibM_minus_1 = 1 # (m-1)'th Fibonacci number
fibM = fibM_minus_1 + fibM_minus_2 # m'th Fibonacci number
# Find the smallest Fibonacci number greater than or equal to n
while fibM < n:
fibM_minus_2 = fibM_minus_1
fibM_minus_1 = fibM
fibM = fibM_minus_1 + fibM_minus_2
return fibonacci_search(arr, x, n, fibM, fibM_minus_1, fibM_minus_2, -1) # Start the search with offset -1
# Example usage
arr = [2, 3, 4, 10, 16, 22, 28, 35, 42, 50]
x = 22
result = main_fibonacci_search(arr, x)
if result != -1:
print("Found at index:", result)
else:
print("Not found")
#include <iostream>
#include <vector>
using namespace std;
int fibonacciSearch(const vector<int>& arr, int x, int n, int fibM, int fibM_minus_1, int fibM_minus_2, int offset) {
/*
Recursive function to perform Fibonacci Search to find the index of 'x' in the sorted array 'arr' of size 'n'.
Args:
arr: Sorted array to search in.
x: Element to be searched.
n: Size of the array.
fibM: Current Fibonacci number (m'th).
fibM_minus_1: (m-1)'th Fibonacci number.
fibM_minus_2: (m-2)'th Fibonacci number.
offset: Eliminated range from the front of the array.
Returns:
Index of 'x' if found, otherwise -1.
*/
// Base case: If fibM becomes 0, element is not present
if (fibM == 0) {
return -1;
}
// Check if fibM_minus_2 is a valid location
int i = min(offset + fibM_minus_2, n - 1);
// If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if (arr[i] < x) {
return fibonacciSearch(arr, x, n, fibM_minus_1, fibM_minus_2, fibM - fibM_minus_1, i);
}
// If x is less than the value at index fibM_minus_2, cut the subarray after i+1
else if (arr[i] > x) {
return fibonacciSearch(arr, x, n, fibM_minus_2, fibM - fibM_minus_1, fibM_minus_1 - fibM_minus_2, offset);
}
// Element found. Return index
else {
return i;
}
}
// Main function to initiate the Fibonacci Search
int mainFibonacciSearch(const vector<int>& arr, int x) {
/*
This function initiates the recursive Fibonacci Search by calculating initial Fibonacci numbers.
Args:
arr: Sorted array to search in.
x: Element to be searched.
Returns:
Index of 'x' if found, otherwise -1.
*/
int n = arr.size();
int fibM_minus_2 = 0;
int fibM_minus_1 = 1;
int fibM = fibM_minus_1 + fibM_minus_2;
// Find the smallest Fibonacci number greater than or equal to n
while (fibM < n) {
fibM_minus_2 = fibM_minus_1;
fibM_minus_1 = fibM;
fibM = fibM_minus_1 + fibM_minus_2;
}
return fibonacciSearch(arr, x, n, fibM, fibM_minus_1, fibM_minus_2, -1);
}
int main() {
vector<int> arr = {2, 3, 4, 10, 16, 22, 28, 35, 42, 50};
int x = 22;
int result = mainFibonacciSearch(arr, x);
if (result != -1) {
cout << "Found at index: " << result << endl;
} else {
cout << "Not found" << endl;
}
return 0;
}
import java.util.List;
public class FibonacciSearch {
public static int fibonacciSearch(List<Integer> arr, int x, int n, int fibM, int fibM_minus_1, int fibM_minus_2, int offset) {
/*
Recursive function to perform Fibonacci Search to find the index of 'x' in the sorted array 'arr' of size 'n'.
Args:
arr: Sorted list to search in.
x: Element to be searched.
n: Size of the list.
fibM: Current Fibonacci number (m'th).
fibM_minus_1: (m-1)'th Fibonacci number.
fibM_minus_2: (m-2)'th Fibonacci number.
offset: Eliminated range from the front of the array.
Returns:
Index of 'x' if found, otherwise -1.
*/
// Base case: If fibM becomes 0, element is not present
if (fibM == 0) {
return -1;
}
// Check if fibM_minus_2 is a valid location
int i = Math.min(offset + fibM_minus_2, n - 1);
// If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if (arr.get(i) < x) {
return fibonacciSearch(arr, x, n, fibM_minus_1, fibM_minus_2, fibM - fibM_minus_1, i);
}
// If x is less than the value at index fibM_minus_2, cut the subarray after i+1
else if (arr.get(i) > x) {
return fibonacciSearch(arr, x, n, fibM_minus_2, fibM - fibM_minus_1, fibM_minus_1 - fibM_minus_2, offset);
}
// Element found. Return index
else {
return i;
}
}
// Main function to initiate the Fibonacci Search
public static int mainFibonacciSearch(List<Integer> arr, int x) {
/*
This function initiates the recursive Fibonacci Search by calculating initial Fibonacci numbers.
Args:
arr: Sorted list to search in.
x: Element to be searched.
Returns:
Index of 'x' if found, otherwise -1.
*/
int n = arr.size();
int fibM_minus_2 = 0;
int fibM_minus_1 = 1;
int fibM = fibM_minus_1 + fibM_minus_2;
// Find the smallest Fibonacci number greater than or equal to n
while (fibM < n) {
fibM_minus_2 = fibM_minus_1;
fibM_minus_1 = fibM;
fibM = fibM_minus_1 + fibM_minus_2;
}
return fibonacciSearch(arr, x, n, fibM, fibM_minus_1, fibM_minus_2, -1);
}
public static void main(String[] args) {
List<Integer> arr = List.of(2, 3, 4, 10, 16, 22, 28, 35, 42, 50);
int x = 22;
int result = mainFibonacciSearch(arr, x);
if (result != -1) {
System.out.println("Found at index: " + result);
} else {
System.out.println("Not found");
}
}
}
#include <stdio.h>
int fibonacciSearch(int arr[], int x, int n, int fibM, int fibM_minus_1, int fibM_minus_2, int offset) {
/*
Recursive function to perform Fibonacci Search to find the index of 'x' in the sorted array 'arr' of size 'n'.
Args:
arr: Sorted array to search in.
x: Element to be searched.
n: Size of the array.
fibM: Current Fibonacci number (m'th).
fibM_minus_1: (m-1)'th Fibonacci number.
fibM_minus_2: (m-2)'th Fibonacci number.
offset: Eliminated range from the front of the array.
Returns:
Index of 'x' if found, otherwise -1.
*/
// Base case: If fibM becomes 0, element is not present
if (fibM == 0) {
return -1;
}
// Check if fibM_minus_2 is a valid location
int i = (offset + fibM_minus_2 < n - 1) ? offset + fibM_minus_2 : n - 1;
// If x is greater than the value at index fibM_minus_2, cut the subarray array from offset to i
if (arr[i] < x) {
return fibonacciSearch(arr, x, n, fibM_minus_1, fibM_minus_2, fibM - fibM_minus_1, i);
}
// If x is less than the value at index fibM_minus_2, cut the subarray after i+1
else if (arr[i] > x) {
return fibonacciSearch(arr, x, n, fibM_minus_2, fibM - fibM_minus_1, fibM_minus_1 - fibM_minus_2, offset);
}
// Element found. Return index
else {
return i;
}
}
// Main function to initiate the Fibonacci Search
int mainFibonacciSearch(int arr[], int x, int n) {
/*
This function initiates the recursive Fibonacci Search by calculating initial Fibonacci numbers.
Args:
arr: Sorted array to search in.
x: Element to be searched.
n: Size of the array.
Returns:
Index of 'x' if found, otherwise -1.
*/
int fibM_minus_2 = 0;
int fibM_minus_1 = 1;
int fibM = fibM_minus_1 + fibM_minus_2;
// Find the smallest Fibonacci number greater than or equal to n
while (fibM < n) {
fibM_minus_2 = fibM_minus_1;
fibM_minus_1 = fibM;
fibM = fibM_minus_1 + fibM_minus_2;
}
return fibonacciSearch(arr, x, n, fibM, fibM_minus_1, fibM_minus_2, -1);
}
int main() {
int arr[] = {2, 3, 4, 10, 16, 22, 28, 35, 42, 50};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 22;
int result = mainFibonacciSearch(arr, x, n);
if (result != -1) {
printf("Found at index: %d\n", result);
} else {
printf("Not found\n");
}
return 0;
}
Output:
Found at index: 5Frequently Asked Questions (FAQs) about Fibonacci Search
Q1. What is Fibonacci Search, and how does it work?
- Fibonacci Search is a speedy search algorithm for sorted arrays.
- It uses the Fibonacci sequence to efficiently narrow down the search by discarding large portions of the array in each step.
- This results in a fast search with a time complexity of O(log n).
Q2. What are the advantages and disadvantages of Fibonacci Search?
- Advantages:
- Efficient for large sorted arrays (O(log n) time complexity)
- Doesn’t require division operations, making it faster on certain architectures
- Disadvantages:
- Works only on sorted arrays
- Slightly more complex to implement than binary search
Q3. How does Fibonacci Search compare to binary search?
- Both Fibonacci and binary search offer efficient O(log n) search for sorted arrays. While Fibonacci Search avoids division, binary search is simpler. Choose based on hardware and your needs.
Q4. Can Fibonacci Search be applied to unsorted arrays?
- No, Fibonacci Search cannot be applied to unsorted arrays. It relies on the array being sorted to effectively eliminate sections in each step.
- If the array is unsorted, the comparison and elimination logic of Fibonacci Search would not work correctly.
Q5. Are there any real-world applications of Fibonacci Search?
While less common than binary search, Fibonacci Search has niche applications:
- Optimization: Finding optimal points in functions.
- Interpolation Search: Alternative for specific sorted arrays.
- Computer Networks: Error correction and data transmission (related to the Fibonacci sequence).
- Trading Strategies: (Limited use) Identifying potential support/resistance levels in markets.
Related topics:
