Depth First Search (DFS) and Breadth First Search (BFS)

By traversing a graph, we need to examine the vertices and edges of the graph. There are two standard methods for graph traversal. They are

Depth First Search (DFS)
Breadth First Search (BFS)

1. Depth First Search (DFS):

Depth First Search (DFS) is a graph traversal algorithm that explores a graph by going as deep as possible along each branch before backtracking.
It starts at a designated root node and visits as far as possible along each branch before backtracking to explore other unvisited neighbors.
DFS uses a stack data structure to keep track of the nodes to visit, adding a node to the stack when it’s discovered and removing it when all its neighbors are explored.

The following steps are performed to obtain the DFS traversal of a graph.

Step 1: Select any vertex for the starting point of the traversal. Visit that vertex and push it onto the stack.

Step 2: Select and visit an unvisited vertex from the top of the stack. Then push that vertex into the stack.

Step 3: Continue step 2 until the top vertex of the stack has no unvisited neighbors.

Step 4: If no unvisited neighbors remain, backtrack by popping a vertex from the stack.

Step 5: Continue the process of steps 2, 3, and 4 iteratively until there are no more vertices left in the stack to explore.

Ex:

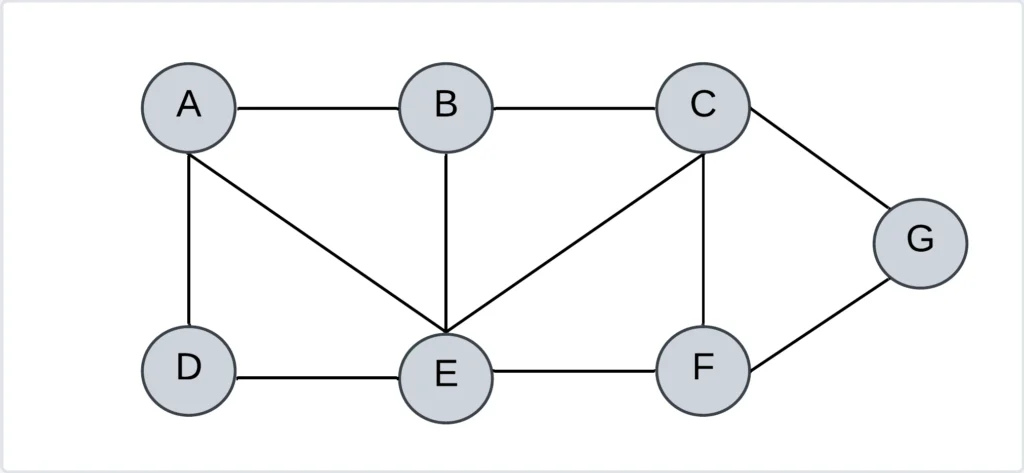
Step 1: Select the vertex A to start the traversal. Visit the vertex A and push that vertex into the stack.

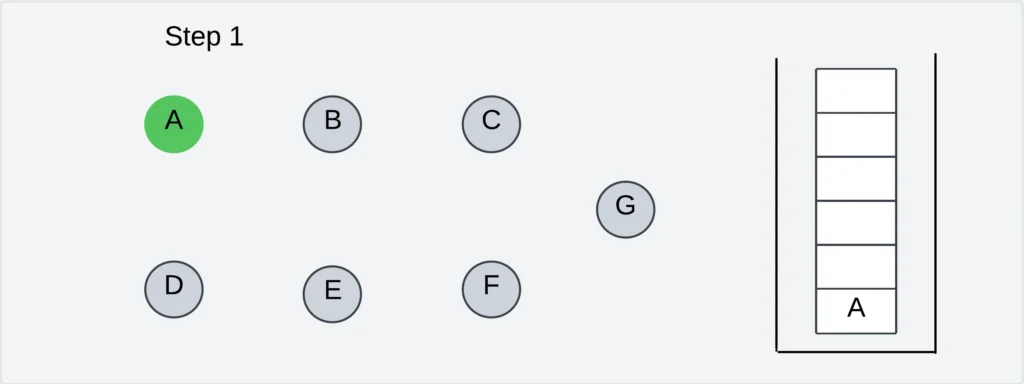
Step 2: Choose an unvisited neighbor of vertex A (from B, D, and E).

Let us visit vertex B

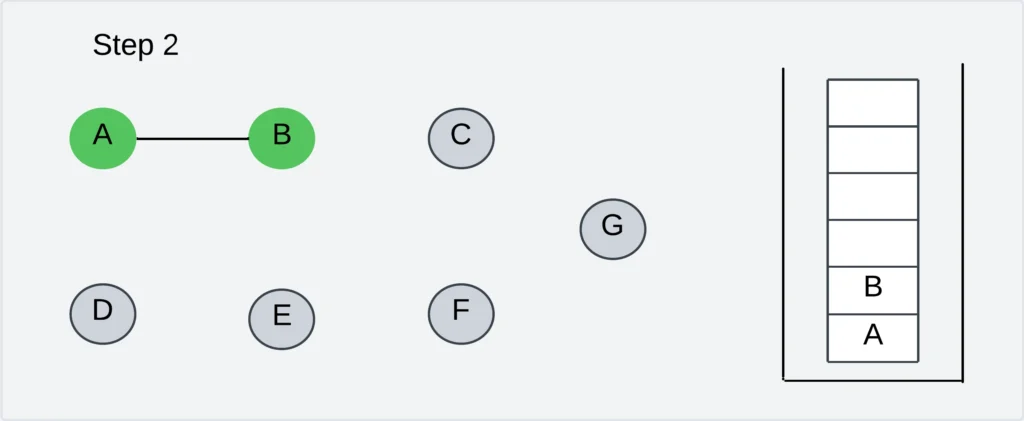
Step 3: Choose an unvisited neighbor of vertex B. The adjacent vertices are C and E. Let us visit the vertex C.

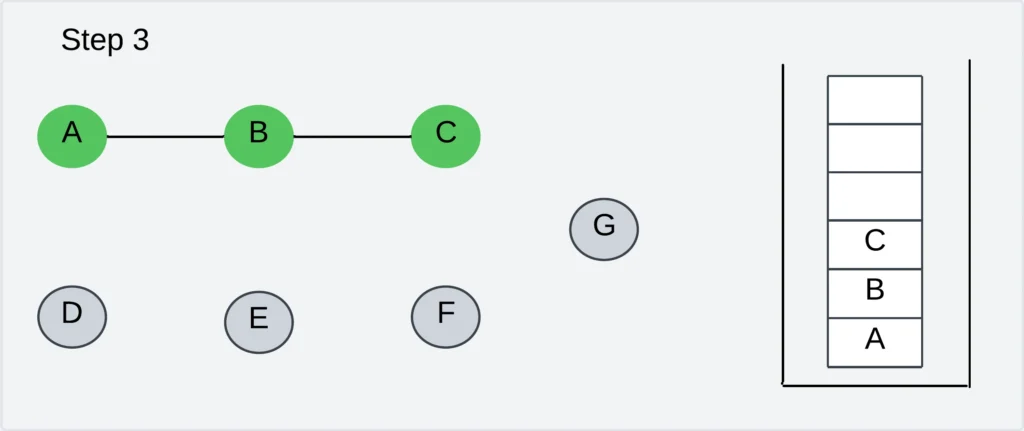
Step 4: Choose an unvisited neighbor of vertex C. The adjacent vertices are E, F, and G. Let us visit vertex E.

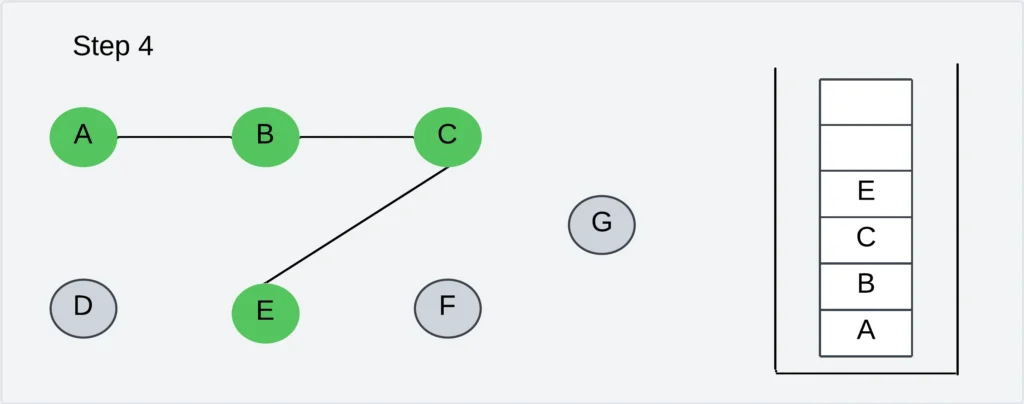
Step 5: Pick any unvisited vertex adjacent to E. The adjacent vertices are D and F. Let us visit the vertex D.

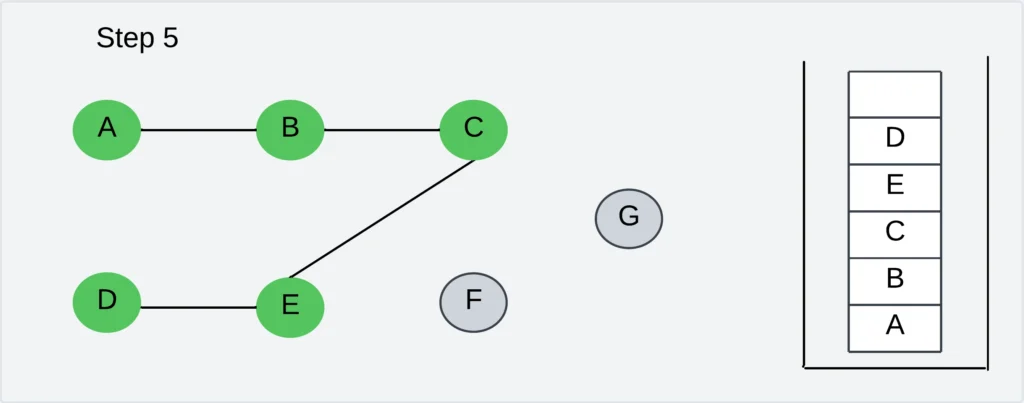
Step 6: Pick any unvisited vertex adjacent to D. There is no vertex to visit from D. so back trap from D to E and POP the vertex D.

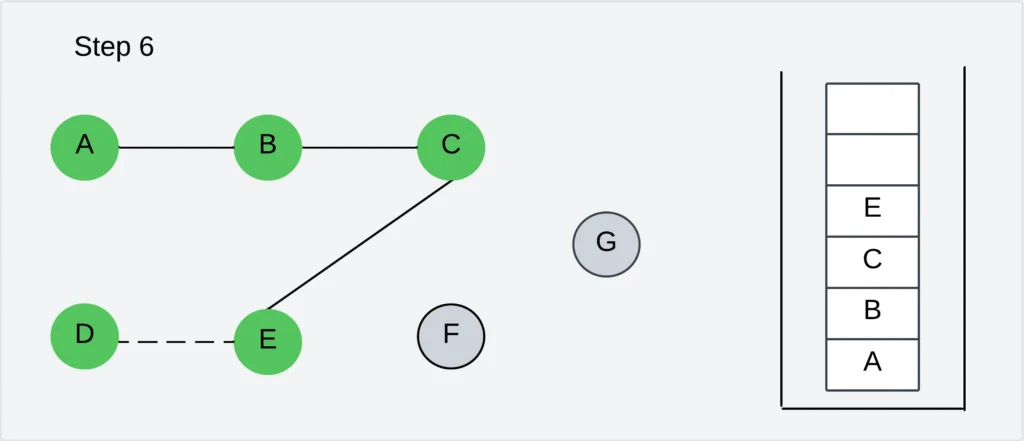
Step 7: Pick any unvisited vertex adjacent to E. The adjacent vertices are A, B, C, D, and F. Out of these the vertex F is not visited. Visit the vertex F and push into the stack.

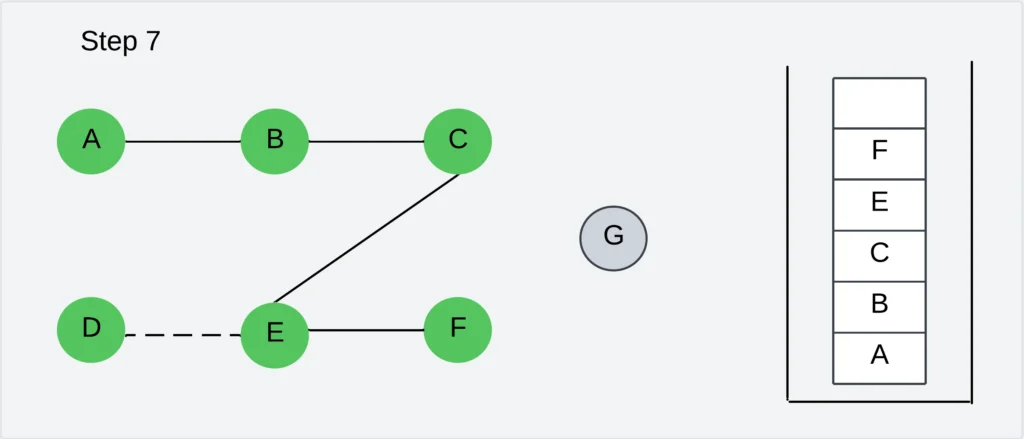
Step 8: Pick any unvisited vertex adjacent to F. The adjacent vertices are E, C, and G. Out of these vertex G is not visited. Visit the vertex G and push it into the stack.

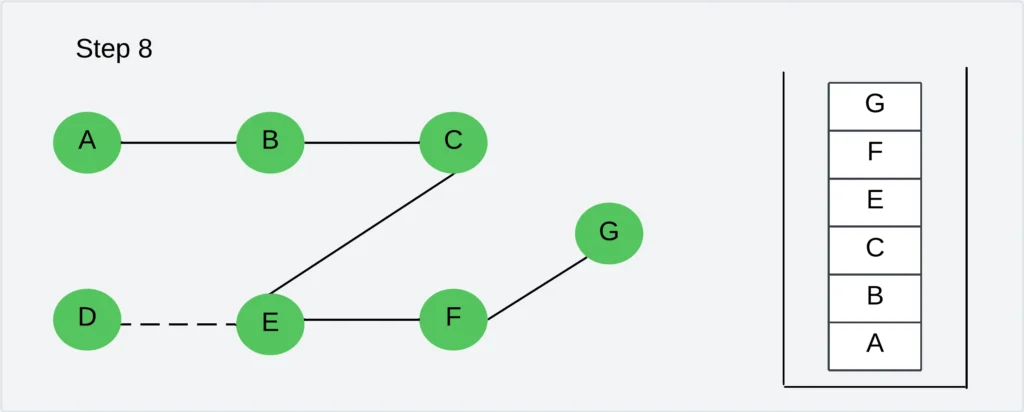
Step-9: Repeat step 8 and POP the respective vertices whose adjacent vertices are visited. The stack becomes empty.

2. Breadth First Search (BFS)

Breadth-First Search (BFS) is another graph traversal algorithm that explores a graph level by level. It starts at a root node and visits all the root’s immediate neighbors.
Then, for each of those neighbors, it visits their unvisited neighbors, and so on.
BFS uses a queue data structure to keep track of nodes to visit, ensuring that nodes at the same distance from the root are visited together.

The following steps are performed to obtain the BFS traversal of a graph.

Step 1: Select any vertex as the starting point for the traversal. Visit that vertex and add it to the queue.

Step 2: Visit all the adjacent vertices of the vertex at the front of the queue. Add any unvisited adjacent vertex to the queue.

Step 3: When there is no vertex to be visited from the vertex at the front of the queue then delete that vertex from the queue.

Step 4: Repeat steps 2 and 3 until the queue becomes empty.

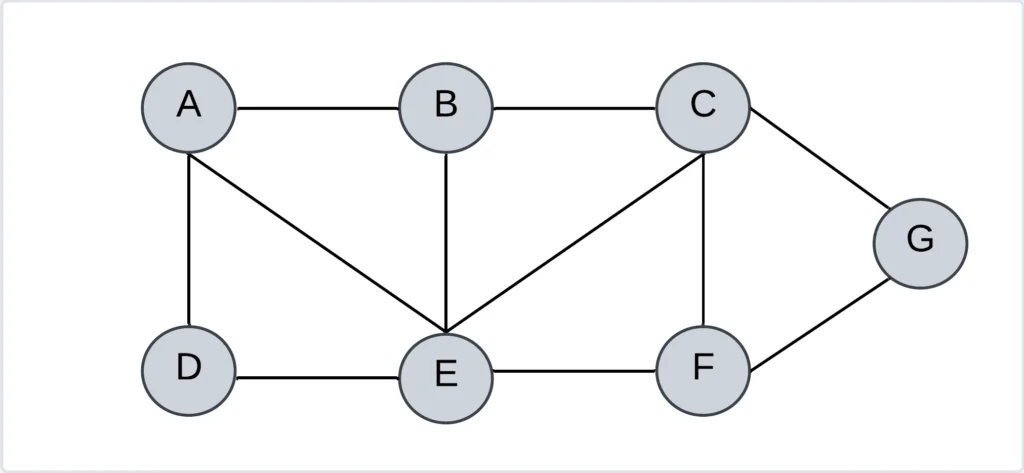
Example:

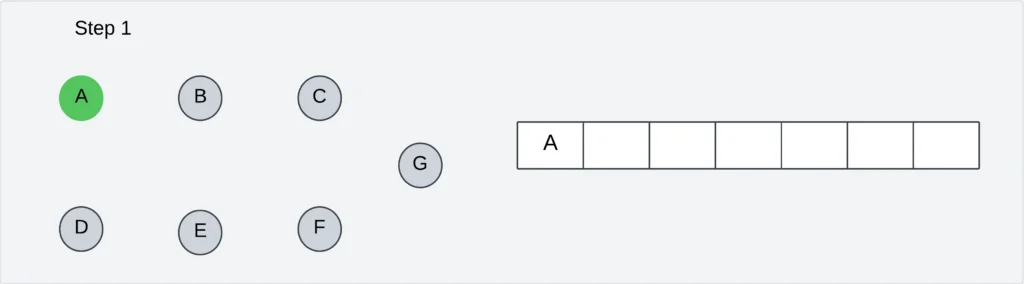
Step 1: Select the vertex A as the starting point of the traversal. Visit vertex A and insert it into the queue.

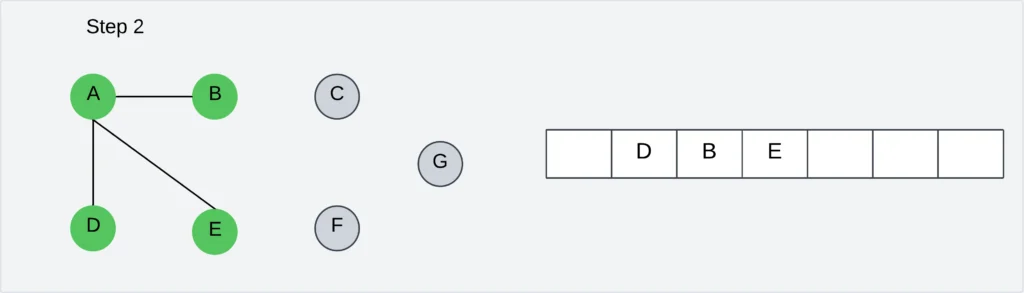
Step 2: Visit all unvisited neighbors of A: D, E, and B. Insert newly visited vertices into the queue and delete vertex A from the queue.

Step 3: Visit all unvisited neighbors of A. There is no vertex to visit. Delete the vertex D from the queue.

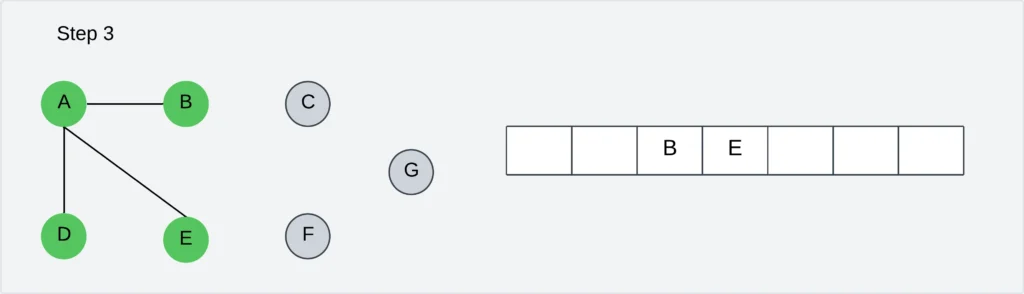
Step 4: Visit E’s unvisited neighbors, C and F. Insert newly visited vertices into the queue and delete the vertex E from the queue.

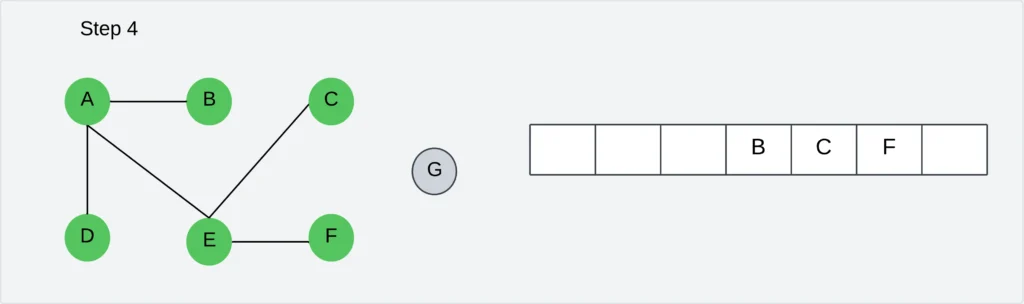
Step 5: Visit all unvisited neighbors of B. There is no vertex to visit. Delete the vertex B from the queue.

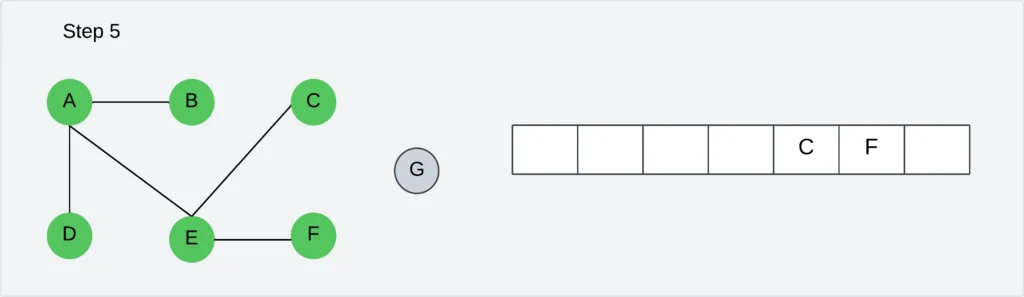
Step 6: Visit C’s unvisited neighbor, G. Insert newly visited vertices into the queue and delete vertex C from the queue.

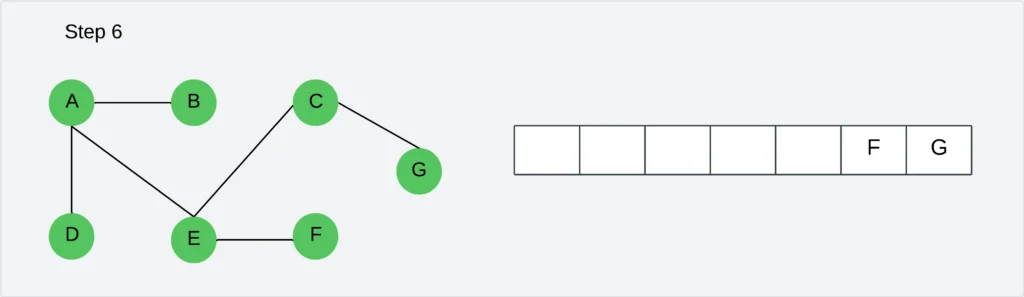
Step 7: Visit all unvisited neighbors of F. There is no vertex to visit. Delete the vertex F from the queue.

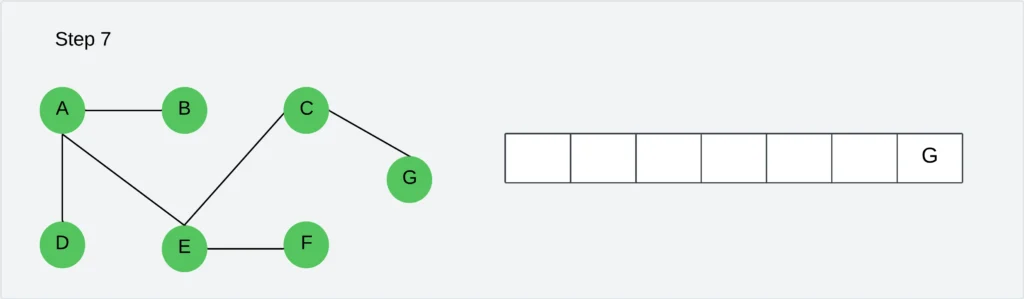
Step 8: Visit all unvisited neighbors of G. There is no vertex to visit. Delete the vertex G from the queue. So the Queue becomes empty.

1. What are the main differences between DFS and BFS?

The primary difference lies in the order they explore nodes:

Exploration Order: DFS prioritizes depth, going as far as possible along a branch before backtracking, while BFS explores level by level, visiting all neighbors at a given distance before moving to the next level.
Data Structure: DFS uses a stack (or recursion, which implicitly uses the call stack), while BFS uses a queue.
Applications: Depth-first search (DFS) is a valuable algorithm commonly employed for determining a topological order of nodes in a directed graph and identifying the presence of cycles within a graph.
Breadth-First Search (BFS) excels at finding the shortest paths in unweighted graphs and proves particularly useful in applications like peer-to-peer networks.

2. How do I choose between DFS and BFS for a problem?

The choice between DFS and BFS depends on the nature of the problem:

Shortest Path in Unweighted Graph: BFS always finds the shortest path in an unweighted graph, unlike DFS, which could find a longer one.
Exploring All Paths: DFS is a natural choice if you need to explore all possible paths from a source to a destination.
Topological Sorting: DFS is used for topological sorting, ordering vertices in a directed acyclic graph such that for every edge (u, v), vertex u comes before vertex v in the ordering.
Cycle Detection: Both DFS and BFS can be used for cycle detection, but DFS is often preferred due to its lower space complexity in some cases.

3. What is the time and space complexity of DFS and BFS?

Both DFS and BFS have similar time and space complexities:

Time Complexity: In the worst case, both algorithms visit every vertex and every edge once, resulting in a time complexity of O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity: Both algorithms store visited nodes, and in the worst case (for example, a skewed tree), they might store all vertices, leading to a space complexity of O(V). However, the space used can vary depending on the graph’s structure and the implementation details.

4. Can DFS find the shortest path in a graph?

Although DFS can locate a route between two nodes in an unweighted graph, it doesn’t necessarily identify the shortest route.
Depth-first search (DFS) delves deeply into a single path before exploring other options. Consequently, even if it finds a path to the destination, it may not be the shortest one.
In an unweighted graph, breadth-first search (BFS) systematically explores the graph level by level, ensuring the identification of the shortest path based on the number of edges.

5. How does DFS handle cycles in a graph?

DFS can detect cycles in a graph. The key is to keep track of visited nodes and the nodes currently on the recursion stack.
In depth-first search (DFS), encountering a node already on the recursion stack reveals a cycle within the graph.
To avoid getting stuck in an infinite loop, DFS marks nodes as visited and only explores unvisited nodes.

6. What are some real-world applications of BFS?

Breadth-First Search has many practical applications:

Social Networks: Finding the shortest number of connections between two people.
Network Broadcasting: Broadcasting a message to all devices on a network efficiently.
Garbage Collection (Cheney’s Algorithm): Finding reachable objects in memory to reclaim unused memory.
Web Crawlers: Crawling web pages by following links level by level from a starting page.
Finding paths in AI (e.g., finding paths in a game): Exploring possible moves or states level by level to find the optimal solution.

Table of Contents