Introduction to Bubble Sort Algorithm
Bubble Sort is also known as exchange sort. Bubble sorting is a simple sorting method. Bubble sort is based on the comparison method. In this soring, it sorts the array elements by repeatedly moving the largest element to the highest index position of the array.
In the sorting, each pair of adjacent elements are compared and the elements are supported if they are not in order. This process will continue till the list of unsorted elements is exhausted.
This sorting procedure is called bubble sorting because elements “bubble” to the top of the list.
Note: This type of sorting does not suit when the value of n is large.
Table of Contents
Algorithm of Bubble Sort
- Start: Begin with the first element of the list.
- Compare: Compare the current element with the next element.
- Exchange (if required): If the current element possesses a greater value than the succeeding element, interchange their respective positions.
- Move Forward: Move to the next element.
- Repeat: Iterate through steps 2-4 continuously until the conclusion of the list is reached. This constitutes a single “pass” of the algorithm.
- Check for Swaps: After each pass, check if any swaps were made.
- If swaps were made: The list is not yet sorted. Go back to step 1 and start another pass.
- If no swaps were made: The list is sorted. Stop the algorithm.
Pseudocode:
function bubbleSort(list): n = length(list) for i = 0 to n-1: swapped = false for j = 0 to n-i-1: if list[j] > list[j+1]: swap(list[j], list[j+1]) swapped = true if not swapped: break // Early exit if no swaps were made in a pass
Explanation:
- The outer loop (i) controls the number of passes.
- The inner loop (j) compares and swaps adjacent elements within each pass.
- The swapped flag is used to optimize the algorithm. A pass devoid of swaps signifies a sorted list, permitting the algorithm to terminate ahead of schedule.
Working of Bubble Sort with an example
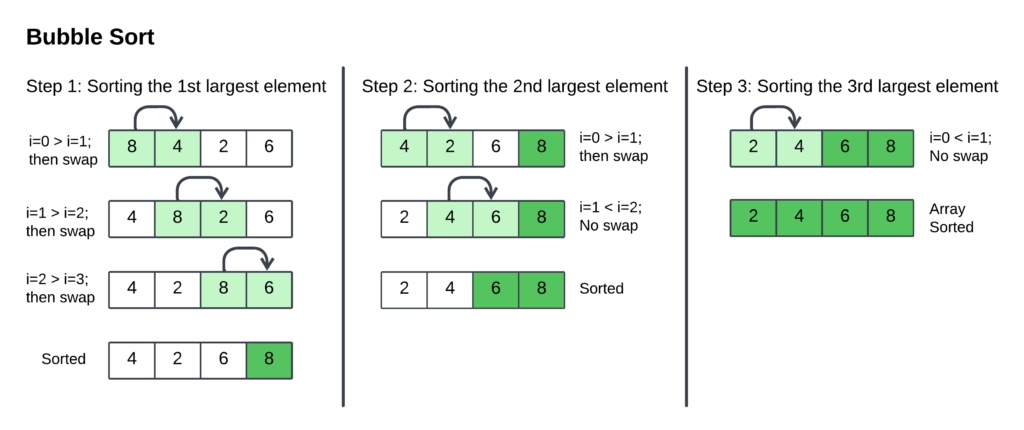
The bubble sort process is on a list of four numbers: 8, 4, 2, and 6.
Step 1: Sorting the 1st Largest Element
- Iteration 1 (i = 0):
- Compare the first two elements (8 and 4). Since 8 > 4, swap their positions. The list becomes 4, 8, 2, 6.
- Compare the next pair (8 and 2). Swap them as 8 > 2. The list is now: 4, 2, 8, 6.
- Compare the last pair (8 and 6). Swap again, resulting in 4, 2, 6, 8. Notice that the largest element (8) has “bubbled up” to the end of the list.
- Iteration 2 (i = 1):
- Compare the first two (4 and 2). Swap since 4 > 2. The list is: 2, 4, 6, 8.
- Compare the next pair (4 and 6). No swap is needed.
- The third element (6) is already in its correct position.
- Iteration 3 (i = 2):
- Compare the first two (2 and 4). No swap is needed.
- The list is now sorted: 2, 4, 6, 8.
Step 2: Sorting the 2nd Largest Element
- Iteration 1 (i = 0):
- Compare the first two (2 and 4). No swap is needed.
- Compare the next pair (4 and 6). No swap is needed.
- The list is already sorted (no swaps made).
Step 3: Sorting the 3rd Largest Element
- Iteration 1 (i = 0):
- Compare the first two (2 and 4). No swap is needed.
The list is already sorted (no swaps made).
Bubble Sort Program Implementation
def bubble_sort(arr):
n = len(arr) # Get the length of the input array
# Outer loop: Iterate over each element in the array
for i in range(n):
# Optimization: Track if swaps were made in this pass
swapped = False
# Inner loop: Compare and swap adjacent elements
for j in range(0, n - i - 1):
# If the current element is larger than the next, swap them
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
# Optimization: If no swaps occurred in this pass, the array is sorted
if not swapped:
break # Exit the outer loop
# Example usage
data = [5, 1, 4, 2, 8]
bubble_sort(data)
print("Sorted array:", data)
#include <iostream>
#include <vector>
using namespace std;
void bubbleSort(vector<int>& arr) {
int n = arr.size(); // Get the size of the input vector
// Outer loop: Iterate over each element in the vector
for (int i = 0; i < n; i++) {
// Optimization: Track if swaps were made in this pass
bool swapped = false;
// Inner loop: Compare and swap adjacent elements
for (int j = 0; j < n - i - 1; j++) {
// If the current element is larger than the next, swap them
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
swapped = true;
}
}
// Optimization: If no swaps occurred in this pass, the vector is sorted
if (!swapped) {
break; // Exit the outer loop
}
}
}
int main() {
vector<int> data = {5, 1, 4, 2, 8};
bubbleSort(data);
cout << "Sorted array: ";
for (int num : data) {
cout << num << " ";
}
cout << endl;
return 0;
}
import java.util.Arrays;
public class BubbleSort {
public static void bubbleSort(int[] arr) {
int n = arr.length; // Get the length of the input array
// Outer loop: Iterate over each element in the array
for (int i = 0; i < n; i++) {
// Optimization: Track if swaps were made in this pass
boolean swapped = false;
// Inner loop: Compare and swap adjacent elements
for (int j = 0; j < n - i - 1; j++) {
// If the current element is larger than the next, swap them
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// Optimization: If no swaps occurred in this pass, the array is sorted
if (!swapped) {
break; // Exit the outer loop
}
}
}
public static void main(String[] args) {
int[] data = {5, 1, 4, 2, 8};
bubbleSort(data);
System.out.println("Sorted array: " + Arrays.toString(data));
}
}
#include <stdio.h>
#include <stdbool.h> // For boolean data type
void bubbleSort(int arr[], int n) {
// Outer loop: Iterate over each element in the array
for (int i = 0; i < n; i++) {
// Optimization: Track if swaps were made in this pass
bool swapped = false;
// Inner loop: Compare and swap adjacent elements
for (int j = 0; j < n - i - 1; j++) {
// If the current element is larger than the next, swap them
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// Optimization: If no swaps occurred in this pass, the array is sorted
if (!swapped) {
break; // Exit the outer loop
}
}
}
int main() {
int data[] = {5, 1, 4, 2, 8};
int n = sizeof(data) / sizeof(data[0]); // Calculate the size of the array
bubbleSort(data, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", data[i]);
}
printf("\n");
return 0;
}
Output:
Sorted array: [1, 2, 4, 5, 8]
Bubble Sort Complexity Analysis:
| Bubble Sort Complexity | Best Case | Average Case | Worst Case |
| Time Complexity | O(n) | O(n^2) | O(n^2) |
| Auxiliary Space | O(1) | O(1) | O(1) |
| Space Complexity | O(1) | O(1) | O(1) |
How to Optimize Bubble Sort
Key Optimization Techniques:
- Early Termination (Flag Variable):
- Concept: Introduce a boolean flag variable (e.g., swapped) to track if any swaps were made during a pass.
- Implementation:
- Initialize the flag to true at the beginning of each pass.
- If a swap occurs during the pass, set the flag to false.
- After the pass, check the flag. If it’s still true (no swaps were made), the list is sorted, and the algorithm can terminate early.
- Why it works: If no swaps are needed in a pass, it guarantees that the list is fully sorted.
- Modified Inner Loop:
- Concept: In each pass of the Bubble Sort, the largest element always ends at the end of the unsorted portion.
- Implementation: Shrink the inner loop’s range with each pass. Instead of iterating till the end of the list every time, iterate only up to the last unsorted position.
- Why it works: It avoids unnecessary comparisons and swaps for elements already in their correct positions.
Optimized Bubble Sort Pseudocode:
function bubbleSortOptimized(list): n = length(list) for i = 0 to n-1: swapped = false for j = 0 to n-i-1: if list[j] > list[j+1]: swap(list[j], list[j+1]) swapped = true if not swapped: break // Early exit if no swaps were made in a pass
Advantages of Bubble Sort
- Easy to understand and implement.
- Minimal extra memory usage.
Disadvantages of Bubble Sort
- Not efficient for large datasets due to its quadratic time complexity.
- In practical use cases, the quadratic time complexity of Bubble Sort makes it less desirable than more efficient algorithms such as Quicksort or Merge Sort
What are the Alternatives to Bubble Sort
Bubble Sort has several alternatives in DSA, each with its strengths:
- Efficient Sorting (Large Datasets): Quicksort, Merge Sort, Heap Sort (average O(n log n) time complexity).
- Simple Sorting (Small Datasets): Insertion Sort, Selection Sort (good for nearly sorted data).
- Specialized Sorting: Counting Sort (integers within a range), Radix Sort (fixed-length digits).
- Hybrid Sorting: Timsort (combines Merge Sort and Insertion Sort), Introsort (combines Quicksort, Heap Sort, and Insertion Sort).
Related FAQs on Bubble Sort Algorithm
Q1. Is Bubble Sort a recursive algorithm?
- No, Bubble Sort is typically implemented iteratively using loops. While it’s possible to implement it recursively, it’s generally less efficient and not the standard approach.
Q2. Can Bubble Sort be used for linked lists?
- Yes, Bubble Sort can be adapted to work with linked lists. Instead of swapping elements by index, you would modify the links between nodes to rearrange them in the sorted order.
Q3. Are there any real-world applications of Bubble Sort?
- While Bubble Sort isn’t used for large datasets due to its inefficiency, it does have some niche applications:
- Educational Tool: It’s a great teaching aid to introduce sorting concepts.
- Small Datasets: Bubble Sort can be a practical option for Tiny datasets, where its performance limitations are not a significant concern.
- Graphics: It’s sometimes used in computer graphics for tasks like polygon filling, where almost-sorted arrays need minor adjustments.
Q4. When should you use Bubble Sort?
- Bubble Sort is primarily used for educational purposes to demonstrate how sorting algorithms work.
- It can also be suitable for small datasets where efficiency is not a primary concern.
- When dealing with larger datasets, it is advisable to employ more performant sorting algorithms like Quicksort or Merge Sort..
Q5. Is Bubble Sort stable?
- Yes, Bubble Sort is a stable sorting algorithm. This means that if two elements have the same value, their relative order in the original list is preserved in the sorted list.
Related topics:
