Binary Tree in Data Structure – Types | Implementation

• A binary tree allows each node to have at most two children: a left child and a right child.
•  As a result, the binary tree has order 2.
• A binary tree can be either empty or have the following nodes:
  • a) the root node
  • b) The subtrees on the left and right are also binary trees.
• A binary tree is a finite collection of nodes that can be empty or have two distinct trees, the left and right sub-trees, and a root.
• Each node in a binary tree will contain two pointer fields to indicate the sub-branches and one data field.
• Every node in the binary tree will have a maximum of two degrees.

Binary Tree Types: 

Three different kinds of binary trees exist:

1. Left-skewed binary tree: 

• A tree is said to be left-skewed if every node lacks the correct sub-tree.

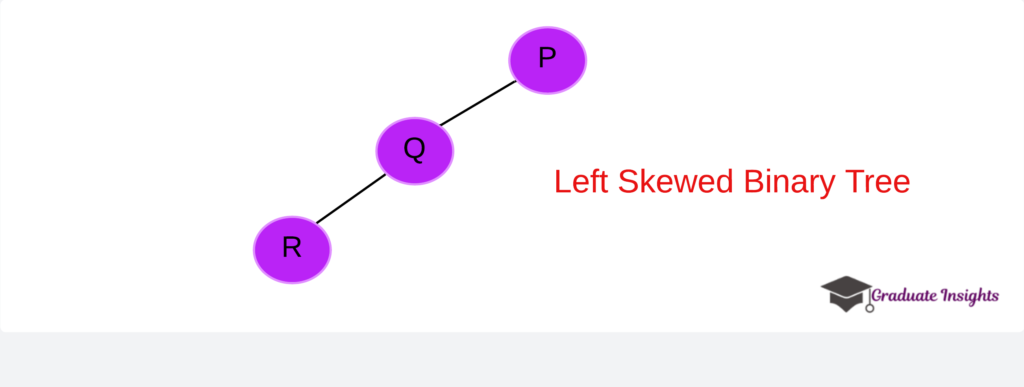
2. Right-skewed binary tree:

• We refer to a tree’s right sub-tree if its left sub-tree is absent from every node.

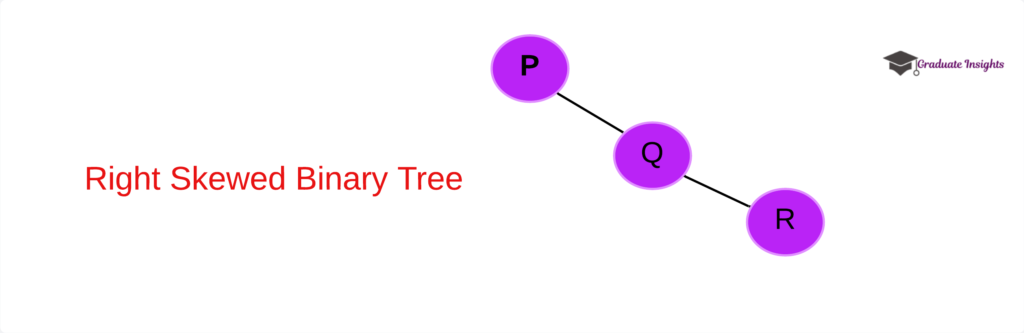
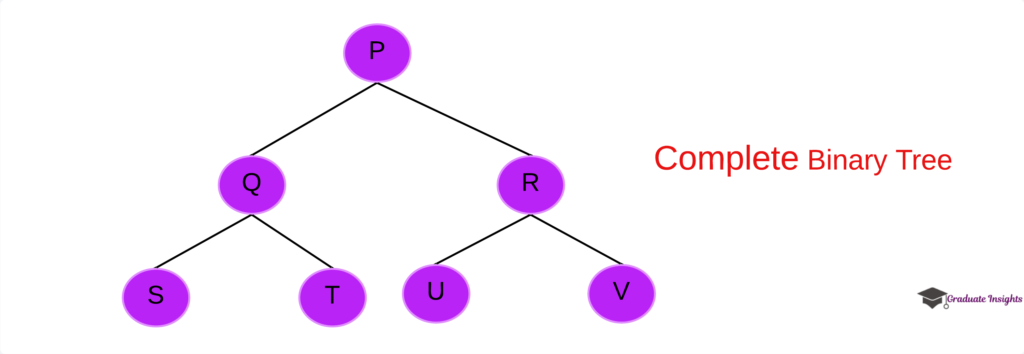
3. Complete binary tree:

• A full binary tree is one in which each node has a degree of no more than two. 
• There is precisely one node at level 0, two nodes at level 1, four nodes at level 2, and so on in a full binary tree.
• Definitively, in a full binary tree of depth d, each level l (from 0 to d) contains exactly 2^l nodes.

Note:

1. A binary tree with n depth can have a maximum of 2ⁿ -1 nodes.
2. A level l binary tree will have a maximum of 2L nodes at each level, where L begins at 0.
3. A binary tree with n nodes will have at most n+1 null branches.
4. A full binary tree with n terminal nodes has 2(n-1) edges in total.

Representation of Binary Tree

There are two primary methods for representing a binary tree: 

1. Sequential Representation; and 
2. Linked Representation.

1.  The Sequential Representation

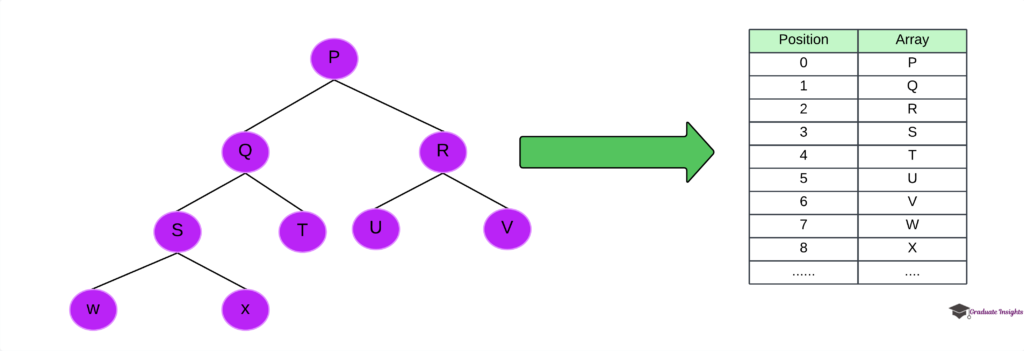
• Sequential representation using a one-dimensional array is the most straightforward method of storing binary trees in memory.

1. The first position of the array contains the binary tree’s root.
2. A node’s left child is in position 2J+1 and its right child is in place 2J+2 if it is in the jth location of the array.

• A tree can be stored in an array up to a maximum size of 2^(d+1)-1, where d is the tree’s depth.

Benefits of sequential representation: 

• The only benefit of this kind of representation is that it allows for direct access to any node and quick identification of a node’s parent or left children due to random access.

Sequential representation’s drawbacks:

1. Memory waste is the main drawback of this kind of representation. For instance, half of the array is unused in the skewed tree.
2. The maximum depth of the tree in this kind of representation must be set. The array size has already been determined. Memory will be wasted if the array size is selected to be significantly bigger than the tree’s depth. Furthermore, we won’t be able to depict some portions of the tree if we choose an array size smaller than the tree’s depth.
3. Any node added or removed from the tree will incur additional costs since other nodes must be moved to the proper locations to maintain the binary tree’s meaning.
4. We should seek a more flexible representation, as this sequential approach has limitations. Thus, we will use a linked list instead of an array to represent the tree.

Program implementation of the sequential representation in binary tree

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
def create_tree(tree_list):
    """
    Creates a binary tree from a sequential representation (list).
    Args:
        tree_list: A list representing the binary tree. 
                     - None represents an empty node.
                     - Values are stored level-order (BFS).
    Returns:
        The root node of the created binary tree.
    """
    if not tree_list or tree_list[0] is None:
        return None
    root = Node(tree_list[0])
    queue = [root]  # Use a queue for level-order traversal
    i = 1  
    while queue and i < len(tree_list):
        curr_node = queue.pop(0)
        # Left child
        if i < len(tree_list) and tree_list[i] is not None:
            curr_node.left = Node(tree_list[i])
            queue.append(curr_node.left) 
        i += 1
        # Right child
        if i < len(tree_list) and tree_list[i] is not None:
            curr_node.right = Node(tree_list[i])
            queue.append(curr_node.right)
        i += 1
    return root
# Example usage:
tree_data = [1, 2, 3, 4, None, 5, None, None, None, 6, 7]
root = create_tree(tree_data) 
# (Optional) Function to print the tree (for verification)
def print_tree(root):
    if root:
        print(root.data, end=" ")
        print_tree(root.left)
        print_tree(root.right)
print_tree(root) # Output: 1 2 4 6 7 3 5 

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct Node {
    int data;
    Node *left, *right;
    Node(int data) : data(data), left(nullptr), right(nullptr) {} 
};
Node* createTree(const vector<int>& treeList) {
    """
    Creates a binary tree from a sequential representation (vector).
    Args:
        treeList: A vector representing the binary tree. 
                     - -1 represents an empty node.
                     - Values are stored level-order (BFS).
    Returns:
        The root node of the created binary tree.
    """
    if (treeList.empty() || treeList[0] == -1) {
        return nullptr;
    }
    Node* root = new Node(treeList[0]);
    queue<Node*> q; 
    q.push(root); 
    int i = 1;
    while (!q.empty() && i < treeList.size()) {
        Node* currNode = q.front();
        q.pop();
        // Left child
        if (i < treeList.size() && treeList[i] != -1) {
            currNode->left = new Node(treeList[i]);
            q.push(currNode->left);
        }
        i++; 
        // Right child
        if (i < treeList.size() && treeList[i] != -1) {
            currNode->right = new Node(treeList[i]);
            q.push(currNode->right);
        }
        i++;
    }
    return root;
}
// (Optional) Function to print the tree (for verification)
void printTree(Node* root) {
    if (root) {
        cout << root->data << " ";
        printTree(root->left);
        printTree(root->right);
    }
}
int main() {
    vector<int> treeData = {1, 2, 3, 4, -1, 5, -1, -1, -1, 6, 7};
    Node* root = createTree(treeData);
    printTree(root); // Output: 1 2 4 6 7 3 5 
    cout << endl;
    return 0;
}

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
class Node {
    int data;
    Node left, right;
    Node(int data) {
        this.data = data;
        left = null;
        right = null;
    }
}
public class BinaryTreeFromSequential {
    public static Node createTree(ArrayList<Integer> treeList) {
        """
        Creates a binary tree from a sequential representation (ArrayList).
        Args:
            treeList: An ArrayList representing the binary tree. 
                        - -1 represents an empty node.
                        - Values are stored level-order (BFS).
        Returns:
            The root node of the created binary tree.
        """
        if (treeList.isEmpty() || treeList.get(0) == -1) {
            return null;
        }
        Node root = new Node(treeList.get(0));
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        int i = 1;
        while (!queue.isEmpty() && i < treeList.size()) {
            Node currNode = queue.poll(); 
            // Left child
            if (i < treeList.size() && treeList.get(i) != -1) {
                currNode.left = new Node(treeList.get(i));
                queue.add(currNode.left);
            }
            i++;
            // Right child
            if (i < treeList.size() && treeList.get(i) != -1) {
                currNode.right = new Node(treeList.get(i));
                queue.add(currNode.right);
            }
            i++;
        }
        return root;
    }
    // (Optional) Function to print the tree (for verification)
    public static void printTree(Node root) {
        if (root != null) {
            System.out.print(root.data + " ");
            printTree(root.left);
            printTree(root.right);
        }
    }
    public static void main(String[] args) {
        ArrayList<Integer> treeData = new ArrayList<>();
        treeData.add(1);
        treeData.add(2);
        treeData.add(3);
        treeData.add(4);
        treeData.add(-1);
        treeData.add(5);
        treeData.add(-1);
        treeData.add(-1);
        treeData.add(-1);
        treeData.add(6);
        treeData.add(7);
        Node root = createTree(treeData);
        printTree(root);  // Output: 1 2 4 6 7 3 5 
        System.out.println(); 
    }
}

#include <stdio.h>
#include <stdlib.h>
// Node structure for the binary tree
struct Node {
    int data;
    struct Node *left, *right;
};
// Structure for queue nodes (used in level-order traversal)
struct QueueNode {
    struct Node* treeNode;
    struct QueueNode* next;
};
// Structure for the queue itself
struct Queue {
    struct QueueNode* front, * rear;
};
// Function to create a new queue node
struct QueueNode* newNode(struct Node* treeNode) {
    struct QueueNode* temp = (struct QueueNode*)malloc(sizeof(struct QueueNode));
    temp->treeNode = treeNode;
    temp->next = NULL;
    return temp;
}
// Function to create a new queue
struct Queue* createQueue() {
    struct Queue* q = (struct Queue*)malloc(sizeof(struct Queue));
    q->front = q->rear = NULL;
    return q;
}
// Function to enqueue a tree node into the queue
void enqueue(struct Queue* q, struct Node* treeNode) {
    struct QueueNode* temp = newNode(treeNode);
    // If queue is empty, new node is both front and rear
    if (q->rear == NULL) {
        q->front = q->rear = temp;
        return;
    }
    // Add the new node at the end of the queue and change rear
    q->rear->next = temp;
    q->rear = temp;
}
// Function to dequeue a tree node from the queue
struct Node* dequeue(struct Queue* q) {
    // If queue is empty, return NULL
    if (q->front == NULL) {
        return NULL;
    }
    // Store previous front and move front one node ahead
    struct QueueNode* temp = q->front;
    q->front = q->front->next;
    // If front becomes NULL, then the queue is empty
    if (q->front == NULL) {
        q->rear = NULL;
    }
    struct Node* node = temp->treeNode; 
    free(temp);
    return node;
}
// Function to create a binary tree from a sequential representation (array)
struct Node* createTree(int treeData[], int size) {
    """
    Creates a binary tree from a sequential representation (array).
    Args:
        treeData: An array representing the binary tree. 
                  - -1 represents an empty node.
                  - Values are stored level-order (BFS).
        size: The size of the treeData array.
    Returns:
        The root node of the created binary tree.
    """
    if (size == 0 || treeData[0] == -1) {
        return NULL;
    }
    struct Node* root = (struct Node*)malloc(sizeof(struct Node));
    root->data = treeData[0];
    root->left = root->right = NULL;
    struct Queue* q = createQueue();
    enqueue(q, root); 
    int i = 1;
    while (! (q->front == NULL)  && i < size) {
        struct Node* currNode = dequeue(q); 
        // Left child
        if (i < size && treeData[i] != -1) {
            currNode->left = (struct Node*)malloc(sizeof(struct Node));
            currNode->left->data = treeData[i];
            currNode->left->left = currNode->left->right = NULL;
            enqueue(q, currNode->left); 
        }
        i++;
        // Right child
        if (i < size && treeData[i] != -1) {
            currNode->right = (struct Node*)malloc(sizeof(struct Node));
            currNode->right->data = treeData[i];
            currNode->right->left = currNode->right->right = NULL;
            enqueue(q, currNode->right); 
        }
        i++;
    }
    return root;
}
// (Optional) Function to print the tree (for verification)
void printTree(struct Node* root) {
    if (root != NULL) {
        printf("%d ", root->data);
        printTree(root->left);
        printTree(root->right);
    }
}
int main() {
    int treeData[] = {1, 2, 3, 4, -1, 5, -1, -1, -1, 6, 7};
    int size = sizeof(treeData) / sizeof(treeData[0]);
    struct Node* root = createTree(treeData, size);
    printTree(root); // Output: 1 2 4 6 7 3 5 
    printf("\n");
    return 0;
}

Output:

1 2 4 3 5 6 7 
        1
      /   \
     2     3
    / \     \
   4   None   5
  / \
 6   7 

2. Linked Representation of Binary Tree

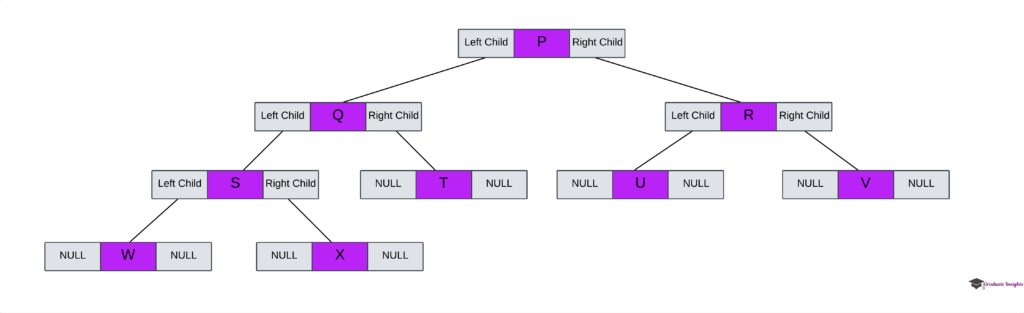
• Pointers are used to create a linked representation of trees in memory. 
• A node in a linked representation includes two pointers for the left and right child as one information field since each node in a binary tree may only have a maximum of two children. 
• The appropriate pointer field is NULL if a node has no children.

Benefits of linked representation: 

1. Since there is no memory waste, this representation is better than our array representation. The tree’s depth doesn’t need to be known in advance. Using dynamic memory, one can create as many memory nodes as needed. In the rare case that certain nodes are no longer required, they can be deleted by making their addresses available.
2. The most frequent operations, insertions, and deletions, may be carried out without relocating the nodes.

The drawbacks of linked representation

1. Special methods are needed to access a node directly using this format.
2. This structure necessitates additional memory per node to accommodate the left and right subtree references.

Program implementation of the sequential representation in binary tree

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None  # Left child
        self.right = None  # Right child
def create_linked_tree(data_list):
    """
    Creates a binary tree using a linked representation from a list.
    Args:
        data_list: A list of values where:
                   - -1 represents an empty node.
                   - The list order does not strictly imply tree structure.
                   - You will likely need additional information to determine
                     the connections between nodes (e.g., from user input).
    Returns:
        The root of the created binary tree (or None if the list is empty).
    """
    if not data_list:
        return None
    nodes = [Node(data) if data != -1 else None for data in data_list]
    # Example logic to connect nodes (you'll need to adapt this):
    # Assuming data_list represents a level-order traversal, 
    # and you are provided with parent-child relationships separately. 
    n = len(nodes)
    for i in range(n):
        if nodes[i] is not None:
            left_child_index = 2 * i + 1
            right_child_index = 2 * i + 2
            if left_child_index < n:
                nodes[i].left = nodes[left_child_index]
            if right_child_index < n:
                nodes[i].right = nodes[right_child_index]
    return nodes[0]  # Return the root node 
# Example usage:
data = [1, 2, 3, 4, -1, 5, -1, -1, -1, 6, 7]
root = create_linked_tree(data)
# (Optional) Function to print the tree in-order (for verification)
def inorder_traversal(node):
    if node:
        inorder_traversal(node.left)
        print(node.data, end=" ")
        inorder_traversal(node.right)
inorder_traversal(root)  # Output will depend on how you connect nodes 

#include <iostream>
#include <vector>
using namespace std;
struct Node {
    int data;
    Node *left, *right;
    Node(int data) : data(data), left(nullptr), right(nullptr) {}
};
Node* createLinkedTree(const vector<int>& dataList) {
    """
    Creates a binary tree using a linked representation from a vector.
    Args:
        dataList: A vector of values where:
                   - -1 represents an empty node.
                   - The vector order does not strictly imply tree structure.
                   - You will likely need additional information to determine
                     the connections between nodes (e.g., from user input).
    Returns:
        The root of the created binary tree (or nullptr if the vector is empty).
    """
    if (dataList.empty()) {
        return nullptr;
    }
    vector<Node*> nodes;
    for (int data : dataList) {
        if (data != -1) {
            nodes.push_back(new Node(data));
        } else {
            nodes.push_back(nullptr); 
        }
    }
    // Example logic to connect nodes (you'll need to adapt this):
    // Assuming dataList represents a level-order traversal, 
    // and you are provided with parent-child relationships separately.
    int n = nodes.size();
    for (int i = 0; i < n; ++i) {
        if (nodes[i] != nullptr) {
            int leftChildIndex = 2 * i + 1;
            int rightChildIndex = 2 * i + 2;
            if (leftChildIndex < n) {
                nodes[i]->left = nodes[leftChildIndex];
            }
            if (rightChildIndex < n) {
                nodes[i]->right = nodes[rightChildIndex];
            }
        }
    }
    return nodes[0]; 
}
// (Optional) Function to print the tree in-order (for verification)
void inorderTraversal(Node* node) {
    if (node) {
        inorderTraversal(node->left);
        cout << node->data << " ";
        inorderTraversal(node->right);
    }
}
int main() {
    vector<int> data = {1, 2, 3, 4, -1, 5, -1, -1, -1, 6, 7};
    Node* root = createLinkedTree(data);
    inorderTraversal(root); // Output will depend on how you connect nodes 
    cout << endl;
    // Remember to deallocate the dynamically allocated tree nodes
    // (not shown here for brevity, but essential to avoid memory leaks).
    return 0;
}

import java.util.ArrayList;
class Node {
    int data;
    Node left, right;
    Node(int data) {
        this.data = data;
        left = null;
        right = null;
    }
}
public class LinkedBinaryTree {
    public static Node createLinkedTree(ArrayList<Integer> dataList) {
        """
        Creates a binary tree using a linked representation from an ArrayList.
        Args:
            dataList: An ArrayList of values where:
                       - -1 represents an empty node.
                       - The ArrayList order does not strictly imply tree structure.
                       - You will likely need additional information to determine
                         the connections between nodes (e.g., from user input).
        Returns:
            The root of the created binary tree (or null if the ArrayList is empty).
        """
        if (dataList.isEmpty()) {
            return null;
        }
        ArrayList<Node> nodes = new ArrayList<>();
        for (int data : dataList) {
            if (data != -1) {
                nodes.add(new Node(data));
            } else {
                nodes.add(null);
            }
        }
        // Example logic to connect nodes (you'll need to adapt this):
        // Assuming dataList represents a level-order traversal, 
        // and you are provided with parent-child relationships separately. 
        int n = nodes.size();
        for (int i = 0; i < n; ++i) {
            if (nodes.get(i) != null) {
                int leftChildIndex = 2 * i + 1;
                int rightChildIndex = 2 * i + 2;
                if (leftChildIndex < n) {
                    nodes.get(i).left = nodes.get(leftChildIndex);
                }
                if (rightChildIndex < n) {
                    nodes.get(i).right = nodes.get(rightChildIndex);
                }
            }
        }
        return nodes.get(0); // Return the root
    }
    // (Optional) Function to print the tree in-order (for verification)
    public static void inorderTraversal(Node node) {
        if (node != null) {
            inorderTraversal(node.left);
            System.out.print(node.data + " ");
            inorderTraversal(node.right);
        }
    }
    public static void main(String[] args) {
        ArrayList<Integer> data = new ArrayList<>();
        data.add(1);
        data.add(2);
        data.add(3);
        data.add(4);
        data.add(-1);
        data.add(5);
        data.add(-1);
        data.add(-1);
        data.add(-1);
        data.add(6);
        data.add(7);
        Node root = createLinkedTree(data);
        inorderTraversal(root); // Output will depend on how you connect nodes
        System.out.println();
    }
}

#include <stdio.h>
#include <stdlib.h>
// Node structure for the binary tree
struct Node {
    int data;
    struct Node *left, *right;
};
// Function to create a new node
struct Node* newNode(int data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = node->right = NULL;
    return node;
}
// Function to create a binary tree from an array with linked representation
struct Node* createLinkedTree(int arr[], int size) {
    """
    Creates a binary tree using a linked representation from an array.
    Args:
        arr: An array of values where:
                - -1 represents an empty node.
                - The array order does not strictly imply tree structure.
                - You will likely need additional information to determine
                  the connections between nodes (e.g., from user input).
    Returns:
        The root of the created binary tree (or NULL if the array is empty).
    """
    if (size == 0) {
        return NULL;
    }
    struct Node** nodes = (struct Node**)malloc(size * sizeof(struct Node*)); 
    for (int i = 0; i < size; i++) {
        if (arr[i] != -1) {
            nodes[i] = newNode(arr[i]);
        } else {
            nodes[i] = NULL;
        }
    }
    // Example logic to connect nodes (you'll need to adapt this):
    // Assuming arr represents a level-order traversal, and you have
    // additional information to determine parent-child relationships.
    for (int i = 0; i < size; i++) {
        if (nodes[i] != NULL) {
            int leftChildIndex = 2 * i + 1;
            int rightChildIndex = 2 * i + 2;
            if (leftChildIndex < size) {
                nodes[i]->left = nodes[leftChildIndex];
            }
            if (rightChildIndex < size) {
                nodes[i]->right = nodes[rightChildIndex];
            }
        }
    }
    struct Node* root = nodes[0]; 
    free(nodes); // Free the temporary nodes array
    return root; 
}
// Function to print the tree in-order (for verification)
void inorderTraversal(struct Node* node) {
    if (node != NULL) {
        inorderTraversal(node->left);
        printf("%d ", node->data);
        inorderTraversal(node->right);
    }
}
int main() {
    int data[] = {1, 2, 3, 4, -1, 5, -1, -1, -1, 6, 7};
    int size = sizeof(data) / sizeof(data[0]);
    struct Node* root = createLinkedTree(data, size);
    printf("Inorder Traversal: ");
    inorderTraversal(root);
    printf("\n");
    // Remember to deallocate the dynamically allocated tree nodes
    // (not shown here for brevity, but crucial to avoid memory leaks)
    return 0;
}

Output:

4 2 1 5 3

BINARY TREE TRAVERSING

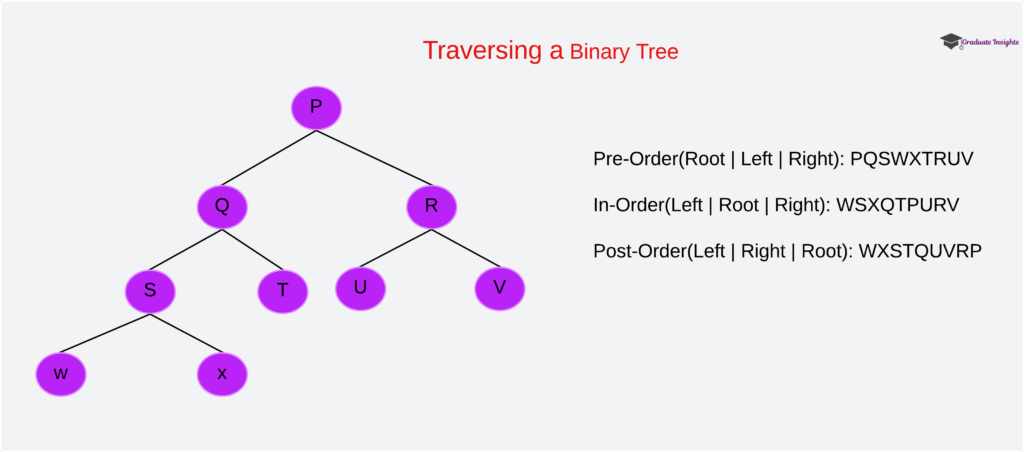
1. Processing a tree so that every node is visited exactly once is known as traversing the tree. One can navigate a binary tree in several ways. 
2. The most typical tree traversals consist of
   • Pre-Order
   • In-Order
   • Post-Order

Pre-Order(Root | Left | right):

• Firstly, visit the root node.
• Then, visit the left sub-tree of the root node.
• Finally, visit the right sub-tree of the root node. 

In-Order(Left | Root | Right):

• First, visit the left sub-tree of the root node.
• Then, visit the parent node of the left child.
• Finally, visit the parent right sub-tree.

Post-Order(Left | Right | Root):

• First, visit the left sub-tree of the root node.
• Then, visit the right sub-tree of the root node. 
• Finally, visit the root node.

Program implementation of the binary tree traversal

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
def inorder_traversal(root):
    """
    Performs an in-order traversal of the binary tree.
    In-order: Left -> Root -> Right
    """
    if root:
        inorder_traversal(root.left)  # Traverse the left subtree
        print(root.data, end=" ")    # Visit (print) the root node
        inorder_traversal(root.right) # Traverse the right subtree
def preorder_traversal(root):
    """
    Performs a pre-order traversal of the binary tree.
    Pre-order: Root -> Left -> Right
    """
    if root:
        print(root.data, end=" ")    # Visit (print) the root node
        preorder_traversal(root.left)  # Traverse the left subtree
        preorder_traversal(root.right) # Traverse the right subtree
def postorder_traversal(root):
    """
    Performs a post-order traversal of the binary tree.
    Post-order: Left -> Right -> Root
    """
    if root:
        postorder_traversal(root.left)  # Traverse the left subtree
        postorder_traversal(root.right) # Traverse the right subtree
        print(root.data, end=" ")    # Visit (print) the root node
# Example usage:
# Constructing a sample binary tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("In-order traversal: ", end="")
inorder_traversal(root)  # Output: 4 2 5 1 3 
print()
print("Pre-order traversal: ", end="")
preorder_traversal(root)  # Output: 1 2 4 5 3 
print()
print("Post-order traversal: ", end="")
postorder_traversal(root)  # Output: 4 5 2 3 1 
print()

#include <iostream>
using namespace std;
struct Node {
    int data;
    Node *left, *right;
    Node(int data) : data(data), left(nullptr), right(nullptr) {}
};
void inorderTraversal(Node* root) {
    """
    Performs an in-order traversal of the binary tree.
    In-order: Left -> Root -> Right
    """
    if (root != nullptr) {
        inorderTraversal(root->left);   // Traverse the left subtree
        cout << root->data << " ";  // Visit (print) the root node
        inorderTraversal(root->right);  // Traverse the right subtree
    }
}
void preorderTraversal(Node* root) {
    """
    Performs a pre-order traversal of the binary tree.
    Pre-order: Root -> Left -> Right
    """
    if (root != nullptr) {
        cout << root->data << " ";  // Visit (print) the root node
        preorderTraversal(root->left);   // Traverse the left subtree
        preorderTraversal(root->right);  // Traverse the right subtree
    }
}
void postorderTraversal(Node* root) {
    """
    Performs a post-order traversal of the binary tree.
    Post-order: Left -> Right -> Root
    """
    if (root != nullptr) {
        postorderTraversal(root->left);   // Traverse the left subtree
        postorderTraversal(root->right);  // Traverse the right subtree
        cout << root->data << " ";  // Visit (print) the root node
    }
}
int main() {
    // Constructing a sample binary tree
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    cout << "In-order traversal: ";
    inorderTraversal(root);  // Output: 4 2 5 1 3
    cout << endl;
    cout << "Pre-order traversal: ";
    preorderTraversal(root); // Output: 1 2 4 5 3
    cout << endl;
    cout << "Post-order traversal: ";
    postorderTraversal(root); // Output: 4 5 2 3 1 
    cout << endl;
    // Deallocate memory (Important to prevent memory leaks!)
    // (Implementation omitted for brevity, but you should 
    //  traverse the tree and delete each node). 
    return 0;
}

class Node {
    int data;
    Node left, right;
    Node(int data) {
        this.data = data;
        left = null;
        right = null;
    }
}
public class BinaryTreeTraversal {
    public static void inorderTraversal(Node root) {
        """
        Performs an in-order traversal of the binary tree.
        In-order: Left -> Root -> Right
        """
        if (root != null) {
            inorderTraversal(root.left);   // Traverse the left subtree
            System.out.print(root.data + " "); // Visit (print) the root node
            inorderTraversal(root.right);  // Traverse the right subtree
        }
    }
    public static void preorderTraversal(Node root) {
        """
        Performs a pre-order traversal of the binary tree.
        Pre-order: Root -> Left -> Right
        """
        if (root != null) {
            System.out.print(root.data + " "); // Visit (print) the root node
            preorderTraversal(root.left);   // Traverse the left subtree
            preorderTraversal(root.right);  // Traverse the right subtree
        }
    }
    public static void postorderTraversal(Node root) {
        """
        Performs a post-order traversal of the binary tree.
        Post-order: Left -> Right -> Root
        """
        if (root != null) {
            postorderTraversal(root.left);   // Traverse the left subtree
            postorderTraversal(root.right);  // Traverse the right subtree
            System.out.print(root.data + " "); // Visit (print) the root node
        }
    }
    public static void main(String[] args) {
        // Constructing a sample binary tree
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        System.out.print("In-order traversal: ");
        inorderTraversal(root);  // Output: 4 2 5 1 3
        System.out.println();
        System.out.print("Pre-order traversal: ");
        preorderTraversal(root); // Output: 1 2 4 5 3
        System.out.println();
        System.out.print("Post-order traversal: ");
        postorderTraversal(root); // Output: 4 5 2 3 1
        System.out.println();
        // No need to manually deallocate memory in Java.
        // Java's Garbage Collector handles that automatically.
    }
}

#include <stdio.h>
#include <stdlib.h>
// Node structure for the binary tree
struct Node {
    int data;
    struct Node *left, *right;
};
// Function to create a new node
struct Node* newNode(int data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = node->right = NULL;
    return node;
}
// Function for in-order traversal (Left -> Root -> Right)
void inorderTraversal(struct Node* root) {
    if (root != NULL) {
        inorderTraversal(root->left);   // Traverse the left subtree
        printf("%d ", root->data);     // Visit (print) the root node
        inorderTraversal(root->right);  // Traverse the right subtree
    }
}
// Function for pre-order traversal (Root -> Left -> Right)
void preorderTraversal(struct Node* root) {
    if (root != NULL) {
        printf("%d ", root->data);     // Visit (print) the root node
        preorderTraversal(root->left);   // Traverse the left subtree
        preorderTraversal(root->right);  // Traverse the right subtree
    }
}
// Function for post-order traversal (Left -> Right -> Root)
void postorderTraversal(struct Node* root) {
    if (root != NULL) {
        postorderTraversal(root->left);   // Traverse the left subtree
        postorderTraversal(root->right);  // Traverse the right subtree
        printf("%d ", root->data);     // Visit (print) the root node
    }
}
int main() {
    // Constructing a sample binary tree
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    printf("In-order traversal: ");
    inorderTraversal(root);  // Output: 4 2 5 1 3
    printf("\n");
    printf("Pre-order traversal: ");
    preorderTraversal(root); // Output: 1 2 4 5 3
    printf("\n");
    printf("Post-order traversal: ");
    postorderTraversal(root); // Output: 4 5 2 3 1
    printf("\n");
    // Important: Deallocate the dynamically allocated tree nodes
    // (Implementation for freeing the tree is omitted for brevity,
    //  but you need to traverse and free each node to prevent
    //  memory leaks.)
    return 0;
}

Output:

In-order traversal: 4 2 5 1 3 
Pre-order traversal: 1 2 4 5 3 
Post-order traversal: 4 5 2 3 1

Related FAQs:

1. What is the difference between a Binary Tree and a Binary Search Tree (BST)?

• A binary tree is a general structure, while a BST is a specific type where:
  • Left child nodes have values less than the parent.
  • Right child nodes have values greater than the parent.

2. How do you balance a Binary Tree?

• Balancing ensures the tree remains approximately equally divided:
  • AVL trees: Rotate nodes to balance.
  • Red-Black trees: Color nodes and rotate to balance.

3. What is the maximum height of a Binary Tree with n nodes?

• In the worst-case scenario, a binary tree can grow up to n.
• However, a self-balancing binary tree typically has a much shorter height of log(n), making search and insertion operations much more efficient.

4. How do you delete a node from a Binary Tree?

• Deletion involves:
  • Finding the node to delete.
  • Replacing it with its child (if any).
  • Rebalancing the tree (if necessary).

5. How do you traverse a Binary Tree?

• There are three main ways to traverse a binary tree:
  • Inorder Traversal: Left subtree, current node, right subtree.
  • Preorder Traversal: Current node, left subtree, right subtree.
  • Postorder Traversal: Left subtree, right subtree, current node.

6. What are the types of Binary Trees?

• There are several types of binary trees, including:
  • Full Binary Tree: Every node has two children.
  • Empty Binary Tree: No nodes.
  • Complete Binary Tree: All levels are filled except possibly the last.
  • Balanced Binary Tree: The height of left and right subtrees differs by at most one.