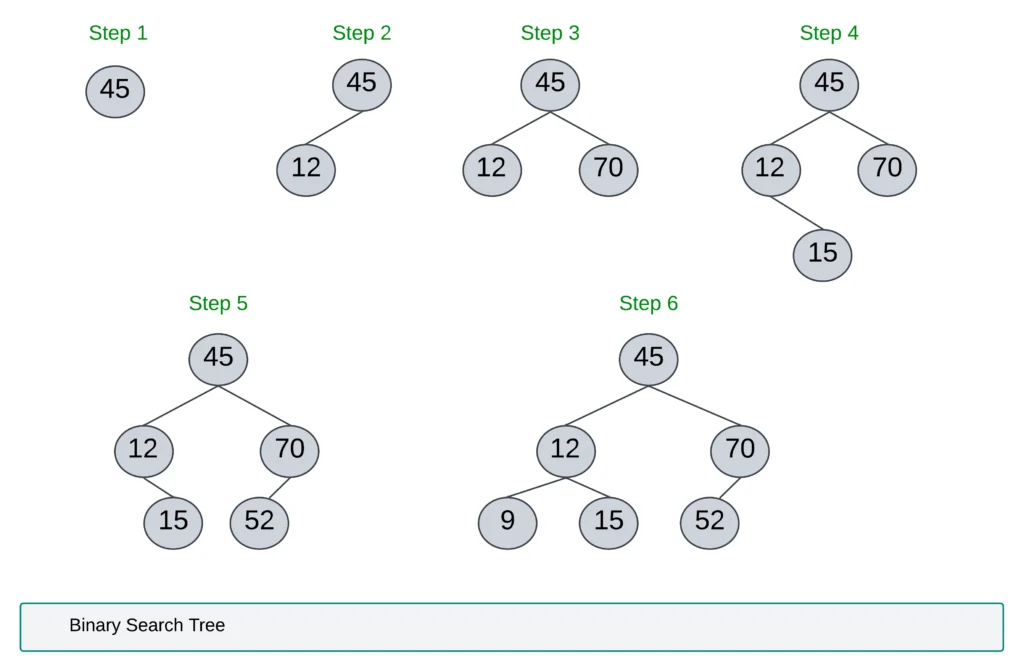
A binary search tree is a binary tree that may be empty. If it is not empty then it should satisfy the following properties:
- Every node in the tree should have a unique value.
- All elements in the left subtree are guaranteed to be less than the root node’s value.
- Every node in the right subtree exceeds the root node’s value.
- The left and right sub-trees should also be a binary search tree.
Binary search trees enable key operations including search, insertion, deletion, and traversal. We can perform all these operations very fast.
Table of Contents
Insertion in BST:
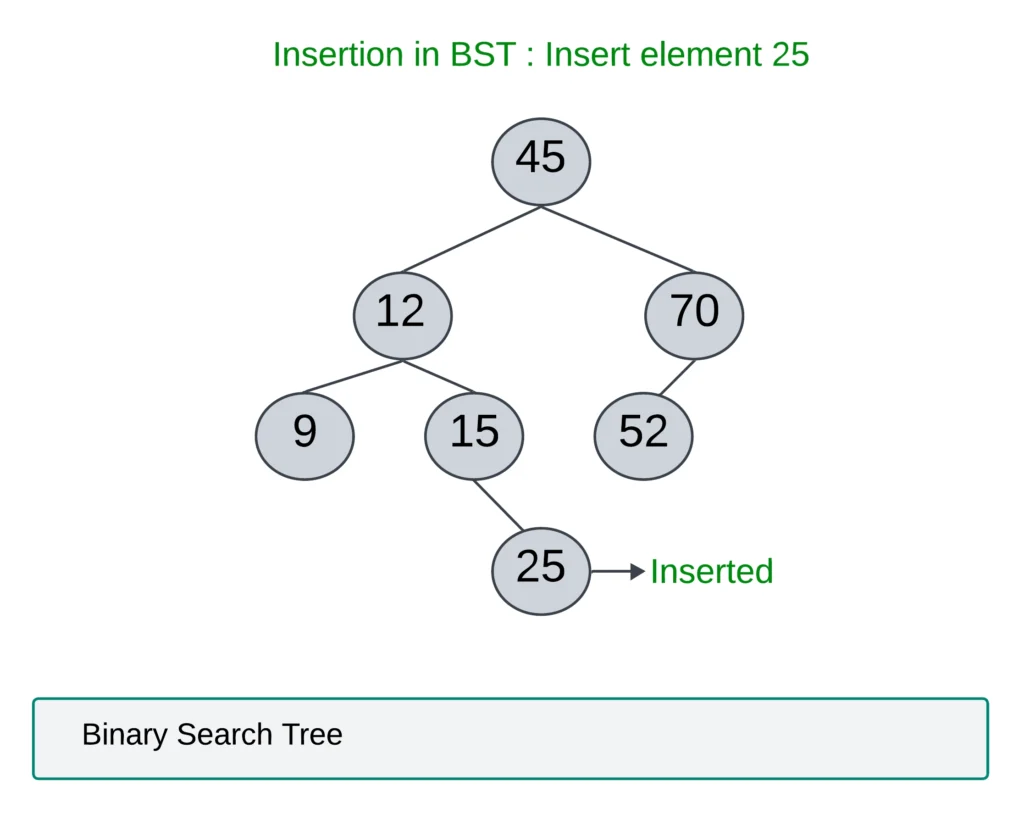
- The insertion operation on a binary search tree is straightforward. It is one more step than the search operation.
- Before inserting a new node, we must determine its appropriate position within the tree structure. The new value to be inserted must be compared against the root node’s value.
- If the value is less than the root node, traverse to the left subtree; otherwise, traverse to the right subtree.
Implementation for the above insertion in BST
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def insert(root, data):
"""
Inserts a new node with the given data into the BST.
Args:
root: The root node of the BST (or None for an empty tree).
data: The data to insert into the BST.
Returns:
The root node of the BST (possibly updated if the tree was empty).
"""
# If the tree is empty, create a new node as the root
if root is None:
return Node(data)
# Otherwise, recursively traverse the tree to find the insertion point
if data < root.data:
root.left = insert(root.left, data) # Insert in the left subtree
else:
root.right = insert(root.right, data) # Insert in the right subtree
# Return the (unchanged) root node
return root
# Example usage:
root = None # Start with an empty BST
root = insert(root, 50)
root = insert(root, 30)
root = insert(root, 20)
root = insert(root, 40)
root = insert(root, 70)
root = insert(root, 60)
root = insert(root, 80)
# (Optional) Function to print the tree in-order (for verification)
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
print(node.data, end=" ")
inorder_traversal(node.right)
print("In-order traversal (sorted order): ", end="")
inorder_traversal(root) # Output: 20 30 40 50 60 70 80
print()#include <iostream>
using namespace std;
struct Node {
int data;
Node *left, *right;
Node(int data) : data(data), left(nullptr), right(nullptr) {}
};
Node* insert(Node* root, int data) {
"""
Inserts a new node with the given data into the BST.
Args:
root: The root node of the BST (or nullptr for an empty tree).
data: The data to insert into the BST.
Returns:
The root node of the BST (possibly updated if the tree was empty).
"""
// If the tree is empty, create a new node as the root
if (root == nullptr) {
return new Node(data);
}
// Otherwise, recursively traverse the tree to find the insertion point
if (data < root->data) {
root->left = insert(root->left, data); // Insert in the left subtree
} else {
root->right = insert(root->right, data); // Insert in the right subtree
}
// Return the (unchanged) root node
return root;
}
// (Optional) Function to print the tree in-order (for verification)
void inorderTraversal(Node* node) {
if (node != nullptr) {
inorderTraversal(node->left);
cout << node->data << " ";
inorderTraversal(node->right);
}
}
int main() {
Node* root = nullptr; // Start with an empty BST
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
cout << "In-order traversal (sorted order): ";
inorderTraversal(root); // Output: 20 30 40 50 60 70 80
cout << endl;
// Important: Deallocate the dynamically allocated tree nodes
// (Implementation for freeing the tree is omitted for brevity,
// but you need to traverse and free each node to prevent
// memory leaks.)
return 0;
}class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
left = null;
right = null;
}
}
public class BSTInsertion {
public static Node insert(Node root, int data) {
"""
Inserts a new node with the given data into the BST.
Args:
root: The root node of the BST (or null for an empty tree).
data: The data to insert into the BST.
Returns:
The root node of the BST (possibly updated if the tree was empty).
"""
// If the tree is empty, create a new node as the root
if (root == null) {
return new Node(data);
}
// Otherwise, recursively traverse the tree to find the insertion point
if (data < root.data) {
root.left = insert(root.left, data); // Insert in the left subtree
} else {
root.right = insert(root.right, data); // Insert in the right subtree
}
// Return the (unchanged) root node
return root;
}
// (Optional) Function to print the tree in-order (for verification)
public static void inorderTraversal(Node node) {
if (node != null) {
inorderTraversal(node.left);
System.out.print(node.data + " ");
inorderTraversal(node.right);
}
}
public static void main(String[] args) {
Node root = null; // Start with an empty BST
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
System.out.print("In-order traversal (sorted order): ");
inorderTraversal(root); // Output: 20 30 40 50 60 70 80
System.out.println();
// No need to manually deallocate memory in Java.
// Java's Garbage Collector handles that automatically.
}
}#include <stdio.h>
#include <stdlib.h>
// Node structure for the binary search tree
struct Node {
int data;
struct Node *left, *right;
};
// Function to create a new node
struct Node* newNode(int data) {
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
// Function to insert a new node in a BST
struct Node* insert(struct Node* node, int data) {
"""
Inserts a new node with the given data into the BST.
Args:
node: The root node of the BST (or NULL for an empty tree).
data: The data to insert into the BST.
Returns:
The root node of the BST (possibly updated if the tree was empty).
"""
// If the tree is empty, return a new node
if (node == NULL) {
return newNode(data);
}
// Otherwise, recur down the tree
if (data < node->data) {
node->left = insert(node->left, data);
} else { // data >= node->data (allow duplicates to be inserted to right)
node->right = insert(node->right, data);
}
// Return the (unchanged) node pointer
return node;
}
// Function to print the tree in-order (for verification)
void inorderTraversal(struct Node* node) {
if (node != NULL) {
inorderTraversal(node->left);
printf("%d ", node->data);
inorderTraversal(node->right);
}
}
int main() {
struct Node *root = NULL; // Start with an empty BST
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("In-order traversal (sorted order): ");
inorderTraversal(root); // Output: 20 30 40 50 60 70 80
printf("\n");
// Important: Deallocate the dynamically allocated tree nodes
// (Implementation for freeing the tree is omitted for brevity,
// but you need to traverse and free each node to prevent
// memory leaks.)
return 0;
}Output:
In-order traversal (sorted order): 20 30 40 50 60 70 80 Deletion in BST:
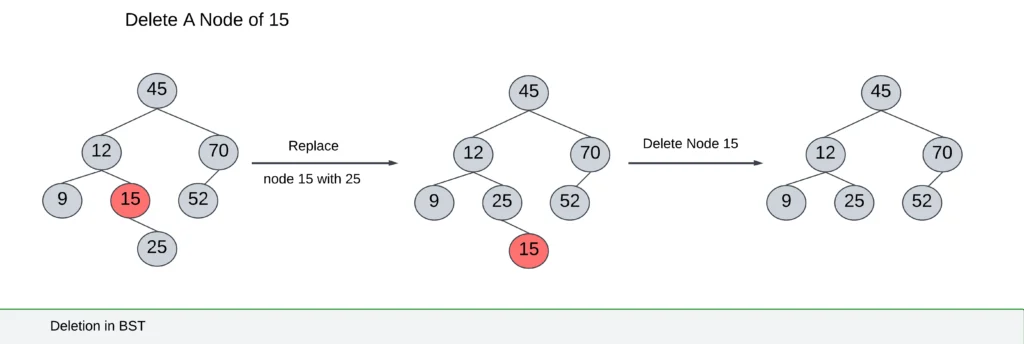
To perform the deletion operation first we have to perform the search operation. The deletion of the node depends upon the number of children. There are three possible cases.
Case-1: If the node is a leaf node, simply delete it and set its parent’s pointer to NULL.
Case-2: If a node has only one child, replace the parent node’s pointer to the node with a pointer to the node’s only child.
Case-3: If the node has two children, then we find the in-order traversal of the tree. Take the successor node of the in order and make it the parent node.
Implementation for the above Deletion in BST
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def insert(root, data):
"""
Inserts a new node with the given data into the BST.
"""
if root is None:
return Node(data)
if data < root.data:
root.left = insert(root.left, data)
else:
root.right = insert(root.right, data)
return root
def inorder_traversal(root):
"""
Performs an in-order traversal of the BST.
"""
if root:
inorder_traversal(root.left)
print(root.data, end=" ")
inorder_traversal(root.right)
def find_min(node):
"""
Finds the node with the minimum value in a subtree.
"""
current = node
while current.left is not None:
current = current.left
return current
def delete(root, data):
"""
Deletes a node with the given data from the BST.
Args:
root: The root of the BST.
data: The data to delete.
Returns:
The root of the BST (possibly updated after deletion).
"""
if root is None:
return root
if data < root.data:
root.left = delete(root.left, data)
elif data > root.data:
root.right = delete(root.right, data)
else:
# Node with only one child or no child
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
# Node with two children: Get the inorder successor (smallest in the right subtree)
temp = find_min(root.right)
# Copy the inorder successor's data to this node
root.data = temp.data
# Delete the inorder successor
root.right = delete(root.right, temp.data)
return root
# Example usage:
root = None
root = insert(root, 50)
root = insert(root, 30)
root = insert(root, 20)
root = insert(root, 40)
root = insert(root, 70)
root = insert(root, 60)
root = insert(root, 80)
print("Original tree: ", end="")
inorder_traversal(root)
print()
root = delete(root, 20)
print("After deleting 20: ", end="")
inorder_traversal(root)
print()
root = delete(root, 30)
print("After deleting 30: ", end="")
inorder_traversal(root)
print()
root = delete(root, 50)
print("After deleting 50: ", end="")
inorder_traversal(root)
print()#include <iostream>
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
Node(int data) : data(data), left(nullptr), right(nullptr) {}
};
Node* insert(Node* root, int data) {
"""
Inserts a new node with the given data into the BST.
"""
if (root == nullptr) {
return new Node(data);
}
if (data < root->data) {
root->left = insert(root->left, data);
} else {
root->right = insert(root->right, data);
}
return root;
}
void inorderTraversal(Node* root) {
"""
Performs an in-order traversal of the BST.
"""
if (root != nullptr) {
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
}
Node* findMin(Node* node) {
"""
Finds the node with the minimum value in a subtree.
"""
while (node->left != nullptr) {
node = node->left;
}
return node;
}
Node* deleteNode(Node* root, int data) {
"""
Deletes a node with the given data from the BST.
Args:
root: The root of the BST.
data: The data to delete.
Returns:
The root of the BST (possibly updated after deletion).
"""
if (root == nullptr) {
return root;
}
if (data < root->data) {
root->left = deleteNode(root->left, data);
} else if (data > root->data) {
root->right = deleteNode(root->right, data);
} else {
// Node with only one child or no child
if (root->left == nullptr) {
Node* temp = root->right;
delete root;
return temp;
} else if (root->right == nullptr) {
Node* temp = root->left;
delete root;
return temp;
}
// Node with two children: Get the inorder successor (smallest in the right subtree)
Node* temp = findMin(root->right);
// Copy the inorder successor's data to this node
root->data = temp->data;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->data);
}
return root;
}
int main() {
Node* root = nullptr;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
cout << "Original tree: ";
inorderTraversal(root);
cout << endl;
root = deleteNode(root, 20);
cout << "After deleting 20: ";
inorderTraversal(root);
cout << endl;
root = deleteNode(root, 30);
cout << "After deleting 30: ";
inorderTraversal(root);
cout << endl;
root = deleteNode(root, 50);
cout << "After deleting 50: ";
inorderTraversal(root);
cout << endl;
// Important: Deallocate the dynamically allocated tree nodes
// (Implementation for freeing the tree is omitted for brevity,
// but you need to traverse and free each node to prevent
// memory leaks.)
return 0;
}class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
left = null;
right = null;
}
}
public class BSTDeletion {
public static Node insert(Node root, int data) {
"""
Inserts a new node with the given data into the BST.
"""
if (root == null) {
return new Node(data);
}
if (data < root.data) {
root.left = insert(root.left, data);
} else {
root.right = insert(root.right, data);
}
return root;
}
public static void inorderTraversal(Node root) {
"""
Performs an in-order traversal of the BST.
"""
if (root != null) {
inorderTraversal(root.left);
System.out.print(root.data + " ");
inorderTraversal(root.right);
}
}
public static Node findMin(Node node) {
"""
Finds the node with the minimum value in a subtree.
"""
while (node.left != null) {
node = node.left;
}
return node;
}
public static Node deleteNode(Node root, int data) {
"""
Deletes a node with the given data from the BST.
Args:
root: The root of the BST.
data: The data to delete.
Returns:
The root of the BST (possibly updated after deletion).
"""
if (root == null) {
return root;
}
if (data < root.data) {
root.left = deleteNode(root.left, data);
} else if (data > root.data) {
root.right = deleteNode(root.right, data);
} else {
// Node with only one child or no child
if (root.left == null) {
Node temp = root.right;
root = null; // Important: Release the reference to the node being deleted
return temp;
} else if (root.right == null) {
Node temp = root.left;
root = null; // Important: Release the reference to the node being deleted
return temp;
}
// Node with two children: Get the inorder successor (smallest in the right subtree)
Node temp = findMin(root.right);
// Copy the inorder successor's data to this node
root.data = temp.data;
// Delete the inorder successor
root.right = deleteNode(root.right, temp.data);
}
return root;
}
public static void main(String[] args) {
Node root = null;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
System.out.print("Original tree: ");
inorderTraversal(root);
System.out.println();
root = deleteNode(root, 20);
System.out.print("After deleting 20: ");
inorderTraversal(root);
System.out.println();
root = deleteNode(root, 30);
System.out.print("After deleting 30: ");
inorderTraversal(root);
System.out.println();
root = deleteNode(root, 50);
System.out.print("After deleting 50: ");
inorderTraversal(root);
System.out.println();
// No need for manual memory deallocation in Java due to garbage collection
}
}#include <stdio.h>
#include <stdlib.h>
// Node structure for the Binary Search Tree
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// Function to create a new node
struct Node* newNode(int data) {
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
// Function to insert a new node into the BST
struct Node* insert(struct Node* node, int data) {
"""
Inserts a new node with the given data into the BST.
"""
if (node == NULL) {
return newNode(data);
}
if (data < node->data) {
node->left = insert(node->left, data);
} else {
node->right = insert(node->right, data);
}
return node;
}
// Function for in-order traversal of the BST
void inorderTraversal(struct Node* node) {
if (node != NULL) {
inorderTraversal(node->left);
printf("%d ", node->data);
inorderTraversal(node->right);
}
}
// Function to find the node with the minimum value in a subtree
struct Node* findMin(struct Node* node) {
while (node->left != NULL) {
node = node->left;
}
return node;
}
// Function to delete a node from the BST
struct Node* deleteNode(struct Node* root, int data) {
"""
Deletes a node with the given data from the BST.
Args:
root: The root of the BST.
data: The data to delete.
Returns:
The root of the BST (possibly updated after deletion).
"""
if (root == NULL) {
return root;
}
if (data < root->data) {
root->left = deleteNode(root->left, data);
} else if (data > root->data) {
root->right = deleteNode(root->right, data);
} else {
// Node with only one child or no child
if (root->left == NULL) {
struct Node* temp = root->right;
free(root); // Free the node being deleted
return temp;
} else if (root->right == NULL) {
struct Node* temp = root->left;
free(root); // Free the node being deleted
return temp;
}
// Node with two children: Get the inorder successor
struct Node* temp = findMin(root->right);
// Copy the inorder successor's data to this node
root->data = temp->data;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->data);
}
return root;
}
int main() {
struct Node* root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Original tree: ");
inorderTraversal(root);
printf("\n");
root = deleteNode(root, 20);
printf("After deleting 20: ");
inorderTraversal(root);
printf("\n");
root = deleteNode(root, 30);
printf("After deleting 30: ");
inorderTraversal(root);
printf("\n");
root = deleteNode(root, 50);
printf("After deleting 50: ");
inorderTraversal(root);
printf("\n");
// Important: Deallocate the dynamically allocated tree nodes
// (Implementation for freeing the tree is omitted for brevity,
// but you need to traverse and free each node to prevent
// memory leaks.)
return 0;
}Output:
Original tree: 20 30 40 50 60 70 80
After deleting 20: 30 40 50 60 70 80
After deleting 30: 40 50 60 70 80
After deleting 50: 40 60 70 80Searching in BST:
- This process begins with the root node. The search element is compared with the root node. If it is present then it returns the root node value.
- If the search element is less than the root, the search proceeds to the left subtree.
- If the search element exceeds the root, the search continues in the right subtree.
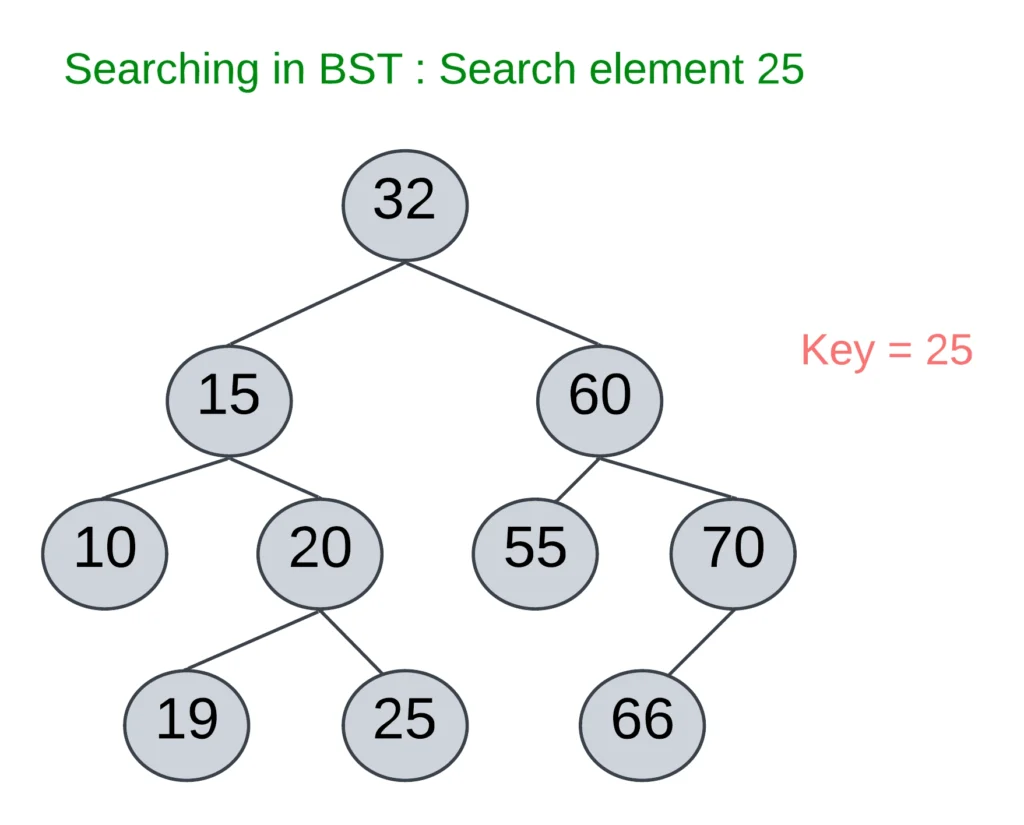
- In the above BST search element “key=25” check the root value first,
- The root element is 35 which is less than the key element then search in the left subtree
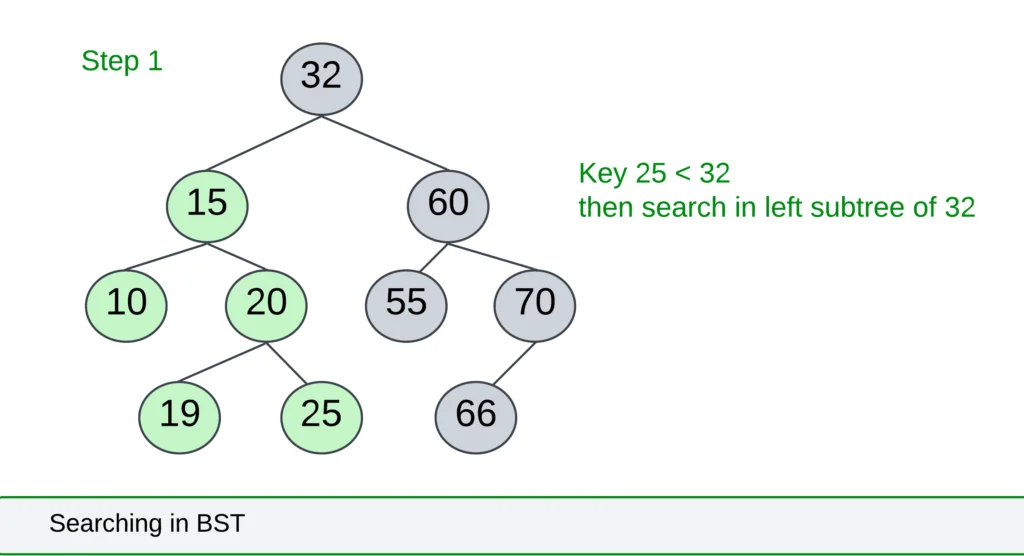
- Now, Parent node 15 which is less than the key element then moves to the right subtree of 15
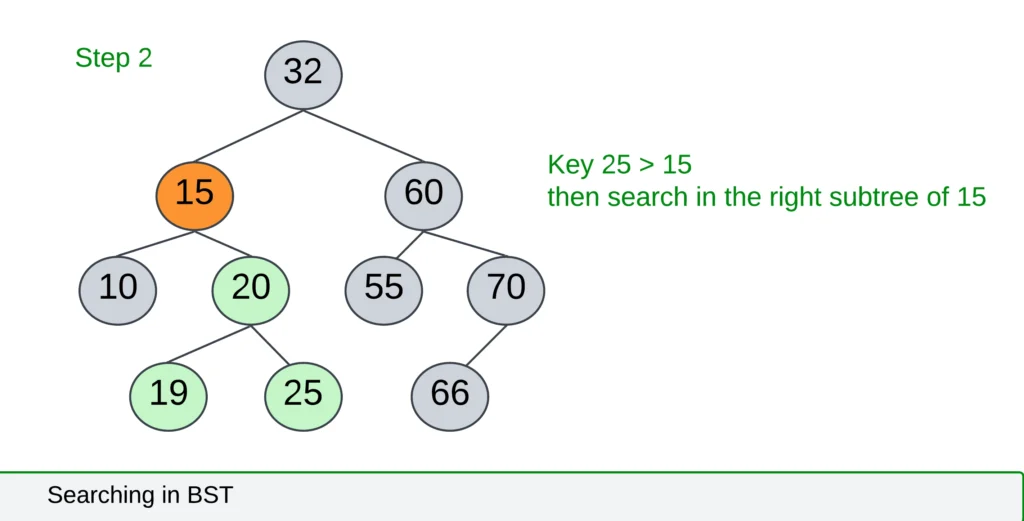
- Now, Check element 20(i.e 25 > 20) then move to the right subtree of 20
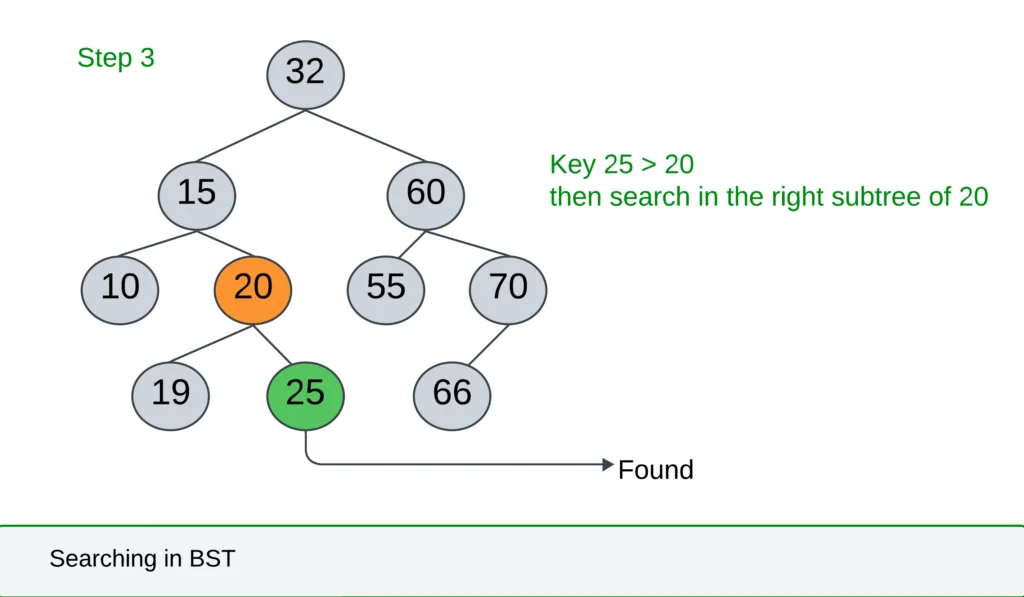
- Element 25 = 25, found the key element.
Implementation for the above Searching in BST
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def insert(root, data):
"""
Inserts a new node with the given data into the BST.
"""
if root is None:
return Node(data)
if data < root.data:
root.left = insert(root.left, data)
else:
root.right = insert(root.right, data)
return root
def search(root, data):
"""
Searches for a node with the given data in the BST.
Args:
root: The root node of the BST.
data: The data to search for.
Returns:
True if the data is found, False otherwise.
"""
if root is None:
return False # Empty tree
if root.data == data:
return True # Data found
if data < root.data:
return search(root.left, data) # Search in the left subtree
else:
return search(root.right, data) # Search in the right subtree
# Example usage:
root = None
root = insert(root, 50)
root = insert(root, 30)
root = insert(root, 20)
root = insert(root, 40)
root = insert(root, 70)
root = insert(root, 60)
root = insert(root, 80)
print(f"Is 40 present? {search(root, 40)}") # Output: True
print(f"Is 100 present? {search(root, 100)}") # Output: False#include <iostream>
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
Node(int data) : data(data), left(nullptr), right(nullptr) {}
};
Node* insert(Node* root, int data) {
"""
Inserts a new node with the given data into the BST.
"""
if (root == nullptr) {
return new Node(data);
}
if (data < root->data) {
root->left = insert(root->left, data);
} else {
root->right = insert(root->right, data);
}
return root;
}
bool search(Node* root, int data) {
"""
Searches for a node with the given data in the BST.
Args:
root: The root node of the BST.
data: The data to search for.
Returns:
True if the data is found, False otherwise.
"""
if (root == nullptr) {
return false; // Empty tree
}
if (root->data == data) {
return true; // Data found
}
if (data < root->data) {
return search(root->left, data); // Search in the left subtree
} else {
return search(root->right, data); // Search in the right subtree
}
}
int main() {
Node* root = nullptr;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
cout << "Is 40 present? " << search(root, 40) << endl; // Output: True
cout << "Is 100 present? " << search(root, 100) << endl; // Output: False
// Important: Deallocate the dynamically allocated tree nodes
// (Implementation for freeing the tree is omitted for brevity,
// but you need to traverse and free each node to prevent
// memory leaks.)
return 0;
}class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
left = null;
right = null;
}
}
public class BSTSearch {
public static Node insert(Node root, int data) {
"""
Inserts a new node with the given data into the BST.
"""
if (root == null) {
return new Node(data);
}
if (data < root.data) {
root.left = insert(root.left, data);
} else {
root.right = insert(root.right, data);
}
return root;
}
public static boolean search(Node root, int data) {
"""
Searches for a node with the given data in the BST.
Args:
root: The root node of the BST.
data: The data to search for.
Returns:
True if the data is found, False otherwise.
"""
if (root == null) {
return false; // Empty tree
}
if (root.data == data) {
return true; // Data found
}
if (data < root.data) {
return search(root.left, data); // Search in the left subtree
} else {
return search(root.right, data); // Search in the right subtree
}
}
public static void main(String[] args) {
Node root = null;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
System.out.println("Is 40 present? " + search(root, 40)); // Output: True
System.out.println("Is 100 present? " + search(root, 100)); // Output: False
}
}#include <stdio.h>
#include <stdlib.h>
// Node structure for the Binary Search Tree
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// Function to create a new node
struct Node* newNode(int data) {
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
// Function to insert a new node into the BST
struct Node* insert(struct Node* node, int data) {
"""
Inserts a new node with the given data into the BST.
"""
if (node == NULL) {
return newNode(data);
}
if (data < node->data) {
node->left = insert(node->left, data);
} else {
node->right = insert(node->right, data);
}
return node;
}
// Function to search for a node in the BST
bool search(struct Node* root, int data) {
"""
Searches for a node with the given data in the BST.
Args:
root: The root node of the BST.
data: The data to search for.
Returns:
True if the data is found, False otherwise.
"""
if (root == NULL) {
return false; // Empty tree
}
if (root->data == data) {
return true; // Data found
}
if (data < root->data) {
return search(root->left, data); // Search in the left subtree
} else {
return search(root->right, data); // Search in the right subtree
}
}
int main() {
struct Node* root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Is 40 present? %d\n", search(root, 40)); // Output: True
printf("Is 100 present? %d\n", search(root, 100)); // Output: False
// Important: Deallocate the dynamically allocated tree nodes
// (Implementation for freeing the tree is omitted for brevity,
// but you need to traverse and free each node to prevent
// memory leaks.)
return 0;
}Output:
Is 40 present? True
Is 100 present? FalseTime and Space Complexity of BST Operations
Here’s a breakdown of the time and space complexities associated with common operations on a Binary Search Tree (BST), presented in a table format:
| Operation | Average Case Time Complexity | Worst Case Time Complexity | Space Complexity |
| Insertion | O(log n) | O(n) | O(log n) |
| Deletion | O(log n) | O(n) | O(log n) |
| Search | O(log n) | O(n) | O(log n) |
| Min/Max | O(log n) | O(n) | O(log n) |
| Inorder Traversal | O(n) | O(n) | O(1) |
| Preorder Traversal | O(n) | O(n) | O(1) |
| Postorder Traversal | O(n) | O(n) | O(1) |
Advantages of BST
Here are 5 key advantages of Binary Search Trees (BSTs) in DSA:
- Efficient Searching: BSTs offer fast search operations with a time complexity of O(log n) in balanced trees, significantly outperforming linear search in arrays or linked lists for large datasets.
- Inherent Ordering: Data within a BST is always stored in a sorted order, eliminating the need for additional sorting algorithms when retrieving elements in ascending or descending order.
- Dynamic Insertion and Deletion: BSTs support efficient insertion and deletion operations, typically with logarithmic time complexity, making them suitable for dynamic datasets that change frequently.
- Foundation for Advanced Structures: BSTs are the building blocks for more advanced data structures like AVL trees, red-black trees, and heaps, expanding their use in various algorithms.
- Efficient Range Queries: Binary Search Trees (BSTs) facilitate fast and efficient data retrieval within specified ranges, proving highly beneficial for database management and query optimization.
Disadvantages of BST
Here are the disadvantages of Binary Search Trees (BSTs) broken down by sentence:
- Worst-Case Time Complexity: While generally efficient, BSTs can suffer from linear time complexity (O(n)) in their worst-case scenario.
- Not Inherently Balanced: BSTs do not inherently maintain balance, meaning their structure depends on the order of data insertion.
- Overhead of Maintaining Order: BSTs necessitate maintaining a specific order (left subtree < node < right subtree) for their functionality.
- Space Complexity: BSTs have a linear space complexity (O(n)), signifying that the memory required grows proportionally with the number of nodes.
- Navigating Inorder Traversal: While inorder traversal of a BST produces a sorted list of nodes, locating a specific element within this traversal necessitates visiting all preceding nodes.
Applications of BST
1. Efficient Searching and Sorting:
- Benefit: BSTs excel at searching for specific values with a tian average complexity of O(log n) significantly faster than linear search in arrays.
- Use Case: Find a student record by ID in a school database or locate a specific product in an e-commerce platform.
2. Implementing Symbol Tables:
- Benefit: BSTs efficiently store key-value pairs, forming the backbone of symbol tables used in compilers and interpreters.
- Use Case: Storing variable names (keys) and their corresponding values during program compilation for efficient lookup during runtime.
3. Auto-completion and Suggestion Systems:
- Benefit: BST variations like Trie structures efficiently store and search strings, forming the foundation of auto-completion features.
- Use Case: Suggesting search terms in search engines (like Google) or recommending words while typing in text editors and messaging apps.
4. Navigating Hierarchical Data:
- BSTs inherently represent hierarchical relationships, making them suitable for representing file systems or organizational structures.
5. Order Statistics and Range Queries:
- Benefit: BSTs can be augmented to efficiently answer order statistics queries (e.g., finding the kth smallest element) and range queries (finding values within a given range).
- Use Case: Retrieving the top 10 ranked players in a gaming leaderboard or finding products within a specific price range in an online store.
Related FAQs
1. What is a Balanced Binary Search Tree, and Why is it Important?
- A binary search tree is considered balanced if, for every node, the difference in height between its left and right subtrees is either zero or one, ensuring a relatively even distribution of nodes.
- Balancing is crucial to prevent worst-case scenarios where BST operations could degrade to O(n) time complexity.
- Techniques like AVL trees and red-black trees are used to maintain balance.
2. How Do You Insert a Node into a Binary Search Tree?
- To insert a new node, start at the root and compare the new node’s value with the current node’s.
- If smaller, move to the left subtree; if larger, move to the right subtree.
- Repeat until you find a vacant position, indicated by a leaf node with no children, where the new node can be successfully inserted.
3. How Do You Delete a Node from a Binary Search Tree?
- Deleting a node is more complex and depends on the element’s position and the number of children it has.
- In general, you either replace the node with its inorder successor (the smallest node in its right subtree) or its inorder predecessor (the largest node in its left subtree) or directly remove it if it’s a leaf node.
4. What are the differences between Inorder, Preorder, and Postorder traversal methods in a Binary Search Tree?
These are different ways to visit all nodes in a BST:
- In order: Traverse the left subtree first, followed by the current node, and finally the right subtree. This results in a sorted order of values.
- Preorder: Traverse the tree starting at the current node, then its left subtree, and ending with its right subtree.
- Postorder: Traverse the left subtree, followed by the right subtree, and finally the node.
5. How Do You Find the Minimum and Maximum Values in a Binary Search Tree?
- Minimum: Start at the root and keep moving to the left child until you reach a node with no left child. That node holds the minimum value.
- Maximum: Start at the root and keep moving to the right child until you reach a node with no right child. That node holds the maximum value.
