What is a Binary Search Algorithm?
- The binary search is a search algorithm that works more efficiently than the linear search.
- Binary search works on the principle of divide and conquer policy.
- The basis of binary search is to divide the list of elements into two halves.
- Binary search is a search algorithm designed for sorted datasets (e.g., lists, arrays).
- The search element is compared with the middle element of the list.
- If it matches then it returns the middle value of the list.
- If the search element is less than the middle element of the list, it checks only the first half of the list and neglects the second half.
- If the search element is greater than the middle element then it executes the second half by neglecting the first half.
- Again, the list of elements is divided into two halves and the search process continues as discussed above.
- Every time, a list of elements is divided into two halves and performs a search operation then it is called a binary search. The logic of binary search is
Low=0, high=n-1
Algorithm of Binary Search
Step-by-Step Binary Search Algorithm
- Initialization:
- Define the search interval’s low and high indices. Initially, low points to the first element (index 0), and high points to the last element (index n-1, where n is the number of elements).
- Determine the target value you want to find.
- Iteration:
- Repeat the following steps as long as low is less than or equal to high:
- Calculate the mid index: mid = low + (high – low) / 2 (To avoid potential overflow in some languages).
- Compare the middle element at index mid with the target value:
- If the middle element equals the target value, return the mid index as the result.
- If the middle element is smaller than the target value, update low to mid + 1 (search in the right half).
- If the middle element is larger than the target value, update high to mid-1 (search in the left half).
- Repeat the following steps as long as low is less than or equal to high:
- Termination:
- If the target value is not found after the loop terminates (i.e., low becomes greater than high), return a value indicating that the element is not present in the dataset (-1 is a common convention).
Table of Contents
Steps of Working Binary Search Algorithm with an Example
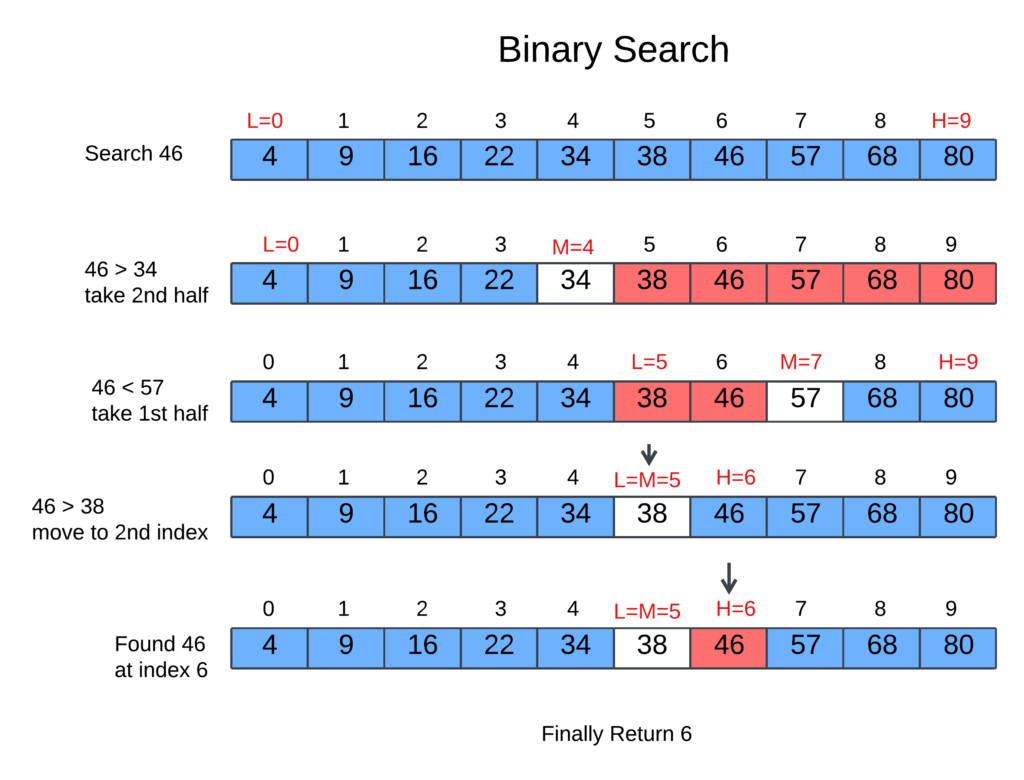
Step 1: Initialize the variables:
- low = 0 (index of the first element)
- high = 9 (index of the last element)
- target = 46 (the element to search for)
Step 2: Calculate the middle index:
- mid = (low + high) // 2 = (0 + 9) // 2 = 4
Step 3: Compare the middle element with the target:
- arr[mid] (the element at index 4) = 34
- Since 46 > 34, the target element must be in the right half of the list.
Step 4: Update the low index to mid + 1:
- low = 5
Step 5: Repeat steps 2-4 until the target element is found or the search space is empty:
- mid = (low + high) // 2 = (5 + 9) // 2 = 7
- arr[mid] (the element at index 7) = 57
- Since 46 < 57, the target element must be in the left half of the list.
Step 6: Update the high index to mid-1:
- high = 6
Step 7: Repeat steps 2-4 until the target element is found or the search space is empty:
- mid = (low + high) // 2 = (5 + 6) // 2 = 5
- arr[mid] (the element at index 5) = 46
- The target element has been found!
Step 8: Return the index of the target element:
- The target element is at index 5.
Implementing Binary Search Algorithm
- 2 ways to implement the Binary Search Algorithm
- 1. Iterative Binary Search Algorithm
- 2. Recursive Binary Search Algorithm
Iterative Binary Search Algorithm Program
def binary_search(arr, target):
"""
Performs iterative binary search on a sorted list/array.
Args:
arr: The sorted list/array to search in.
target: The value to search for.
Returns:
The index of the target element if found, otherwise -1.
"""
low = 0 # Initialize the low index (start of the search interval)
high = len(arr) - 1 # Initialize the high index (end of the search interval)
while low <= high: # Continue searching while there's a valid interval
mid = low + (high - low) // 2 # Calculate the middle index (avoid potential overflow)
if arr[mid] == target: # Check if the middle element is the target
return mid # Found the target, return its index
elif arr[mid] < target: # Target is larger, search in the right half
low = mid + 1
else: # Target is smaller, search in the left half
high = mid - 1
return -1 # Target not found in the list
# Example usage
arr = [2, 5, 8, 12, 16, 23, 38, 56, 72, 91]
target = 23
result = binary_search(arr, target)
if result != -1:
print("Target found at index:", result)
else:
print("Target not found in the list")
#include <iostream>
#include <vector>
using namespace std;
int binarySearch(const vector<int>& arr, int target) {
/*
* Performs iterative binary search on a sorted vector.
*
* Args:
* arr: The sorted vector to search in.
* target: The value to search for.
*
* Returns:
* The index of the target element if found, otherwise -1.
*/
int low = 0; // Initialize the low index (start of search interval)
int high = arr.size() - 1; // Initialize the high index (end of search interval)
while (low <= high) { // Continue searching while there's a valid interval
int mid = low + (high - low) / 2; // Calculate the middle index (avoid potential overflow)
if (arr[mid] == target) { // Check if the middle element is the target
return mid; // Found the target, return its index
} else if (arr[mid] < target) { // Target is larger, search in the right half
low = mid + 1; // Update the low index
} else { // Target is smaller, search in the left half
high = mid - 1; // Update the high index
}
}
return -1; // Target not found in the vector
}
int main() {
vector<int> arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = binarySearch(arr, target);
if (result != -1) {
cout << "Target found at index: " << result << endl;
} else {
cout << "Target not found in the vector" << endl;
}
return 0;
}
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
/*
* Performs iterative binary search on a sorted array.
*
* Args:
* arr: The sorted array to search in.
* target: The value to search for.
*
* Returns:
* The index of the target element if found, otherwise -1.
*/
int low = 0; // Initialize the low index (start of search interval)
int high = arr.length - 1; // Initialize the high index (end of search interval)
while (low <= high) { // Continue searching while there's a valid interval
int mid = low + (high - low) / 2; // Calculate the middle index (avoid potential overflow)
if (arr[mid] == target) { // Check if the middle element is the target
return mid; // Found the target, return its index
} else if (arr[mid] < target) { // Target is larger, search in the right half
low = mid + 1; // Update the low index
} else { // Target is smaller, search in the left half
high = mid - 1; // Update the high index
}
}
return -1; // Target not found in the array
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = binarySearch(arr, target);
if (result != -1) {
System.out.println("Target found at index: " + result);
} else {
System.out.println("Target not found in the array");
}
}
}
#include <stdio.h>
int binarySearch(int arr[], int size, int target) {
/*
* Performs iterative binary search on a sorted array.
*
* Args:
* arr: The sorted array to search in.
* size: The size of the array.
* target: The value to search for.
*
* Returns:
* The index of the target element if found, otherwise -1.
*/
int low = 0; // Initialize the low index (start of search interval)
int high = size - 1; // Initialize the high index (end of search interval)
while (low <= high) { // Continue searching while there's a valid interval
int mid = low + (high - low) / 2; // Calculate the middle index (avoid potential overflow)
if (arr[mid] == target) { // Check if the middle element is the target
return mid; // Found the target, return its index
} else if (arr[mid] < target) { // Target is larger, search in the right half
low = mid + 1; // Update the low index
} else { // Target is smaller, search in the left half
high = mid - 1; // Update the high index
}
}
return -1; // Target not found in the array
}
int main() {
int arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int size = sizeof(arr) / sizeof(arr[0]); // Calculate the size of the array
int target = 23;
int result = binarySearch(arr, size, target);
if (result != -1) {
printf("Target found at index: %d\n", result);
} else {
printf("Target not found in the array\n");
}
return 0;
}
Output:
Target found at index: 5Recursive Binary Search Algorithm Program
def binary_search_recursive(arr, target, low, high):
"""
Performs recursive binary search on a sorted list/array.
Args:
arr: The sorted list/array to search in.
target: The value to search for.
low: The low index (start of the current search interval).
high: The high index (end of the current search interval).
Returns:
The index of the target element if found, otherwise -1.
"""
# Base case: interval is invalid (element not found)
if low > high:
return -1
mid = low + (high - low) // 2 # Calculate the middle index
if arr[mid] == target: # Base case: target found
return mid
elif arr[mid] < target: # Target is larger, search in the right half
return binary_search_recursive(arr, target, mid + 1, high)
else: # Target is smaller, search in the left half
return binary_search_recursive(arr, target, low, mid - 1)
# Example usage
arr = [2, 5, 8, 12, 16, 23, 38, 56, 72, 91]
target = 23
result = binary_search_recursive(arr, target, 0, len(arr) - 1)
if result != -1:
print("Target found at index:", result)
else:
print("Target not found in the list")
#include <iostream>
#include <vector>
using namespace std;
int binarySearchRecursive(const vector<int>& arr, int target, int low, int high) {
/*
* Performs recursive binary search on a sorted vector.
*
* Args:
* arr: The sorted vector to search in.
* target: The value to search for.
* low: The low index (start of the current search interval).
* high: The high index (end of the current search interval).
*
* Returns:
* The index of the target element if found, otherwise -1.
*/
// Base case: interval is invalid (element not found)
if (low > high) {
return -1;
}
int mid = low + (high - low) / 2; // Calculate the middle index (avoid potential overflow)
// Base case: target found
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) { // Target is larger, search in the right half
return binarySearchRecursive(arr, target, mid + 1, high);
} else { // Target is smaller, search in the left half
return binarySearchRecursive(arr, target, low, mid - 1);
}
}
int main() {
vector<int> arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = binarySearchRecursive(arr, target, 0, arr.size() - 1);
// Initial call with low = 0 and high = last index
if (result != -1) {
cout << "Target found at index: " << result << endl;
} else {
cout << "Target not found in the vector" << endl;
}
return 0;
}
public class BinarySearchRecursive {
public static int binarySearchRecursive(int[] arr, int target, int low, int high) {
/*
* Performs recursive binary search on a sorted array.
*
* Args:
* arr: The sorted array to search in.
* target: The value to search for.
* low: The low index (start of the current search interval).
* high: The high index (end of the current search interval).
*
* Returns:
* The index of the target element if found, otherwise -1.
*/
// Base case: interval is invalid (element not found)
if (low > high) {
return -1;
}
int mid = low + (high - low) / 2; // Calculate the middle index (avoid potential overflow)
// Base case: target found
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) { // Target is larger, search in the right half
return binarySearchRecursive(arr, target, mid + 1, high);
} else { // Target is smaller, search in the left half
return binarySearchRecursive(arr, target, low, mid - 1);
}
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = binarySearchRecursive(arr, target, 0, arr.length - 1);
// Initial call with low = 0 and high = last index
if (result != -1) {
System.out.println("Target found at index: " + result);
} else {
System.out.println("Target not found in the array");
}
}
}
#include <stdio.h>
int binarySearchRecursive(int arr[], int target, int low, int high) {
/*
* Performs recursive binary search on a sorted array.
*
* Args:
* arr: The sorted array to search in.
* target: The value to search for.
* low: The low index (start of the current search interval).
* high: The high index (end of the current search interval).
*
* Returns:
* The index of the target element if found, otherwise -1.
*/
// Base case: interval is invalid (element not found)
if (low > high) {
return -1;
}
int mid = low + (high - low) / 2; // Calculate the middle index (avoid potential overflow)
// Base case: target found
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) { // Target is larger, search in the right half
return binarySearchRecursive(arr, target, mid + 1, high);
} else { // Target is smaller, search in the left half
return binarySearchRecursive(arr, target, low, mid - 1);
}
}
int main() {
int arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int size = sizeof(arr) / sizeof(arr[0]); // Calculate the size of the array
int target = 23;
int result = binarySearchRecursive(arr, target, 0, size - 1);
// Initial call with low = 0 and high = last index
if (result != -1) {
printf("Target found at index: %d\n", result);
} else {
printf("Target not found in the array\n");
}
return 0;
}
Output:
Target found at index: 5Time Complexity of Binary Search vs Linear Search Algorithms
| Time Complexity | Best Case | Worst Case | Average Case |
| Binary Search | O(1) | O(log n) | O(log n) |
| Linear Search | O(1) | O(n) | O(n) |
Explanation:
- Time Complexity:
- Best Case: O(1) – When the target element is found at the middle index in the first comparison.
- Worst Case: O(log n) – Where ‘n’ is the number of elements in the sorted array. In the worst-case scenario, the search interval is halved in each iteration until it contains only one element.
- Average Case: O(log n) – The average time complexity is also logarithmic.
- Space Complexity:
- Iterative Binary Search: O(1) – It uses a constant amount of extra space, regardless of the input size, as it only needs variables to keep track of the low, high, and mid indices.
- Recursive Binary Search: O(log n) – The recursive implementation uses space on the call stack due to recursive function calls. In the worst case, the maximum depth of recursion is log n.
Applications of Binary Search
- Software Development:
- Debugging: Quickly locate a specific line of code causing an error within a sorted log file.
- Version Control: Efficiently identify the revision where a bug was introduced in code repositories.
- Resource Optimization: Find the optimal allocation of resources in a system by narrowing down possibilities.
- Data Science and Machine Learning:
- Feature Selection: Determine the most relevant features for a model by evaluating their impact within a sorted list.
- Hyperparameter Tuning: Efficiently search for the best combination of hyperparameters to optimize model performance.
- Anomaly Detection: Identify unusual data points in a sorted dataset by comparing them against expected ranges.
- Databases and Information Retrieval:
- Searching Sorted Data: Rapidly retrieve specific records in databases or indexed files.
- Range Queries: Efficiently find all values within a specified range in a sorted dataset.
- Maintaining Sorted Lists: Inserting new elements into a sorted list while preserving order.
- Networking and Security:
- Network Routing: Quickly determine the optimal path for data packets based on sorted routing tables.
- Intrusion Detection: Identify unauthorized access attempts by comparing network traffic patterns against sorted profiles.
- Load Balancing: Distribute incoming traffic efficiently across servers by utilizing sorted load information.
- Other Applications:
- Game Development: Determine enemy positions, AI decision-making, and pathfinding in sorted game worlds.
- Numerical Analysis: Solving equations and finding roots of functions through iterative halving of intervals.
- Financial Modeling: Calculating optimal investment strategies by evaluating sorted scenarios.
Advantages of Binary Search Algorithm
- Lightning-Fast Speed: Binary search excels at speed. Thanks to its logarithmic time complexity (O(log n)), it finds your target value in very few steps, even for massive datasets. This is a major advantage over linear search (O(n)), which slows way down with large data.
- Efficiency at Its Core: Binary search cuts the search space in half with each comparison, dramatically reducing steps to find the element.
- Simplicity and Elegance: Binary search shines in its simplicity. The core idea of halving the search space is easy to understand, making it straightforward to implement.
- Versatility in Applications: Binary search has a wide range of uses beyond simple array searches, including debugging, resource optimization, database queries, and machine learning.
- Reliability and Accuracy: Binary search is deterministic, ensuring consistent and accurate results.
Disadvantages of Binary Search Algorithm
- Requires Sorted Data: Binary search works best with pre-sorted data. For unsorted data, consider hash tables or tree-based structures.
- Not Ideal for Linked Lists: Binary search is optimized for random access, making it less efficient for linked lists.
- Tricky Implementation for Beginners: Binary search can be tricky to implement correctly, especially for beginners, due to potential index calculation errors.
- Less Efficient for Small Datasets: For tiny datasets, the binary search setup might outweigh its benefits. Linear search can be simpler and faster in these cases.
- Limited to Exact Matches: Binary search only finds exact matches. Consider alternatives for range searches or approximations.
Frequently Asked Questions (FAQs) on Binary Search Algorithm
Q1. What is binary search?
Binary search is an efficient algorithm for finding a specific target value within a sorted dataset. It repeatedly divides the search interval in half, eliminating the half that doesn’t contain the target.
Q2. What are the main advantages of binary search?
- Speed: Its logarithmic time complexity (O(log n)) makes it significantly faster than linear search (O(n)) for large datasets.
- Efficiency: It dramatically reduces the number of comparisons needed to find an element.
- Simplicity: While powerful, the core concept of halving the search space is easy to grasp.
Q3. What are the disadvantages of binary search?
- Sorted Data Requirement: Binary search only works on sorted data. If data is unsorted, it must be sorted first, adding overhead.
- Implementation Challenges: Correctly implementing binary search can be tricky, especially handling edge cases like array boundaries.
Q4. When should I use binary search?
- Sorted Data: When you have a sorted array, list, or similar data structure.
- Frequent Lookups: Binary search excels when you need to perform numerous searches in the same dataset.
Q5. When should I avoid binary search?
- Unsorted Data: For unsorted data, consider using linear search (if the dataset is small) or hash tables for faster lookups.
- Linked Lists: Binary search is less efficient for linked lists due to their non-random access nature.
Q6. What are some real-world applications of binary search?
- Debugging: Finding a specific line of code in a sorted log file.
- Version Control: Identifying the code revision where a bug was introduced.
- Databases: Quickly searching for records in sorted indexes.
- Networking: Efficiently routing data packets using sorted routing tables.
Q7. Can you explain binary search with an example?
Imagine finding a word in a dictionary. You wouldn’t start from the beginning; instead, you’d open the dictionary in the middle. If the word you’re looking for comes after that page, you discard the first half. You repeat this process, halving the remaining pages until you find your word. Binary search works similarly in code, but with numerical comparisons.
Related topics:
