AVL Tree in Data Structure with example

Leave a Comment / Data Structures, Trees / By
  • AVL trees are self-balancing binary search trees known for efficient data storage and retrieval. 
  • Developed in 1962 by Adelson-Velsky and Landis, they guarantee a search, insertion, and deletion time complexity of O(log n), where ‘n’ represents the total number of nodes. 
  • The tree’s ability to maintain balance ensures that all branches remain relatively short, contributing to its overall efficiency.

What Defines an AVL Tree?

  • Building upon the foundation of a binary search tree, an AVL tree introduces a key constraint: the heights of the left and right subtrees of any node cannot differ by more than 1.
  • This difference, known as the balance factor, can be -1, 0, or +1.

Understanding Balance Factor:

A node’s balance factor (BF) is computed as follows:

BF(T) = hL – hR

Where:

  • hL: Height of the left subtree
  • hR: Height of the right subtree

This property ensures the tree remains relatively balanced, preventing scenarios where search operations could degenerate into linear time complexity, similar to searching an unsorted list.

Height of an AVL Tree:

  • The maximum height of an AVL tree is always O(log n). 
  • This logarithmic height is critical for efficient search, insertion, and deletion operations.

AVL Tree Representation:

  • AVL trees are typically represented visually, similar to binary search trees, but with the addition of the balance factor displayed within each node. 
  • This visual representation aids in understanding the tree’s structure and balance.

Operations on AVL Trees:

Insertion:

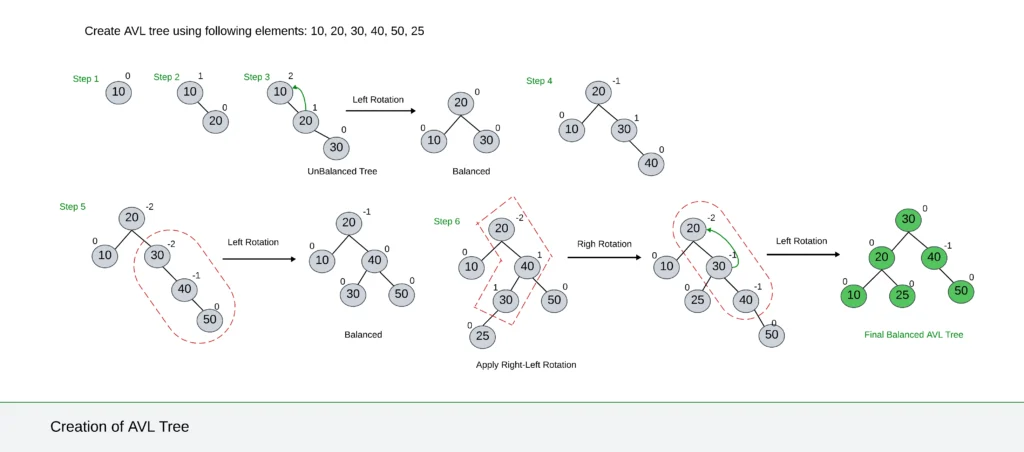
creation of avl tree
  1. Insert a new node as a leaf, following the rules of a binary search tree.
  2. Trace the path from the newly inserted node towards the root.
  3. For each node encountered, check if the height difference between its left and right subtrees exceeds 1 (balance factor, not -1, 0, or +1).
    • If the balance is maintained, move to the parent node.
    • When a node’s balance factor violates the AVL property, a rotation is performed to rebalance the tree.

Rotations:

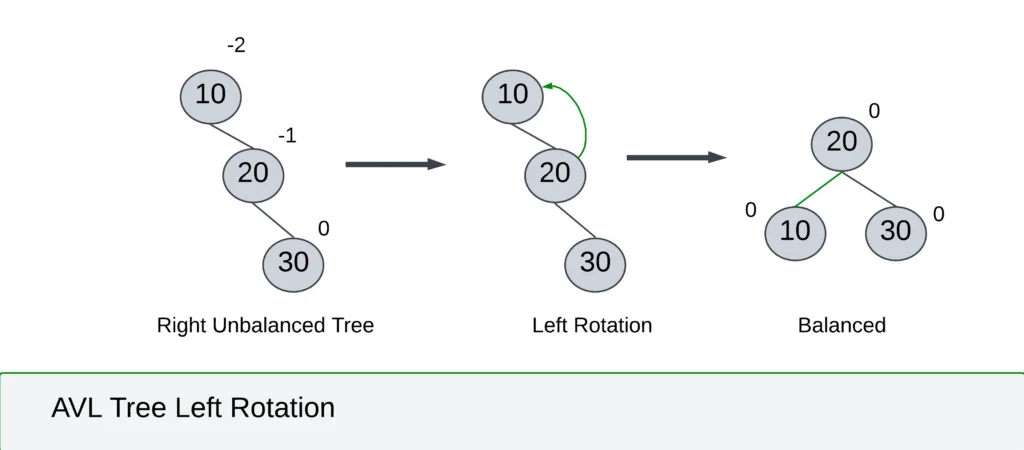
rotation of avl tree
  • Rotations are essential to rebalance the tree when the AVL property is violated during insertion or deletion. There are two types of rotations:
  • Single Rotation:
    • Left-Left (LL rotation)
    • Right-Right (RR rotation)
  • Double Rotation:
    • Left-Right (LR rotation)
    • Right-Left (RL rotation)
  • These rotations involve specific rearrangements of nodes to maintain the balance factor within the allowed range.

Deletion:

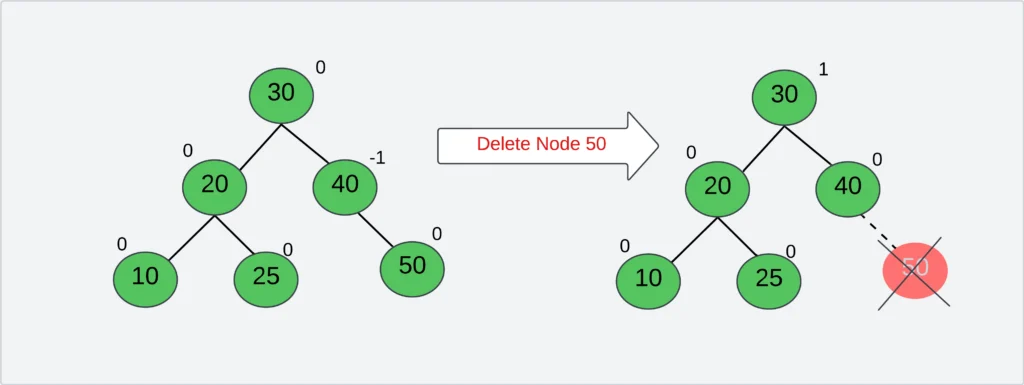
deletion of avl tree
  1. Search for the node to be deleted.
  2. If it’s a leaf node, remove it directly.
  3. If it’s not a leaf node (has one or two children), swap it with its in-order successor and then remove the swapped node.
  4. Traverse back up the path towards the root, checking the balance factor of each node.
  5. If an unbalanced subtree is encountered, perform the appropriate rotations to restore balance.

Searching:

Searching an AVL tree is identical to searching a binary search tree. The logarithmic height of the tree guarantees efficient search operations with O(log n) time complexity.

Advantages of AVL Trees:

  • Logarithmic time complexity for insertion, deletion, and search operations is guaranteed.
  • Maintains a balanced structure, ensuring efficient performance even in worst-case scenarios.

Disadvantages of AVL trees:

  1. Implementation Complexity: AVL trees are more complex to implement than standard BSTs due to the need for rotation operations to maintain balance.
  2. Balance Maintenance Overhead: Constantly maintaining balance through rotations introduces computational overhead, especially during insertion and deletion.
  3. Increased Memory Usage: Storing balance factors at each node in an AVL tree leads to higher memory consumption corresponding to regular BSTs.
  4. Potential Inefficiency for Write-Heavy Operations: The constant rebalancing might introduce performance bottlenecks for applications with frequent insertions and deletions.
  5. Traversal Speed: Traversing an AVL tree doesn’t offer significant speed improvements over traversing a standard BST.

Applications of AVL Trees:

AVL trees find applications in various domains where efficient data retrieval and storage are crucial:

  • In-memory databases.
  • Data structures for compilers and interpreters.
  • Autocomplete features in search engines and text editors.
  • Maintaining sorted data sets.

Conclusion:

AVL trees are a powerful data structure that combines the efficient searching capabilities of binary search trees with a self-balancing mechanism, ensuring consistent performance even with dynamic data sets. Their guaranteed logarithmic time complexity for fundamental operations makes them a valuable tool for developers and engineers across various fields.

1. What is the worst-case time complexity of operations on an AVL tree?

  • The main advantage of AVL trees is their guaranteed logarithmic performance. 
  • This means that search, insertion, and deletion operations all have a worst-case time complexity of O(log n), even in scenarios where a standard BST might degrade to linear time. 
  • This predictability makes AVL trees suitable for applications where consistent performance is crucial.

2. How do AVL trees compare to Red-Black trees?

  • While both AVL and Red-Black trees are self-balancing binary search trees, they differ in their approaches to maintaining balance.
  • AVL trees are stricter in maintaining balance, leading to potentially more rotations during insertion and deletion.
  • While Red-Black trees allow for a more relaxed balance, potentially reducing the overhead of rotations. 
  • In practice, Red-Black trees are often preferred for applications with frequent updates, while AVL trees might be favored when search operations are more frequent.

3. Can you give an example of when to choose an AVL tree over a hash table?

  • While both AVL trees and hash tables offer efficient search operations, they have different strengths. 
  • Choose an AVL tree when you need to maintain the order of elements and support operations like finding the minimum, maximum, or elements within a range, which are not efficiently supported by hash tables. 
  • If order is not a concern and you primarily need fast key-value lookups, a hash table might be more suitable.

4. How does the height of an AVL tree affect its performance?

  • The height of an AVL tree is directly related to its performance. 
  • Since AVL trees maintain a balanced structure, their height remains logarithmic to the number of nodes (log n). 
  • This logarithmic height ensures that search, insertion, and deletion operations can be performed efficiently, even for large datasets, as the number of nodes visited during these operations remains relatively small.

5. Are there any alternatives to AVL trees for maintaining sorted data?

  • While AVL trees effectively maintain sorted data, other data structures, such as red-black trees and B-trees, provide alternative approaches with their performance trade-offs.
  • Red-Black trees excel at maintaining a balance between efficient data retrieval and the complexity of inserting and deleting nodes.
  •  B-trees are commonly used in databases and file systems as they are optimized for disk-based storage. 
  • Skip lists offer a compelling blend of simplicity and efficiency, employing probabilistic balancing for easier implementation and delivering strong average-case performance.
Scroll to Top