Algorithm in Data Structure

/ What is an algorithm / What is  greedy algorithm

What is an Algorithm:

An Algorithm is a step-by-step procedure to obtain the solution of a particular task. 

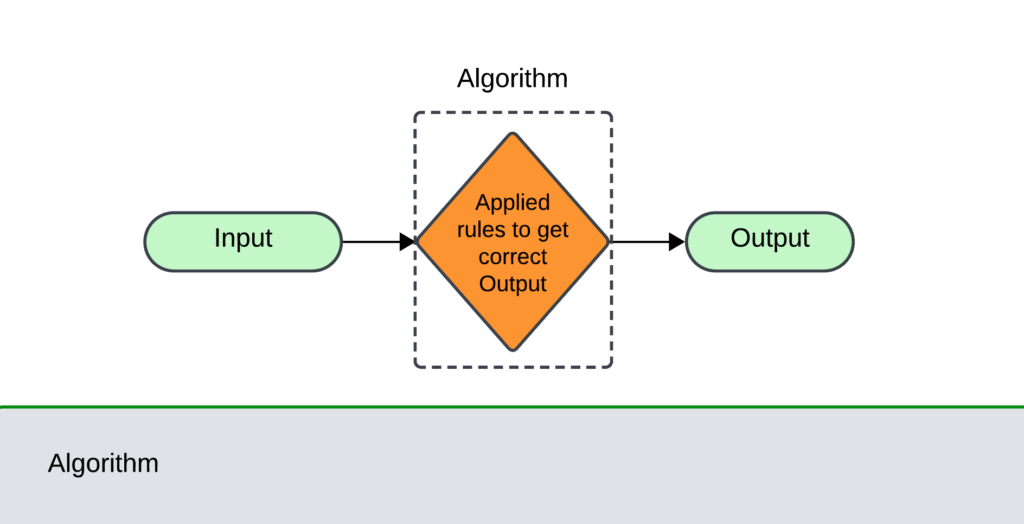
The characteristics of the algorithm are

1. Input: zero or more quantities are supplied as inputs to the algorithm.
2. Output: At least one quantity is displayed as output from the algorithm.
3. Definiteness: Each step in an algorithm should be very basic and clear.
4. Finiteness: After performing a certain number of steps the algorithm has to be terminated.
5. Effectiveness: Each step in the algorithm should be more effective.

The algorithm which we have written may be simple or complex. The complex algorithm in data structure is often divided into smaller units called modules. The process of dividing a complex algorithm into modules is called modularization.

The main advantage of modularization is

1. It makes the complex algorithm simpler to design and implement.
2. Each module can be designed independently.

Two approaches to designing an algorithm

Those are

1. Top-down approach
2. Bottom-up approach

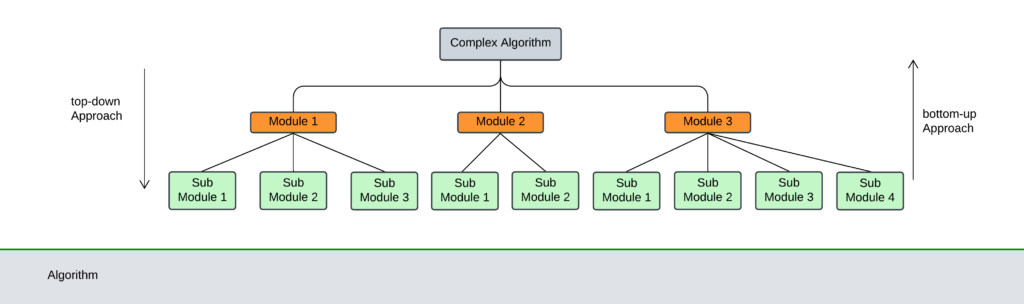
Top-down approach

• A top-down design starts by dividing the complex algorithm into one or more modules. 
• These modules are further decomposed into sub-modules and this process is repeated until the desired level of module complexity is achieved.

Bottom-up approach

• The bottom-up approach is just a revere of the top-down approach. 
• In the bottom-up approach, we start designing the most basic modules and then proceed towards designing the higher modules. 
• The sub-modules are grouped together to form a high-level module.

Control structures used in an Algorithm

An algorithm has a finite number of steps. An algorithm may employ one of the following control structures such as sequence, selection or decision-making, repetition, or iteration.

Sequence

Each step of an algorithm is executed step-by-step without causing any break.

Ex: 

Step 1: Start

Step 2: Read the value of a.

Step 3: Read the value of b.

Step 4: compute c=a+b.

Step 5: Display c

Step 6: stop.

Selection

Selection statements are used when the execution of a process depends on the outcome of some condition.

The selection statement is specified by using the if statement.

The syntax is

if(condition)
Statement 1;
else
Statement 2;

Ex: 

Step 1: Start

Step 2: Read the value of a.

Step 3: Read the value of b.

Step 4: if(a>b)

              Print a

               else

               Print b

Step 5: stop.

Repetition

Repetition means executing one or more statements for a number of times. These can be implemented by using while, do-while, for loops in C language.

Ex: Sum of first 10 natural numbers.

Step 1: Start

Step 2: set i=1, sum=0

Step 3: Repeat the steps 4 and 5 until i≤10.

Step 4: sum=sum+i.

Step 5: i=i+1

Step 6: print sum.

Step 7: stop.

Approaches/Types to Design an Algorithm

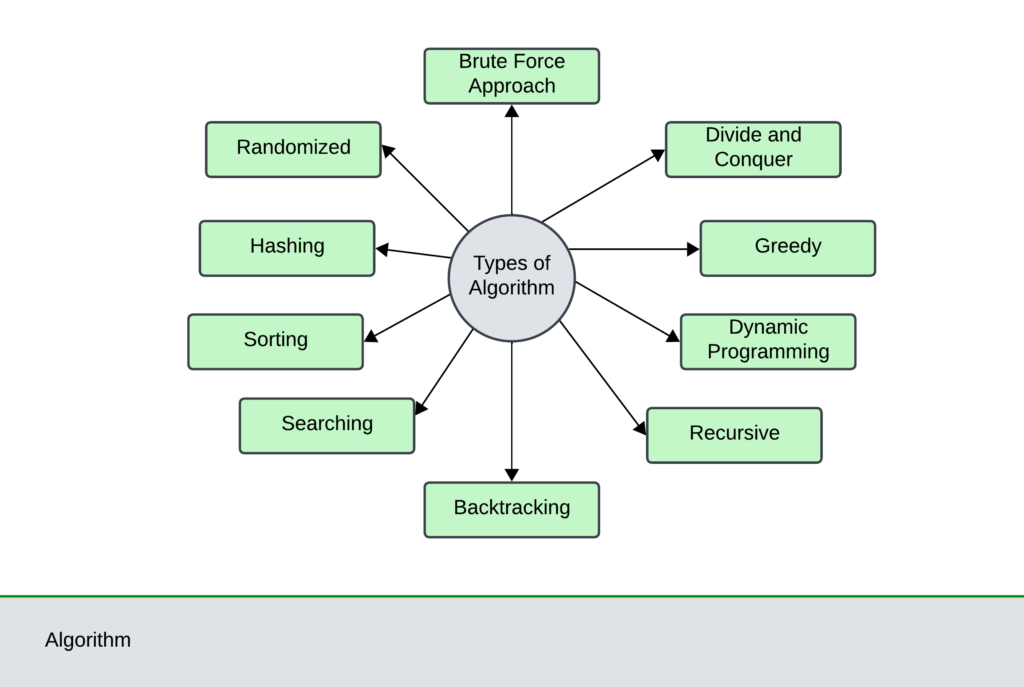
The different approaches to designing an algorithm are

1. Brute force approach

• The brute force approach is a straightforward approach to solving a problem based on the problem statement and definitions of the concepts involved. 
• It is considered one of the easiest approaches to apply and is useful for solving small instances of a problem.
  • Ex:   To calculate aⁿ where n>0.

• To calculate the factorial of a number n!
• Linear search, selection sort, and bubble sort are examples of brute-force approaches.

2. Divide and Conquer

• In this divide and conquer method, the problem is divided into smaller sub-problems and then each sub-problem is solved independently. 
• When we keep on dividing the sub-problem into event sub-problems then we reach a stage where there is no division which is possible.
• The smallest problem is solved. The solution of all sub-problems is finally merged in order to obtain the solution of the original problem.

Ex: binary search, merge sort, quick sort.

3. Greedy Method

• A greedy method is designed to achieve the optimum solution for a given problem. 
• They try to find a localized optimum solution which may eventually lead to a globally optimized solution.

Ex: Minimum spanning trees.

4. Dynamic Programming

• One of the disadvantages of divide and conquer is that the process of recursively solving separate sub-instances can result in computation time. 
• The idea behind dynamic programming is to avoid this pathology of obviating the requirement to calculate the same quantity twice. 
• This method usually maintains a table of sub-instance results. The results of smaller sub-problems are used for similar sub-problems. These algorithms are used in optimization.

Ex: Generating Fibonacci numbers using iteration.

5. Recursive Algorithm

• Breaks a problem into smaller sub-problems of the same type.
• Calls itself to solve the sub-problems.
• Efficient for problems with overlapping sub-structures.

6. Backtracking Algorithm

• Builds a solution step-by-step.
• Backtracks to previous steps if the current path leads to a dead end.
• Useful for finding all possible solutions or generating permutations.

7. Searching Algorithm

• Finds specific elements or groups of elements within a data structure.
• Different types exist based on the data structure and search criteria.
• Examples encompass linear search, binary search, and depth-first search

8. Sorting Algorithm

• Arrange a group of data in a specific order (e.g., ascending or descending).
• Various algorithms exhibit varying degrees of time and space complexity
• Illustrative examples encompass bubble sort, insertion sort, and quicksort.

9. Hashing Algorithm

• Uses a hash function to map keys to unique locations in a hash table.
• Efficient for searching and inserting elements.
• Might run into some snags if the hash function isn’t up to snuff, which could lead to some nasty collisions

10. Randomized Algorithm

• Uses random numbers to make decisions.
• Can be efficient for certain problems but may not always produce the same results.
• Examples include quicksort and randomized algorithms for finding minimum spanning trees.

Uses of Algorithm

1. Data Manipulation: Algorithms provide efficient ways to insert, delete, update, and retrieve data from various data structures. 

For example, search algorithms like binary search quickly locate elements in sorted arrays or trees.

2. Data Organization: Algorithms help maintain order and structure within data structures. 

Sorting algorithms arrange elements in a specific order while balancing algorithms maintain the balanced shape of trees for optimal performance.

3. Problem Solving: Algorithms are the building blocks for solving complex problems using data structures.

 Graph algorithms, for instance, can find the shortest path between nodes or detect cycles in networks.

4. Optimization: Algorithms often aim to minimize time and space complexity, ensuring operations on data structures are executed efficiently. 

For example, hashing algorithms enable fast lookups in hash tables.

5. Data Analysis: Algorithms can process and analyze data stored in data structures to extract meaningful insights or patterns. 

Machine learning algorithms, for example, can classify or cluster data points based on their features.

Specific Examples of Algorithm Uses in Data Structures

• Arrays: Sorting algorithms (e.g., quicksort, merge sort) arrange elements in ascending or descending order while searching algorithms (e.g., linear search, binary search) locate specific values.
• Linked Lists: Algorithms for insertion, deletion, and traversal enable efficient manipulation of linked lists.
• Trees: Tree traversal algorithms (e.g., inorder, preorder, postorder) visit nodes in a systematic order, while balancing algorithms (e.g., AVL tree rotation) maintain the balanced structure of trees for optimal search performance.
• Graphs: Graph algorithms (e.g., Dijkstra’s algorithm, breadth-first search) find shortest paths, detect cycles, or identify connected components in graphs.
• Hash Tables: Hashing algorithms map keys to unique indices for fast data retrieval.

Designing an algorithm

1. Understand the Problem: Clearly define the problem you’re trying to solve. Identify the inputs, desired outputs, and any constraints or requirements.
2. Choose the Data Structure: Select the appropriate data structure(s) that best represents the problem’s data and relationships. Consider factors like access patterns, insertion/deletion frequency, and search requirements.
3. Devise the Algorithm Logic: Develop the step-by-step instructions or procedures that manipulate the data structure to achieve the desired outcome. This often involves techniques like iteration, recursion, divide-and-conquer, or dynamic programming.
4. Analyze the Algorithm: Evaluate the algorithm’s correctness, efficiency, and resource usage. Determine its time complexity (how the runtime scales with input size) and space complexity (how much memory it consumes).
5. Refine and Optimize: Iteratively refine the algorithm to improve its performance or address any shortcomings. Consider alternative approaches, edge cases, and potential optimizations.
6. Implement and Test: Translate the algorithm into code using a suitable programming language. Thoroughly test the implementation with various inputs and edge cases to ensure correctness and reliability.

Advantages of algorithms in data structures

1. Efficiency: Algorithms optimize operations on data structures, minimizing time and space complexity for faster execution and reduced resource usage.
2. Correctness: Well-designed algorithms guarantee reliable and accurate results when manipulating or traversing data structures.
3. Scalability: Algorithms often handle varying input sizes effectively, ensuring performance remains consistent as data structures grow.
4. Reusability: Many algorithms are generalizable and can be applied to different data structure types, promoting code modularity and maintainability.
5. Abstraction: Algorithms provide a high-level approach to solving problems with data structures, shielding users from implementation details and focusing on core functionality.

Disadvantages of algorithms in data structures

1. Complexity: Some algorithms can be difficult to design, understand, and implement, especially when dealing with complex data structures or intricate problems.
2. Overhead: Algorithms may introduce computational overhead due to additional instructions or operations, potentially impacting performance in some scenarios.
3. Limitations: Certain algorithms might be optimized for specific data structures or operations, making them less suitable or efficient for other use cases.
4. Subjectivity: Choosing the right algorithm often involves trade-offs between different factors like time complexity, space complexity, and implementation difficulty, leading to subjective decisions based on specific requirements.
5. Inflexibility: Some algorithms might not easily adapt to changes in the underlying data structure or problem domain, requiring modifications or complete redesign.

FAQs on Algorithm in Data Structure

Q1. What is the difference between time complexity and space complexity?

• Time complexity: Describes how an algorithm’s runtime scales with the input size, often expressed using Big O notation (e.g., O(n), O(log n), O(n^2)).
• Space complexity: Describes how much memory an algorithm uses as the input size grows, also expressed using Big O notation.

Q2. Can you explain the difference between a stack and a queue?

• Stack: Follows the Last-In-First-Out (LIFO) principle, where the last element added is the first to be removed (like a stack of plates).
• Queue: Follows the First-In-First-Out (FIFO) principle, where the first element added is the first to be removed (like a line of people waiting).

Q3. What are some common sorting algorithms, and what are their time complexities?

• Bubble Sort: O(n^2)
• Insertion Sort: O(n^2) (but efficient for small or nearly sorted lists)
• Merge Sort: O(n log n)
• Quick Sort: O(n log n) (average case), but can degrade to O(n^2) in the worst case
• Heap Sort: O(n log n)

Q4. How does a hash table work, and what are its advantages?

• Hash Table: Uses a hash function to map keys to indices in an array for fast data retrieval (average O(1) lookup time). Advantages include efficient insertion, deletion, and searching.

Q5. Could you describe a situation where you would use a graph data structure, and what algorithm would you choose to solve a problem with it?

• Graph Use Case: Representing social networks, transportation networks, or dependencies between tasks.
• Algorithm Example: Dijkstra’s algorithm for finding the shortest path between two nodes in a graph.

Related topics:

• Towers of Hanoi Algorithm | Program