The sampling Theorem is a band-limited signal x(t), with maximum frequency W Hz, fully represented by samples taken at 1/(2W) seconds.
AND
A band-limited signal, x(t), with frequencies not exceeding W Hz, can be perfectly reconstructed from samples acquired at a rate of 2W samples per second.
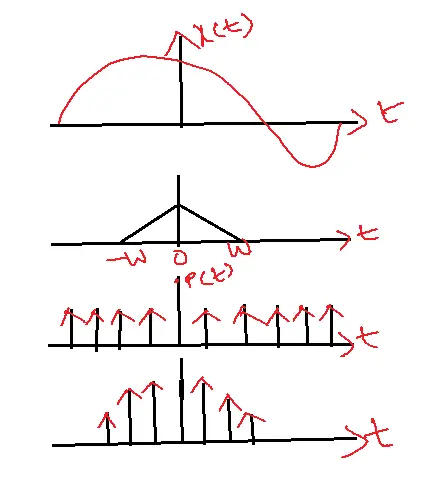
Table of Contents
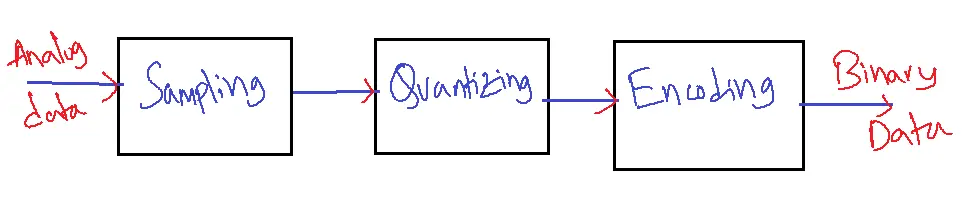
The Sampling Theorem defines the minimum sampling rate for accurate analog-to-digital signal conversion.
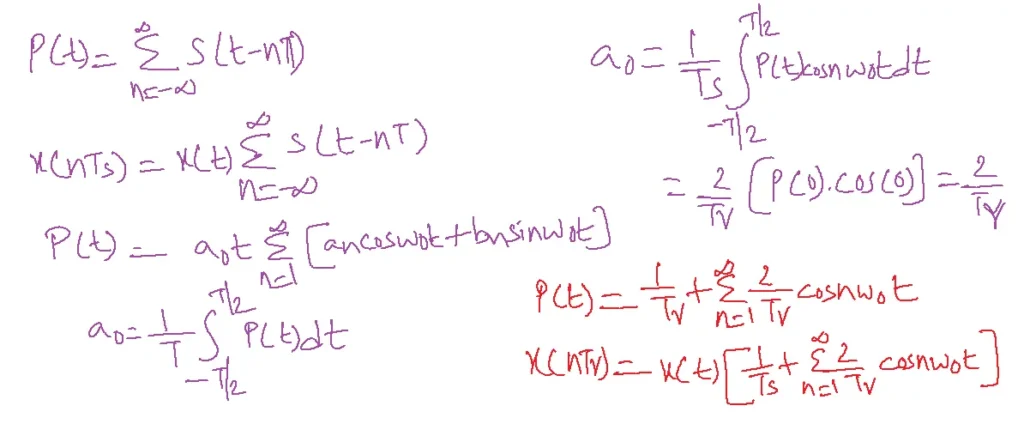
To prevent information loss and ensure precise reconstruction, the Nyquist sampling theorem mandates a minimum sampling rate (fs) twice the highest frequency component (fa) present in the signal.
Nyquist Sampling Rate:
In mathematical terms, the lowest Nyquist sampling rate is fs ≥2fa, where fs is the lowest Nyquist sampling rate in Hz and fa is the highest analog input frequency in Hz.
Aliasing, or folding, occurs when the sampling frequency (fs) is less than twice the maximum frequency component of the analog signal (fa), expressed as fs < 2fa. This can be fixed by suppressing the component before sampling with an anti-aliasing filter.
Natural Sampling
Natural sampling involves capturing the analog waveform’s amplitude during the sampling pulse, leading to a sampled output with a distinct frequency spectrum that differs from the ideal sampled signal.

Flat-top sampling:
A sample-and-hold circuit is used to complete the process. Its goal is to convert the continuously fluctuating analog input voltage into a sequence of constant PAM voltage levels by regularly sampling the input voltage. In flat-top sampling, a brief pulse is used to capture the input voltage, and then the sampled value is held steady until the next sampling pulse occurs.
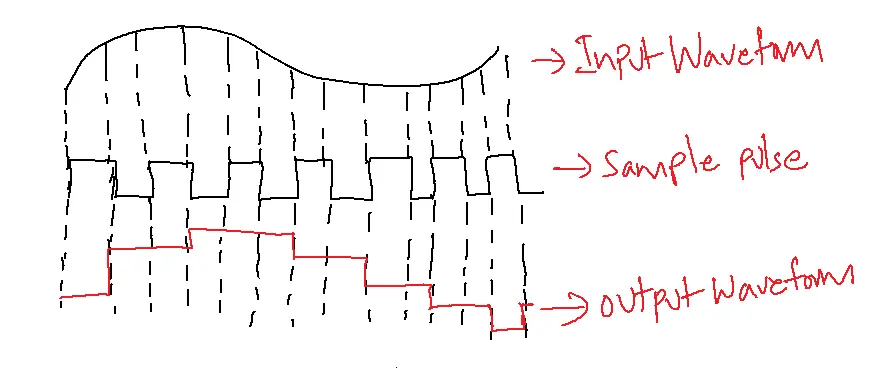
Flat-top sampling offers improved performance over natural sampling, with reduced aperture distortion and the ability to operate with a slower analog-to-digital converter.
SAMPLING RATE:
According to the Nyquist sampling theorem, the minimum sampling rate, fs, must be twice the higher input frequency, fa, for a sample to be repeated properly. The lowest Nyquist sampling rate, or fs, may be expressed mathematically as fs ≥ 2 fa, where fa is the maximum analog input frequency in hertz and fs is the minimum Nyquist sample rate.
Foldover or aliasing distortion occurs when the sampling rate is insufficient, specifically when fs is less than 2fa. To get around this, suppress the component before sampling using an anti-aliasing filter.
Key Points:
1. Sampling Rate: Sample analog signals at least twice their highest frequency to meet the Sampling Theorem’s requirements.
2. Nyquist Rate: This minimum sampling rate is called the Nyquist rate.
3. Aliasing: Sampling at a rate lower than the Nyquist rate results in aliasing, which distorts the signal and leads to errors.
4. Signal Reconstruction: Sampling at the Nyquist rate allows for perfect reconstruction of the original analog signal from the digital samples.
Importance:
1. Digital Signal Processing: This theorem is crucial for digital signal processing applications, such as audio and image processing.
2. Data Acquisition: It ensures accurate data acquisition and representation in digital systems.
3. Communication Systems: The Sampling Theorem is essential for designing communication systems, including modems and digital telephony.
Formula:
f_s ≥ 2f_max
Where:
– f_s is the sampling rate
– f_max is the highest frequency component of the analog signal
Advantages of Sampling Theorem in Digital Communications:
1. Accurate Signal Representation: The sampling Theorem ensures accurate representation of analog signals in digital form.
2. Efficient Data Compression: It facilitates compact data representation, minimizing storage space and transmission bandwidth.
3. Improved Signal Processing: Sampling Theorem facilitates advanced signal processing techniques, enhancing signal quality and analysis.
4. Simplified System Design: It simplifies digital communication system design, ensuring reliable data transfer and processing.
5. Flexible Sampling Rates: The Sampling Theorem allows for flexible sampling rates, accommodating various signal types and applications.
Disadvantages of Sampling Theorem in Digital Communications:
1. Aliasing Distortion: Sampling at rates lower than the Nyquist rate causes aliasing distortion, leading to signal errors.
2. Increased Complexity: Higher sampling rates increase system complexity, requiring more advanced hardware and processing power.
3. Higher Bandwidth Requirements: The Sampling Theorem requires higher bandwidth to accommodate increased sampling rates, potentially leading to data transmission challenges.
4. Quantization Noise: Sampling introduces quantization noise, affecting signal quality and accuracy.
5. Limited Dynamic Range: The Sampling Theorem has limited dynamic range, making it less suitable for signals with large amplitude variations.
Applications of Sampling Theorem in Digital Communications:
1. Digital Telephony: The Sampling Theorem is used in digital telephony to convert analog voice signals to digital signals for efficient transmission.
2. Digital Audio: It is used in digital audio systems, such as CDs and MP3s, to convert analog audio signals to digital signals.
3. Digital Image Processing: The Sampling Theorem is applied in digital image processing to convert analog to digital images.
4. Digital Video: Digital video systems, such as DVDs and streaming services, utilize the Sampling Theorem to transform analog video signals into digital data.
5. Data Acquisition Systems: Sampling Theorem is used in acquisition systems to convert analog sensor data to digital data.
6. Medical Imaging: It is applied in medical imaging techniques, such as MRI and CT scans, to convert analog signals to digital images.
7. Radar and Sonar Systems: The Sampling Theorem is used in radar and sonar systems to convert analog signals to digital signals for processing and analysis.
8. Digital Modems: It is used in digital modems to convert analog signals to digital signals for efficient data transmission.
9. Satellite Communications: The Sampling Theorem is applied in satellite communications to convert analog signals to digital signals for efficient transmission.
10. Digital Signal Processing: It is used in digital signal processing techniques, such as filtering and analysis, to convert analog signals to digital signals.
FAQs of Sampling Theorem:
1. What is the Sampling Theorem?
- The Sampling Theorem, also called the Nyquist-Shannon theorem, is a cornerstone principle in signal processing.
- A continuous-time signal can be reconstructed from its sampled values if the sampling frequency is at least twice the highest frequency component in the signal.
2. Why is the Sampling Theorem important in digital communications?
- The Sampling Theorem allows for the lossless conversion of analog signals into the digital domain, a crucial process in digital audio, video, and communication systems.
3. What is the Nyquist rate?
- Nyquist rate: minimum sampling rate for perfect signal reconstruction. Equals twice the highest frequency component. The sampling below causes aliasing.
4. What is aliasing and how can it be prevented?
Aliasing occurs when a signal is sampled reduced than the Nyquist rate. It results in distortion and loss of information in the reconstructed signal. To prevent aliasing, we can either:
- Increase the sampling rate: To avoid aliasing, ensure the sampling rate is no less than twice the highest frequency contained in the signal.
- Use an anti-aliasing filter: Filter out frequencies above half the sampling rate before sampling.
5. What are the applications of the Sampling Theorem?
- Analog-to-digital conversion (ADC) is a fundamental process in various fields.
- It involves converting analog signals, such as audio, video, voice, medical imaging, and sensor data, into digital format.
- The main applications of ADC include:
- Digital audio and video
- Telecommunications
- Medical imaging
- Data acquisition systems
- ADCs facilitate the efficient storage, transmission, and analysis of data by transforming analog signals into their digital counterparts.
