Quantization converts continuous amplitude signals into discrete amplitude signals.
It is of two types:
1. Linear or uniform
2. Non-linear or Non-uniform
Linear or Uniform Quantization
Depending upon transfer characteristics, there are three types of uniform quantization
1. Mid-tread
2. Mid riser
3. Biased
Table of Contents
Mid-tread Quantization
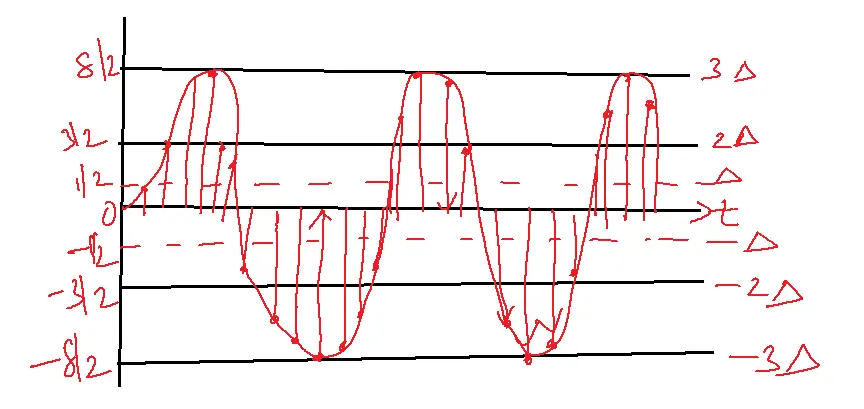
Transfer characteristics:
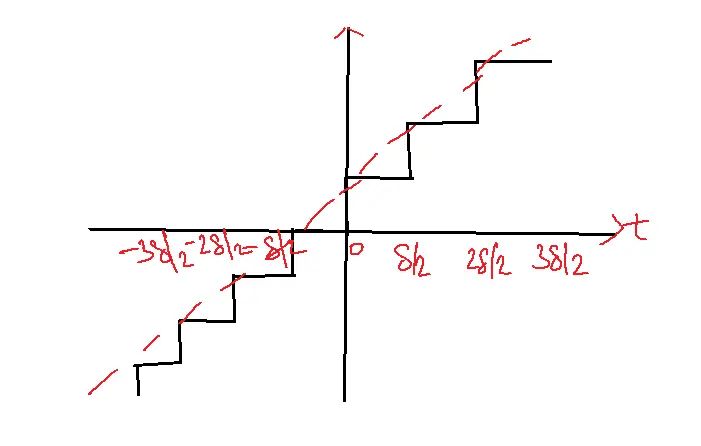
x(nTs)=0, quantized error
x(nTs)= delta/2, Maximum error
Quantization error=xg(nTs)-x(nTs)

Mid-rise Quantization
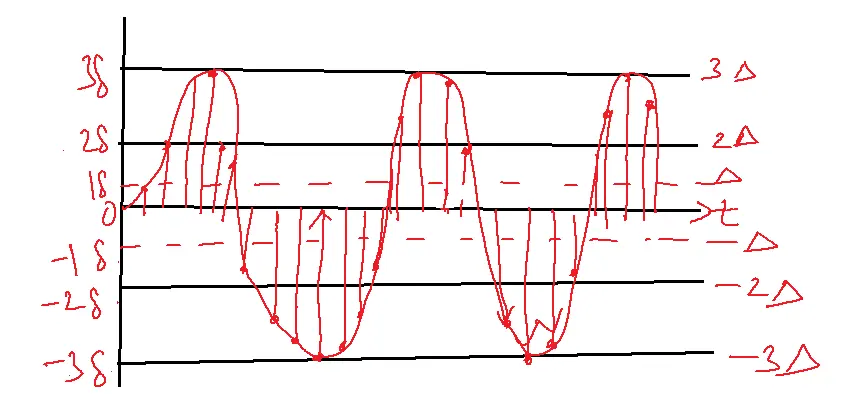
Transfer characteristics:
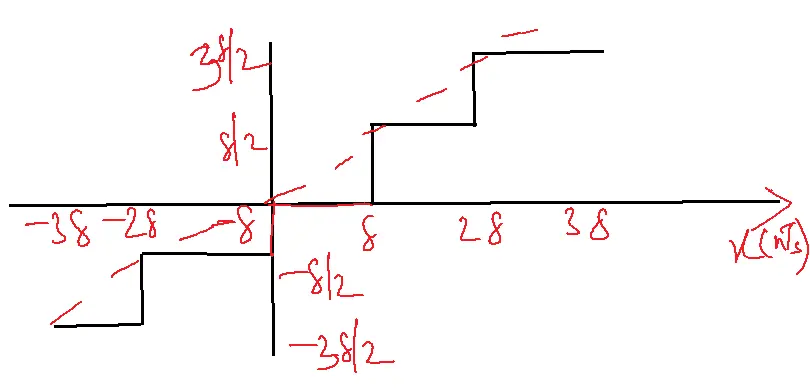
Qe=xq(nTs)-x(nTs)
Biased quantization and transfer characteristics
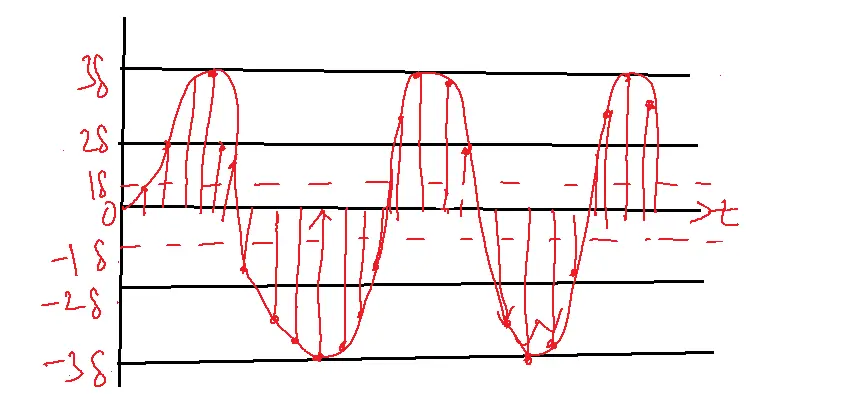
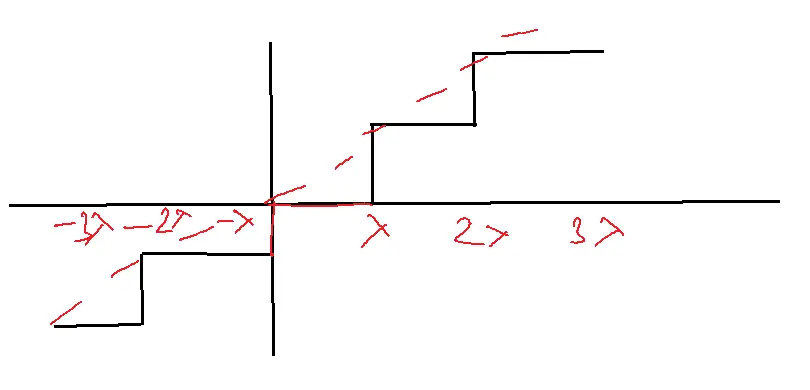
Quantization and the folded Binary Code
- The process of transforming a continuous range of values into a discrete, finite set of values is known as quantization.
- This is a feature of analog-to-digital converters, which turn an analog signal into a sequence of digital values.
- It is necessary to transform the analog signal into a limited number of PCM code possibilities.
- Take, as an illustration, a sine wave that passes between +5V and -5V and has a peak amplitude of 5V via each amplitude that exists between them.
- There could only be eight bits in a PCM code, meaning it corresponds to just 28 or 256 permutations, and the sine wave values must be completed.
| Sign | Magnitude | Decimal Value | Quantization Range |
| 1 | 11 | +3 | +2.5 – +3.5 |
| 1 | 10 | +2 | +1.5 – +2.5 |
| 1 | 01 | +1 | +0.5 – +1.5 |
| 1 | 00 | +0 | +0 – +0.5 |
| 0 | 00 | -0 | -0 – -0.5 |
| 0 | 01 | -1 | -0.5 – -1.5 |
| 0 | 10 | -2 | -1.5 – -2.5 |
| 0 | 11 | -3 | -2.5 – -3.5 |
- The three-bit PCM code, which consists of four +ve and four -ve potential permutations, is displayed in the above table.
- The sign bit (1 = + and 0 = -) is located at the leftmost bit, while the magnitude is represented by the final two bits on the right.
- Because the codes on the bottom half of the table, except the sign bit, are an identical mirror copy of the codes on the top, this sort of coding is known as folded binary code.
- Its interval, known as quantum (1V for the above table), is the magnitude difference between consecutive steps.
- The highest signal magnitude that may be encoded for the code is +3V (111) or -3V (011), while the lowest is +1V (101) or -1V (001).
- Peak limiting, another name for overload distortion, occurs when the sample size exceeds its maximum interval.
- Quantizing is the process of assigning PCM codes to absolute magnitudes. Another name for a quantum’s magnitude is its resolution.
- It is equivalent to the PCM code’s least significant bit (Vlsb) voltage. The quantized signal will more closely match the original analog signal and have greater resolution the lower the quantum’s magnitude.
- After rounding each sample voltage to the nearest level, it is translated into the appropriate PCM code.
- Essentially, the PAM signal generated in the transmitter and the receiver are identical.
- Therefore, any round-off mistakes in the broadcast signal are replicated when the receiver’s DAC converts the code back to analog.
- This defect is known as quantization noise (Qn), or quantization error (Qe).
- With only three samples extracted from the analog signal, a three-bit PCM coding, and inadequate resolution.
- The quantized signal seen above closely matches the original input signal.
As previously demonstrated, employing a PCM coding with additional bits can enhance the quality of the PAM signal by decreasing the quantum’s size and increasing its resolution. Furthermore, by sampling the analog data more quickly, the PAM signal improves quality and closely resembles the analog signal.
Qe is given by
Qe= VMIN/2 = RESOLUTION/2
DYNAMIC RANGE
The biggest possible magnitude to the smallest possible magnitude (apart from 0V) is the ratio that the receiver’s digital-to-analog converter can decode.
DR= VMAX/VMIN
Vmax is the highest voltage magnitude, the receiver’s DACs can detect, Vmin is the quantum value (resolution), and DR is the dynamic range.
Dynamic Range can be expressed in decibels as
DRdB= 20 log10(Vmax/Vmin)
OR
DRdB=20 log(2n-1)
Where n is the number of PCM bits.
Quantization Noise power
X(nTs)— -A to +A
L number of levels in quantization
2n =L
n=log2(L)
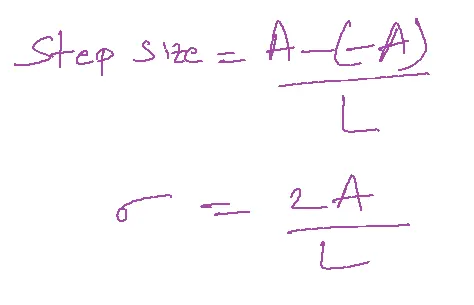
QE =xg(nTs)-x(nTs)


2n =L
In terms of the Number of bits
Noise Power = 4A2/12 x L2 = A2/3L2
Qn power=A2/3 X 22n
Advantages
1. Reduced Memory Requirements: It reduces the number of bits required to represent a signal, resulting in lower memory requirements.
2. Improved Processing Speed:It enables faster processing speeds, as fewer bits need to be processed.
3. Error Tolerance: It can provide error tolerance, as small errors in the signal can be ignored.
4. Simplified Hardware: It can simplify hardware design, as fewer bits need to be processed.
5. Compressed Data: It compresses data, making it easier to store and transmit.
Disadvantages
1. Loss of Information: It results in a loss of information, as the signal is approximated.
2. Distortion: It can introduce distortion, degrading signal quality.
3. Limited Dynamic Range: The signal’s dynamic range is constrained by it.
4. Non-Linear Effects: It can introduce non-linear effects, affecting signal processing.
5. Dependence on Step Size: Its performance depends on the step size, requiring careful selection.
Applications
- Analog-to-Digital Conversion (ADC): It is used in ADC to convert continuous analog signals into discrete digital forms, enabling digital signal processing applications.
- Digital Audio and Video: It compresses audio and video, enabling storage and transmission of large multimedia files over networks.
- Image Compression: It compresses images by reducing colors while maintaining visual quality.
- Data Compression: It is used in data compression to optimize storage and transmission efficiency by representing data with fewer bits while maintaining accuracy.
- Machine Learning and Deep Learning: It is used in machine learning to reduce computational complexity and memory requirements, enabling faster inference and efficient deployment on resource-constrained devices.
FAQs
1. What is quantization in digital communication?
- It transforms a continuous analog signal into discrete digital levels.
- It’s a crucial step in analog-to-digital conversion (ADC), enabling the representation of analog signals in a digital format.
2. Why is quantization important in digital communication?
- It is essential for:
- Digital representation of analog signals: It allows analog signals (like voice or music) to be processed, stored, and transmitted digitally.
- Data compression: Audio, video, and images can be efficiently compressed through this technique, as it decreases the number of bits required for their representation.
- Digital signal processing: It facilitates various signal processing operations in the digital domain, such as filtering, amplification, and modulation.
3. What are the types of quantization errors?
- The main types of quantization errors are:
- Quantization Noise: The difference between the original analog and the quantized digital value, introduces noise into the signal.
- Clipping or overload distortion: Occurs when the analog signal exceeds the maximum representable value in the quantizer, leading to signal clipping.
4. How does quantization affect the quality of digital signals?
- The quality of digital signals is influenced by the number of its levels (bits) used.
- Increasing the number of bits improves its accuracy and reduces noise but at the expense of larger data size.
- The choice of its levels involves a trade-off between signal quality and data storage or transmission requirements.
5. What are the techniques to improve quantization performance?
- Several techniques can be employed to improve quantization performance:
- Non-uniform quantization: Assigns more levels to regions with higher signal probability.
- Companding: Compresses the input signal before quantization and expands it after, reducing quantization noise in low-amplitude signals.
- Dithering: Adds a small amount of noise to the signal before quantization, reducing the perceived distortion.
