Open-loop control system: In an open-loop control system, the output does not influence system performance, making it impossible to verify if the desired outcome is achieved.
Closed loop control system: In a closed loop control system feedback is taken from the output of a system to monitor whether the outcome is controlled.
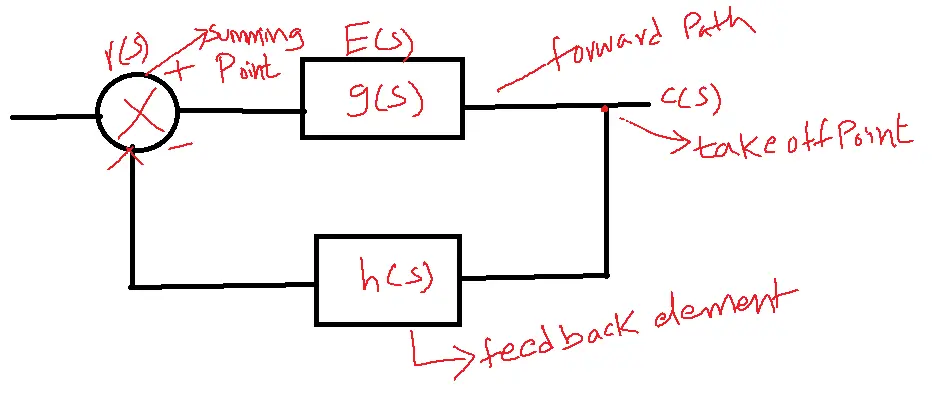
E(s) represents the error signal.
g(s) represents forward path gain.
h(s) represents the feedback element. The feedback element could be positive or negative.
Table of Contents
The transfer function of the closed-loop control system:
TF=c(s)/r(s)
If E(s)=0, the output is controlled. Otherwise, the output is not controlled.
E(s)=r(s)±h(s)c(s) —1
C(s)=E(s) X g(s) —2
1 in 2
c(s)/r(s) = g(s)/1±h(s)g(s)
The closed-loop control system is divided into two types:
1. Negative Feedback closed-loop control system
2. Positive Feedback closed-loop control system.
Negative Feedback Closed-loop Control System:
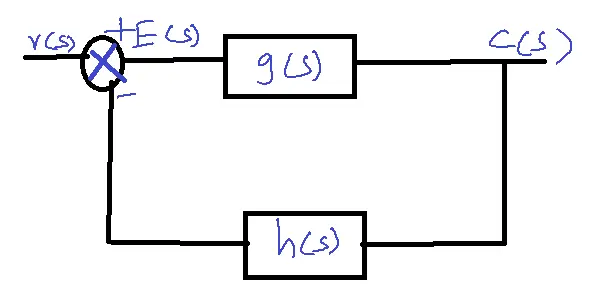
Transfer Function = c(s)/r(s) = g(s)/1+g(s)h(s)
Positive Feedback Closed-loop Control System:
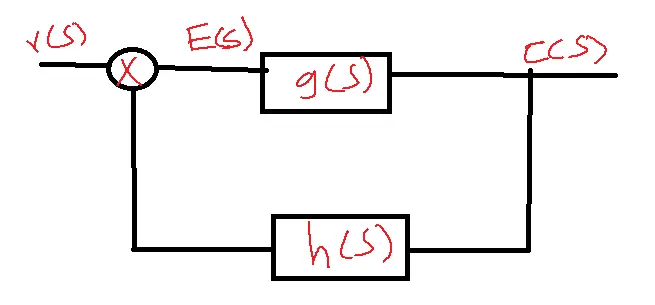
c(s)/r(s) = g(s)/1-g(s)h(s)
For the unity feedback system, h(s)=1, then the transfer function is c(s)/r(s) = g(s)/1-g(s).
Example: Determine the transfer function of the closed-loop control system shown in the below figure.
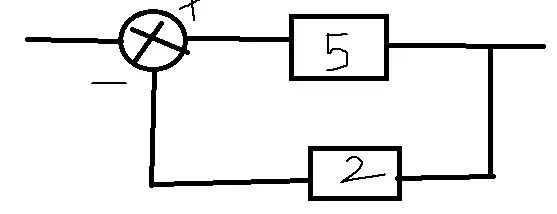
Solution: Transfer Function = c(s)/r(s) = g(s)/1+g(s)h(s)
5/1+(5X2) = 5/1+10 =5/11.
Comparison between open loop control system and closed loop control system:
| Open loop control system | closed-loop control system |
| Any changes in the output do not affect the input i.e., feedback does not exist. | Changes in the outcome affect the input which is possible by using feedback. |
| Output measurement is not required for the operation of a system. | Output measurement is needed. |
| There is no error detector in the open loop. | An error signal is required in a closed loop. |
| It is inaccurate and unreliable. | Highly accurate and reliable. |
| Sensitive to environmental changes. | Less sensitive to environmental changes. |
| The bandwidth is small. | Bandwidth is high. |
| Simple to construct and cheap. | Complicated to design and costly. |
| Generally, open-loop systems are stable. | Stability is the major consideration in designing a closed-loop system. |
| Highly affected by non-linearity. | Reduces effect on non-linearity. |
Effect of feedback/Feedback characteristics of open-loop control system:
1. Gain
2. Location of pole/stability
3. Time constant
4. Parameter variation
5. Noise effect
1. Effect of feedback on gain:
Consider an open loop control system, the gain of the system is c(s)/r(s) = g(s)
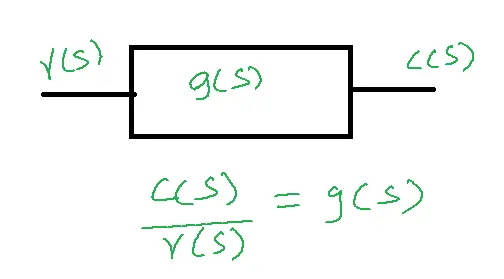
Consider a negative feedback control system the transfer function is c(s)/r(s) = g(s)/1+g(s)h(s)
with feedback, the gain of the system is decreased by a factor of 1+g(s)h(s)
2. Effect of feedback on the Location of the pole(stability):
The stability of the control system depends on the location of the pole.
If a system is more stable, the pole is located away from the origin.
Ex: Consider an open loop system with transfer function 1/s+100
c/r=1/s+100
In a given transfer function the roots of the numerator polynomial are known as zeroes.
The roots of the denominator polynomial are known as poles.
Convert the open loop system into a closed loop unity feedback system.
With feedback, the pole is away from the origin. Therefore the system is more stable.
3. Effect of feedback on Time constant:
The performance of a control system depends on the time constant. A short-time constant results in rapid control of the output by the system.
The time constant indicates the time required to control the system response.
Consider an open loop with feedback 1/s+10.
ApplyILT e-10t
Convert the open loop system into a closed loop with h(s)=10. The transfer function is 1/s+20.
Apply ILT to e-20t
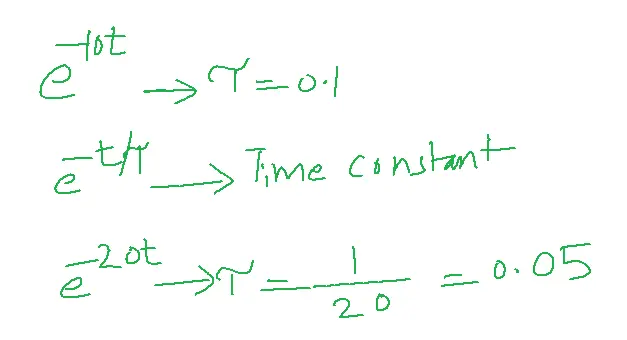
With feedback, the time constant is decreased and hence system takes very little time to control the output compared to the open loop system.
4. Effect of feedback due to parameter variation:
Consider an open loop system with gain g(s). assume that g(s) is varied.
Such output is given in the below figure.
Consider a closed-loop system with feedback element h(s). The transfer function for this system can be obtained from the open-loop transfer function depicted in the following figure.
5. Effect of Feedback on Noise:
Consider an open loop system with gain g(s)
Let n(s) represent the noise signal.
The transfer function of an open loop system is
c(s)=r(s)g(s)+n(s)g(s)
consider a closed-loop system with a negative feedback
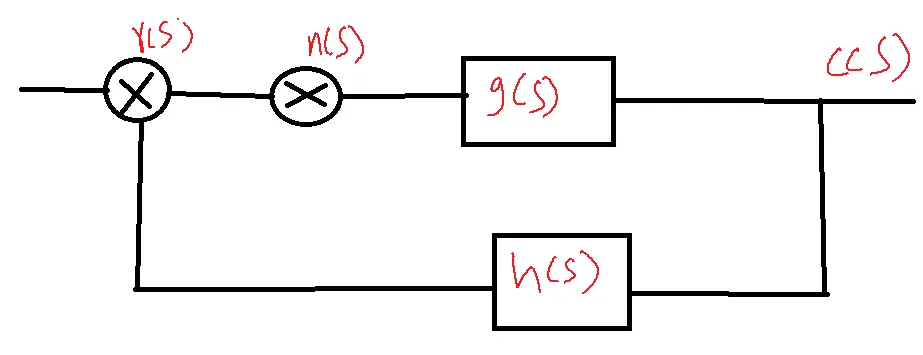
Here there are two inputs r(s) and n(s).
The superposition principle allows us to determine the system’s response to two inputs by considering the response to each input individually and then summing the results.
The total response= Response due to r(s)+Response due to n(s)
c(s)/R(s)=g(s)/1+g(s)h(s)
c(s)/R(s)=g(s)R(s)/1+g(s)R(s)
c(s)/R(s)= [N(s)G(s)/1+g(s)h(s)]+[R(s)G(s)/1+g(s)R(s)]
Due to feedback, the effect of noise is reduced.
Applications
Open-Loop Control System:
- Automatic Washing Machines: Preset timers control washing cycles without feedback on the cleanliness of clothes.
- Electric Hand Dryers: Operate for a fixed duration after activation, regardless of hand dryness.
- Bread Toasters: Heating elements activate for a predetermined time, assuming consistent browning.
- Traffic Lights: Follow a pre-programmed timing sequence to control traffic flow.
- Irrigation Systems: Water sprinklers operate on a fixed schedule without sensing soil moisture.
Closed-Loop Control System:
- Air Conditioners (ACs): Thermostats continuously monitor room temperature and adjust cooling accordingly to maintain a desired setpoint.
- Missile Guidance Systems: Continuously track the target and adjust trajectory for accurate interception.
- Voltage Stabilizers: Monitor output voltage and adjust input to maintain a stable voltage level.
- Process Control in Industries: Regulate temperature, pressure, flow rate, and other variables in chemical plants, refineries, and manufacturing processes.
- Motor Speed Control: Use feedback mechanisms to maintain a constant motor speed despite varying loads.
FAQs related to the topic
Q1. What is the difference between open-loop and closed-loop control systems?
- Open-loop systems operate without feedback, while closed-loop systems utilize feedback to monitor and adjust the output.
- This fundamental difference impacts accuracy, stability, and responsiveness.
Q2. What are the advantages and disadvantages of open-loop control systems?
- Open-loop systems are simpler, cheaper, and easier to implement.
- However, they are less accurate, sensitive to disturbances, and cannot correct errors.
Q3. What are the advantages and disadvantages of closed-loop control systems?
- Closed-loop systems offer improved accuracy, stability, and robustness to disturbances.
- However, they can be more complex, expensive, and prone to instability if not designed properly.
Q4. What are some real-world examples of open-loop control systems?
- Common examples include automatic washing machines, electric hand dryers, bread toasters, and traffic lights, where precise control is not critical.
Q5. What are some real-world examples of closed-loop control systems?
- Applications include air conditioners, missile guidance systems, voltage stabilizers, industrial process control, and motor speed control, where accuracy and stability are paramount.
