Information Theory is based on the concepts related to statistical properties of source, channel, and noise.
The signal power, channel noise, and bandwidth are available, we can estimate the condition for error-less transmission.
The amount of information carried by the channel successfully is called Mutual Information.
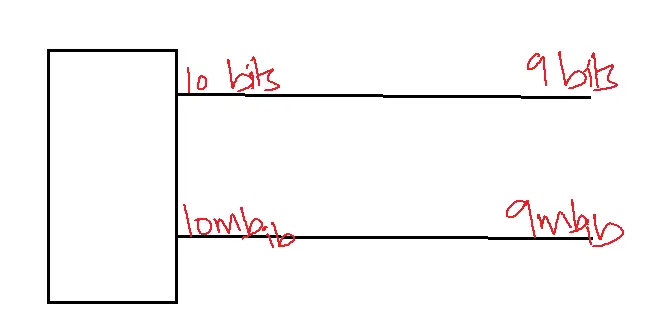
Mutual Information = source information – channel information
Mutual Information = 9 mb.
Table of Contents
Information
Information of the message is inversely proportional to the probability of the message.
Iα1/P
IK=log2(1/PK)
Discrete source M={M1, M2, M3,…..Mk}
P={P1,P2,P3,…..Pk}
Properties of Information
1. The message has more uncertainties or surprises, and the amount of information is more.
2. If the receiver knows the message, the information is zero.
3. If I1 is the information transmitted through message m1 , I2 is the information carried by the message m2 the information carried combinly by m1 and m2 is equal to I1 + I2.
4. Each message will carry n bits of information if there are N=2n equal likelihood messages.
Example
Calculate the amount of information in message m the probability is ¼.
Solution: I=log2(1/P)
I=log2(1/(1/4))
=log2(4)
=2 log2(2)
=2 bits.
Information Rate
The information rate is the number of bits of information, that the source generates in a second.
R=r x H
H-entropy
r-symbol rate
R=symbols/sec X bits/symbol
R=bits/sec.
Example: A discrete source generates 3 symbols x1,x2,x3 if the probability is ½,1/4,1/4 respectively. The symbol rate is 5000 symbols/sec. calculate the information rate.
Solution:
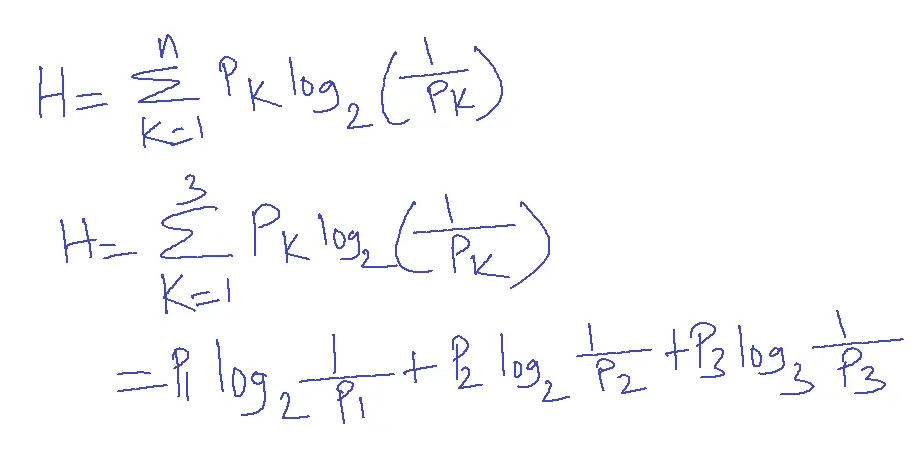
H=3/4
R=5000 x ¾=7500 bits/sec.
Example: Black and white TV contains 2 x 106 pixels per picture. Each pixel has 16 brightness levels. The pixels are transmitted at a rate of 32 pictures per second. All the brightness levels have equal probabilities. calculate the information rate.
Solution: N=16
Number of signals travelled per second r=32 x 2 x 106
=64 x 106
H=log2N = log216 = 4
R=rH
=64 x 106 x 4= 256 M bits /pixel
=256 Mbps.
Joint Entropy
Let a discrete source generate two symbols x1 and x2. Let y1 and y2 be the destinations for the received symbol.
The entropy of both transmitter and receiver is called joint entropy. H(x,y)
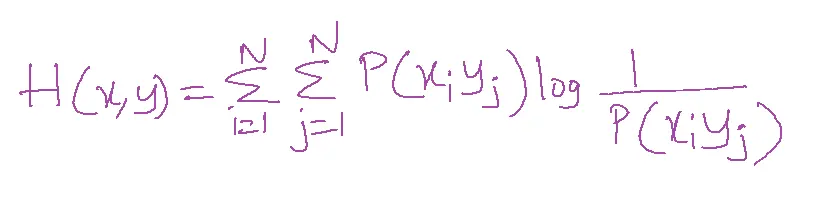
Conditional Entropy
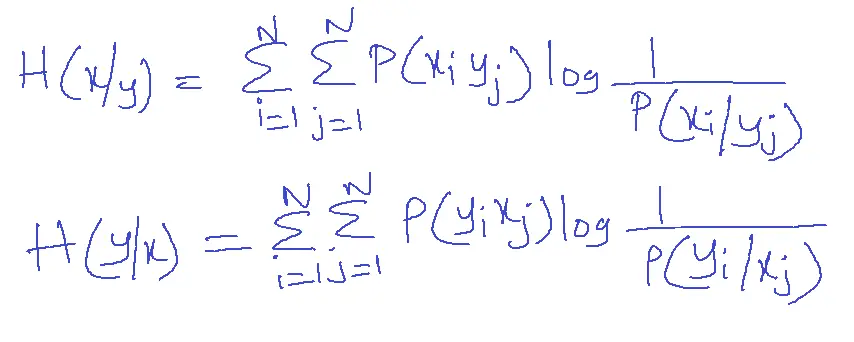
Mutual Information
The amount of information carried through the channel[successfully] is called Mutual Information.
Mutual information = Source – bits loss during channel
x1→y1
x1→y2
P(x1/y2)=log 1/P(x1/y2)
I(x1)=log 1/P(x1)
I(x1,y1)=log 1/P(x1) – log 1/P(x1/y2)
I(x1,y1)=log P(x1/y2)/P(x1)

Channel Capacity
Channel capacity is the greatest quantity of information that a channel can successfully carry.
C=max(I(x,y))bits/symbol
Shannon Hartley Capacity Theorem
Shannon Hartley Capacity theorem is defined as the capacity of a channel that bandwidth B and additive white Gaussian noise (N) is
Capacity
C = B log10(1+S/N)
Example: Calculate the capacity of a low pass channel with a usable bandwidth of 3000 Hz and signal-to-noise ratio=103 at the channel output. Assume the channel noise is Gaussian and white.
Solution: C=3000 log10(1+103)
C=9000 F.
Applications
There are several applications of Information Theory in Digital Communications:
1. Data Compression: It guides the development of efficient compression algorithms, enabling data reduction while preserving essential information.
2. Error-Correcting Codes: Error-correcting codes were developed as a solution of information theory, guaranteeing dependable data transfer over noisy channels.
3. Channel Capacity: It determines the maximum data rate that can be transmitted over a channel, optimizing communication system design.
4. Modulation and Coding: Information theory informs the selection of modulation and coding schemes, balancing data rate, power efficiency, and error resilience.
5. Cryptography: Information theory underlies cryptographic techniques, securing data transmission and protecting against unauthorized access.
6. Network Information Theory: Information theory optimizes network performance, enabling efficient data transmission and reception in complex networks.
7. Signal Processing: Information theory enhances signal processing techniques, improving signal quality and reducing noise.
8. Digital Watermarking: Information theory facilitates digital watermarking, allowing for secure and robust embedding of hidden information.
9. Data Hiding: Information theory enables data hiding techniques, concealing information within digital signals.
10. Optical Communications: Information theory improves optical communication systems, maximizing data transmission rates and minimizing errors.
Information theory’s applications in digital communications have revolutionized data transmission, reception, and processing, enabling efficient, reliable, and secure communication systems.
FAQs
1. What is Information Theory?
- Information Theory provides a mathematical foundation for understanding and optimizing how information is measured, stored, and transmitted.
- It provides fundamental limits on data compression, reliable communication over noisy channels, and efficient information transmission.
2. Why is Information Theory important in Digital Communication?
- Information Theory plays a crucial role in digital communication by providing:
- Data compression: Techniques to efficiently encode information using fewer bits.
- Error correction codes: Methods to detect and correct errors introduced during transmission.
- Channel capacity: The theoretical maximum rate at which information can be reliably transmitted over a communication channel.
3. What are the key concepts in Information Theory?
- Entropy: Measures the uncertainty or information content of a message.
- Mutual Information: Quantifies the amount of information shared between two random variables.
- Channel Capacity: The highest rate of reliable information transfer achievable on a given channel.
- Source Coding: The process of efficiently representing information from a source.
- Channel Coding: The process of adding redundancy to data to protect it against errors during transmission.
4. What are some applications of Information Theory in Digital Communication?
- Data Compression: Used in image, audio, and video compression algorithms (e.g., JPEG, MP3, MPEG).
- Error Correction: Applied in communication systems to ensure reliable data transmission over noisy channels.
- Channel Coding: Used in wireless communication systems to improve signal quality and increase data rates.
- Cryptography: Provides the theoretical foundation for secure communication and data encryption.
5. Who is considered the father of Information Theory?
- Claude Shannon is widely regarded as the father of Information Theory. His groundbreaking paper, “A Mathematical Theory of Communication,” laid the foundation for this field in 1948.
