Half Adder in Digital Logic Design

A Half Adder is a basic digital circuit that performs addition on two binary digits (bits).

Digital Computer

Basic Arithmetic Operations

1. ADDER

2. SUBTRACTOR

3. MULTIPLIER

4. COMPARATOR

HALF ADDER

Half Adder is a combination circuit that can add two binary bits.

The number of inputs is 2.

The number of outputs is 2.

Sum-S, carry-C x,y[augend, addend]

The Half Adder adds the two input bits and generates:

– Sum (S): The result of the addition (0 or 1)

– Carry (C): The carry-out bit (0 or 1), which indicates if the result exceeds 1

Truth Table

x	y	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Simplified expression

x’ y’	x’y
xy’	xy

S=xy’+x’y

0	1
1	0

C=xy

0	0
0	1

Realization

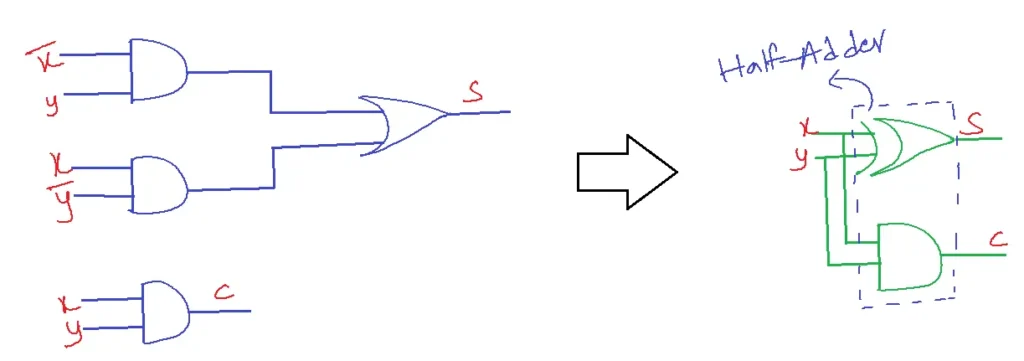
Advantages of Half Adder

1. Simplest adder circuit: It is the most basic adder circuit, making it easy to understand and implement.

2. Fast operation: It operates quickly, as it only requires a single clock cycle to produce the sum and carry outputs.

3. Low power consumption: This adder consumes less power equal to more complex adder circuits.

4. Small size: This Adder requires minimal space, making it ideal for compact digital designs.

5. Basic building block: A basic building block for creating increasingly intricate arithmetic circuits is called a half adder.

Disadvantages of Half Adder

1. Limited functionality: It only performs addition on two single-bit numbers, limiting its applicability.

2. No carry-in input: This Adder doesn’t account for carry-in from previous additions, making it unsuitable for multi-bit additions.

3. Produces incorrect results: When working with multi-bit numbers or when carry-in is necessary, the half-adder yields inaccurate results.

4. Not suitable for large numbers: This Adder is only for small numbers, as it can’t handle large numbers or complex arithmetic operations.

5. Less accurate: This Adder is less precise similar to more advanced adder circuits, like Full Adders or Ripple Carry Adders.

Applications

1. Basic Arithmetic Circuits: Half Adders are building blocks for constructing more complex arithmetic circuits, like Full Adders, Subtractors, and Multipliers.

2. Digital Counters: Half Adders are used in digital counters to increment or decrement counts.

3. Simple Calculators: Half Adders are used in basic calculators for simple arithmetic operations like addition and subtraction.

4. Digital Signal Processing: Half Adders are used in digital signal processing applications, such as audio and image processing.

5. Error Detection and Correction: Half Adders are used in error detection and correction circuits, like parity generators and checkers.

6. Digital Communication Systems: Half Adders are used in digital communication systems for data encoding and decoding.

7. Computer Arithmetic Logic Units (ALUs): Half Adders are used in ALUs to perform basic arithmetic and logical operations.

8. Digital Instrumentation: Half Adders are used in digital instrumentation, like digital multimeters and oscilloscopes.

9. Cryptography: Half Adders are used in cryptographic algorithms, like encryption and decryption.

10. Educational Tools: Half Adders are used as educational instruments to teach digital electronics and computer architecture.

FAQs

1. What is a half-adder in digital logic?

A half adder is a fundamental digital circuit that performs binary addition of two single bits: the augend and the addend.
It produces two outputs: the sum of the two input bits and a carry bit, representing an overflow into the next higher-order bit position.
Half adders are the building blocks for more complex adders in computers and other digital systems.

2. What is the truth table for a half-adder circuit?

The truth table for a half-adder visually represents all possible input combinations and their corresponding outputs. For inputs A and B, the sum (S) and carry (C) outputs are:

A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

This table shows how the half adder generates the sum and carry based on the binary addition rules.

3. How is a half-adder implemented using logic gates?

A half adder can be constructed using one XOR gate (Exclusive OR) for the sum output and one AND gate for the carry output.
The inputs A and B are connected to the XOR and AND gates.
The XOR gate produces a ‘1’ output when only one input is ‘1’, representing the sum bit.
Only when both inputs, which stand for the carry bit, are ‘1’ does the AND gate provide a ‘1’ output.

4. What is the difference between a half and a full adder?

While a half adder adds two single bits, a full adder takes three bits as input: the augend, the addend, and a carry-in from a previous stage.
This allows full adders to be cascaded to perform addition on multi-bit numbers.
A full adder can be built using two half adders and an OR gate.

5. What are the applications of half-adders in digital systems?

The basic building elements of CPUs’ arithmetic logic units (ALUs) are half-adders.
They are also utilized in calculators, address decoders, and other digital circuits requiring binary addition.
While seemingly simple, half-adders play an important part, in enabling complex computations within modern digital systems.

6. How does a half-adder handle carry propagation?

A half-adder itself doesn’t handle carry propagation directly.
It generates a carry output when both inputs are ‘1’, which needs to be passed to the next higher-order bit position for further processing.
This is where full adders, which incorporate a carry-in input, become essential for multi-bit addition.

7. Can a half-adder be implemented using only NAND or NOR gates?

Yes, a half-adder can be implemented using only NAND or NOR gates.
These universal gates can be combined to create any logic function, including the XOR and AND gates required for a half-adder.
This allows for greater flexibility and potential cost savings in circuit design.

8. What are some practical examples of where half-adders are used?

Beyond CPUs and calculators, half-adders are used in various digital systems.
For example, half-adders can contribute to pixel operations like averaging or blending in a digital image processing unit.
Additionally, they’re found in networking hardware for tasks like checksum calculations, ensuring data integrity during transmission.