Gray code is a binary number system where two successive values differ by only one bit. It’s used in digital logic design for:
1. Error detection: Gray code helps detect single-bit errors in data transmission.
2. Encoder and decoder design: Gray code is used in rotary encoders and decoders to track mechanical positions.
3. Digital-to-analog conversion: Gray code is used in digital-to-analog converters (DACs) to reduce errors.
4. Counting and addressing: Gray code is used in counters and address decoders to minimize errors.
Table of Contents
Properties of Gray code
1. Single-bit change: Only one-bit changes between successive values.
2. Cyclic: The final value deviates from the initial value by one bit.
3. Unambiguous: No two values are identical.
| 435 | BCD | 8421 | 84-2-1 | EXCESS 3 |
| 0100 0011 0101 | 0100 0011 1011 | 0100 0101 0111 | 0111 0110 1010 | |
| UNUSED CODES | 10,11,12,13,14,15 | 5,6,7,8,9,10 | 1,2,3,12,13,14 | 0,1,2,13,14,15 |
We can write Gray code for any ‘n’ bit binary number.
Same-0
Different-1
| Decimal | Binary | Grey |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 11101 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 10001 |
| 15 | 1111 | 1000 |
The distance between two successive codes in the gray code is one.
Distance is the number of bits to be changed in one code to get another code is called the distance between the codes.
Gray code for 3-bit:
0-000-000
1-001-001
2-010-011
3-011-010
4-100-110
5-101-111
6-110-101
7-111-100
Advantages of Gray Code
1. Error Detection: This code helps detect single-bit errors in data transmission.
2. Reduced Errors: This code minimizes errors in digital-to-analog conversion and encoder/decoder design.
3. Simplified Design: This code simplifies the design of encoders, decoders, and digital-to-analog converters.
4. Unambiguous: This code ensures an unambiguous representation of values.
5. Cyclic: Grey code’s cyclic nature makes it suitable for rotary encoders and circular addressing.
Disadvantages of Gray Code
1. Complex Conversion: Converting binary code to Grey code and vice versa can be complex.
2. Limited Applications: This code is mainly used in specific applications like encoders, decoders, and DACs.
3. Not Suitable for Arithmetic: This code is not applicable for arithmetic operations due to its non-weighted representation.
4. More Bits Required: This code may require more bits than binary code for the same number of values.
5. Decoding Complexity: Decoding this code can be more complex than decoding binary code.
Applications
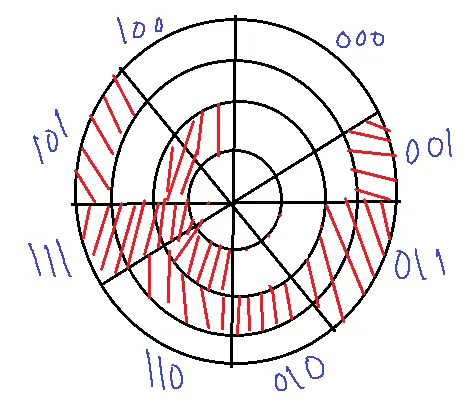
- The important characteristic of this code is each code differs by one code. Successive codes differ by one bit. Use this grey code to determine angular displacement (greater inaccuracy).
- n bits is 2 power n codes. n+1 bits is 2 power n+1 codes. 2n+1=2n.2
- The first 2n codes forwards of n+1 bit grey code equals the forwards of n bit grey code written in order with leading zero dependent.
- The last 2n code forwards of n+1 grey code are equal to the forwards of n bit grey code but written in reverse order with leading one dependent.
- Rotary Encoders: This code minimizes errors in rotary encoders, allowing accurate position readings at high speeds.
- Karnaugh Maps: This code labeling on K-maps simplifies logic minimization by arranging adjacent cells with a single-bit difference, aiding pattern identification and Boolean expression reduction.
- Error Detection & Correction: This code encoding in digital communication aids error detection and correction, reducing multiple-bit errors during transmission for reliable data communication.
- Analog-to-Digital Converters (ADCs): This code sequencing minimizes quantization errors in ADCs by ensuring only one-bit changes during transitions, leading to more accurate digital representations of analog signals.
- Asynchronous FIFOs: This code counters track fill levels in asynchronous FIFOs to prevent metastability issues during transitions, ensuring data integrity.
FAQs
1. What is Gray Code?
- The Gray code also known as reflected binary code, is a binary numeral system where adjacent values differ in only one bit.
- This feature significantly reduces errors in digital systems, especially during numerical transitions.
2. How is Gray Code different from Binary Code?
- The primary difference lies in how consecutive values are represented.
- In binary code, multiple bits can change simultaneously between numbers, leading to potential errors during transitions.
- Gray code ensures only one-bit changes at a time, reducing the likelihood of errors.
3. What are the advantages of using Gray Code?
- Error Reduction: Minimizes errors caused by multiple-bit changes during transitions, crucial in digital communication and analog-to-digital conversion.
- Simplified Hardware: Reduces the complexity of digital circuits that handle transitions between numbers.
- Position Encoding: Used in rotary encoders to accurately represent angular positions with minimal errors.
4. What are the applications of Gray Code?
- Digital Communication: Encoding data for reliable transmission over noisy channels.
- Analog-to-Digital Conversion: Reducing quantization errors during conversion.
- Rotary Encoders: Representing shaft positions in machinery and robotics.
- Karnaugh Maps: Simplifying Boolean function minimization.
- Error Detection and Correction: Detecting and correcting single-bit errors in data transmission.
5. How do you convert between Gray Code and Binary Code?
- Gray to Binary: Follow specific algorithms involving XOR operations and bit shifts.
- Binary to Gray: Employs XOR operations to guarantee single-bit transitions.
