Gauss’s Law states that the total flux passing through any closed surface is comparable to the charge enclosed by that surface.
A closed line gives us an open surface.
A closed surface gives us volume.
Table of Contents
The total flux is given in below figure:
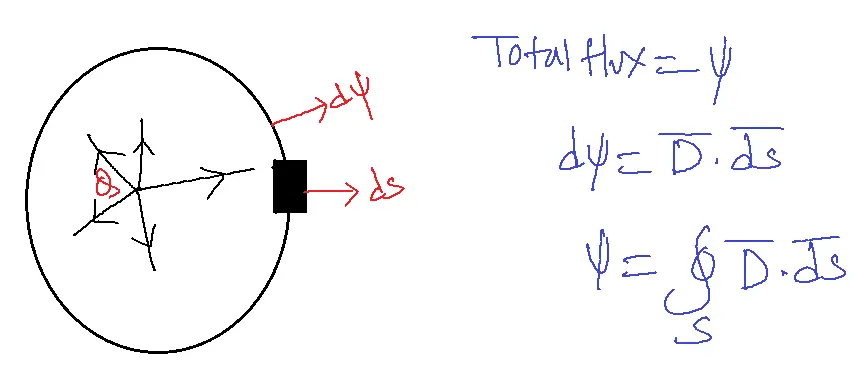
D’=flux density
If flux lines are normal to the surface
D’.ds’= D. ds
If flux lines are tangent to the surface
D’.ds’=0
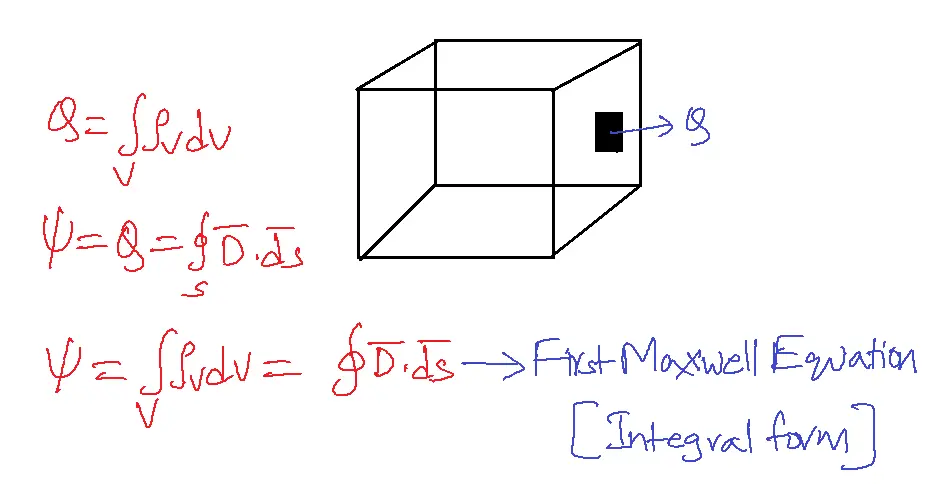
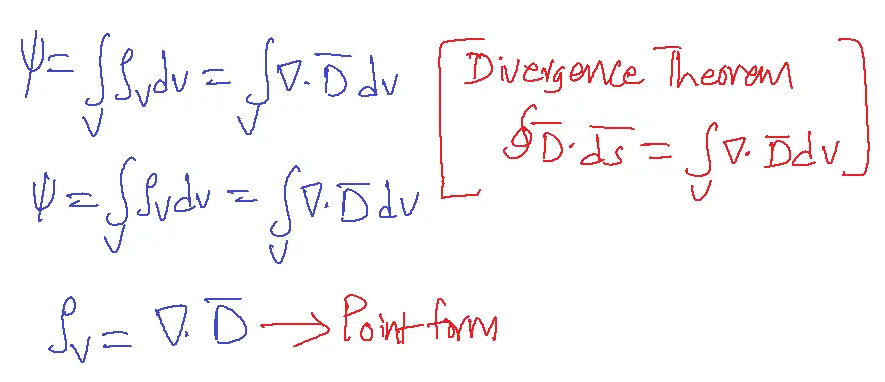
The divergence of electric flux density is the same as volume charge density.
Divergence tells the strength of the source.

Gauss Law can be applied to find electric field intensity if the charge distributions are symmetrical. If the charge distribution is the function of x, y, or z then charge distributions are set to have rectangular symmetry.
Examples:
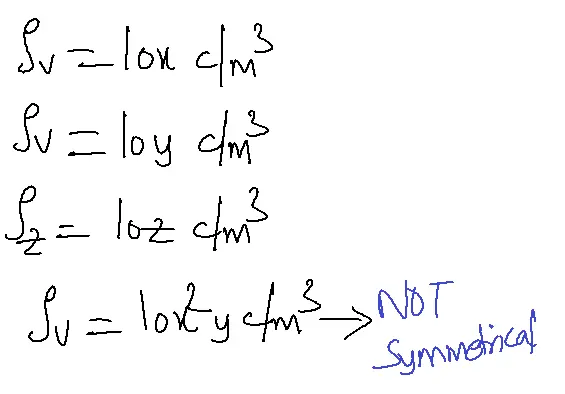
If the charge distribution is the function of only the dow symbol(independent of phi, z), then the charge distribution is set to have cylindrical symmetry. If the charge distribution is the function of a row(independent of theta, phi), then the charge distribution is set to have spherical symmetry.
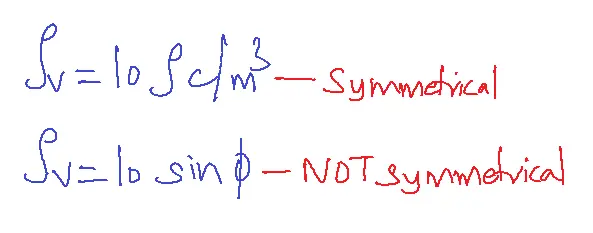
Gauss’s law always holds good even if charge distributions are not symmetrical.
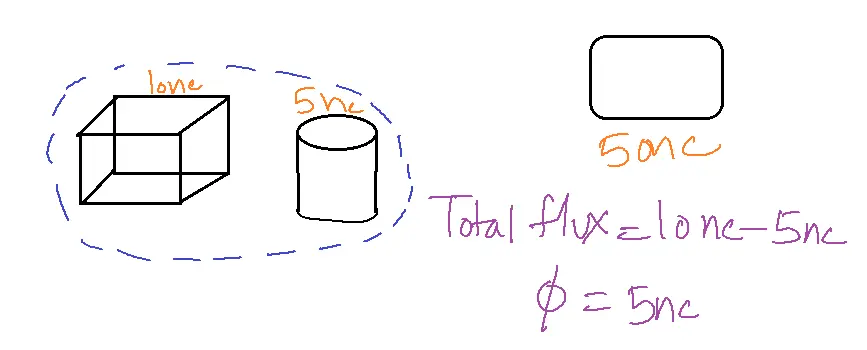
Proper usage of the divergence theorem to Coloumb’s law results in Gauss law.
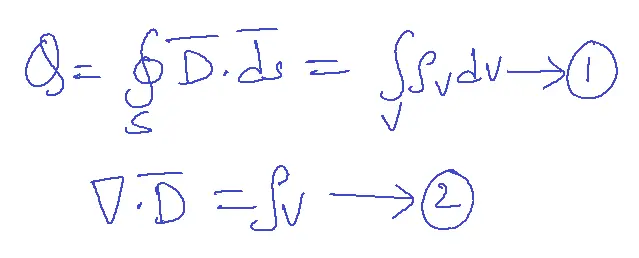
Equations 1 and 2 are two different ways of stating Gauss’s law.
Equation 1 is in integral form.
Equation 2 is in point form.
Gauss’ Law, also known as the Gauss-Ostrogradsky theorem, is a fundamental concept in physics and mathematics that relates the distribution of electric charge to the resulting electric field.
Gauss’ Law has several important implications
1. Electric field lines originate from positive charges and terminate on negative charges.
2. The electric field is proportional to the charge density.
3. The electric field is conservative, meaning it can be expressed as the gradient of a potential function.
Gauss’ Law is a powerful tool for calculating electric fields and solving numerical problems in electrostatics. It is widely used in physics, engineering, and other fields to:
1. Calculate electric fields and potentials
2. Determine charge distributions
3. Analyze electromagnetic phenomena
Gauss’ Law is named after Carl Friedrich Gauss, who first formulated it in the 19th century.
Advantages of Gauss’ Law
1. Simplifies Electric Field Calculations: Gauss’ Law provides a straightforward method for calculating electric fields in symmetric charge distributions.
2. Conservative Nature: Gauss’ Law shows that the electric field is conservative, allowing for the definition of an electric potential.
3. Universal Applicability: Gauss’ Law applies to all charge distributions, making it fundamental in electrostatics.
4. Easy to Apply: Applying Gauss’ Law is easy, particularly in high symmetry scenarios.
5. Powerful Tool for Problem-Solving: Gauss’ Law is a powerful tool for solving problems in electrostatics, allowing for the calculating of electric fields, potentials, and charge distributions.
Disadvantages of Gauss’ Law
1. Limited to Electrostatics: Gauss’ Law only applies to static electric fields, not to fields that change over time or magnetic fields.
2. Requires Symmetry: Gauss’ Law is most useful in circumstances with a high degree of symmetry, making it less applicable to complex charge distributions.
3. Difficult to Apply in Certain Cases: Gauss’ Law can be challenging to compare in cases with non-uniform charge distributions or complex geometries.
4. Does Not Provide Vector Information: Gauss’ Law only provides the magnitude of the electric field, not its direction.
5. Not Directly Applicable to Moving Charges: Gauss’ Law is not directly applicable to moving charges, requiring more advanced techniques like the Lorentz force equation.
Applications of Gauss Law
-check for symmetry
-construct a mathematical closed surface around the charge and assume it as a Gaussian surface.
-Think of the electric flux density D as a tangent to the surface or as a normal to the surface.
-If it is normal D’.ds’=D.ds
-If it is tangential D’.ds’=0.
Gauss’ Law has numerous applications in:
1. Electric Field Calculations: Calculate electric fields in various charge distributions, such as point charges, lines, and surfaces.
2. Electrostatic Potential: Calculate electrostatic potentials and voltage differences between points.
3. Capacitance Calculations: Calculate the capacitance of various capacitors, including parallel plate, spherical, and cylindrical capacitors.
4. Electric Flux Calculations: Calculate electric flux through surfaces, which is essential in understanding electromagnetic induction.
5. Magnetic Field Calculations: Gauss’ Law for magnetism helps calculate magnetic fields and flux.
6. Electromagnetic Induction: Understand electromagnetic induction, Faraday’s law, and Lenz’s law.
7. Electrostatic Shielding: Design electrostatic shields to enclose or exclude electric fields.
8. Bioelectricity: Understand the behavior of electric fields in biological systems, such as nerve conduction.
9. Electrostatic Precipitation: Design electrostatic precipitators to remove pollutants from gases.
10. Particle Accelerators: Understand the behavior of charged particles in electromagnetic fields.
11. Electromagnetic Waves: Understand the behavior of electromagnetic waves, including light, radio waves, and X-rays.
12. Electronics: Design and analyze electronic devices, such as capacitors, resistors, and inductors.
FAQs
1. What is Gauss’s Law?
- Gauss’s Law states that the total electric flux through any closed surface is directly proportional to the net electric charge enclosed by the surface. In simpler terms, it relates the electric field to the charge distribution that creates it.
2. What is the mathematical expression of Gauss’s Law?
- The mathematical expression of Gauss’s Law is
∮ E • dA = Q_enclosed / ε₀
- Where:
- ∮ E • dA is the surface integral of the electric field over a closed surface.
- Q_enclosed is the total charge enclosed by the surface.
- ε₀ is the permittivity of free space.
3. What are the applications of Gauss’s Law in EMTL?
- Gauss’s Law is a powerful tool for calculating electric fields in situations with symmetrical charge distributions. It simplifies the calculation of electric fields in cases like:
- Point charges
- Infinite lines of charge
- Infinite planes of charge
- Spherical shells of charge
4. What are the limitations of Gauss’s Law?
- Gauss’s Law is most useful for symmetrical charge distributions. Complex or asymmetrical charge distributions present a challenge in identifying an appropriate Gaussian surface for a straightforward application of Gauss’s law.
- Gauss’s Law only provides information about the electric field. It doesn’t directly give information about the potential or other electromagnetic quantities.
5. How is Gauss’s Law related to Coulomb’s Law?
- Gauss’s Law and Coulomb’s Law are closely related. Gauss’s Law can be derived from Coulomb’s Law, and vice-versa. Coulomb’s Law describes the force between two point charges, while Gauss’s Law provides a more general relationship between electric field and charge distribution.
