Gain Margin (GM) and Phase Margin (PM) are measures of a control system’s stability and robustness.
Stability Analysis
- Gain cross-over frequency: Gain cross-over frequency is defined as the frequency at which the gain is one or the magnitude of the increase is 0 dB. The bode plot barely crosses the 0dB line at the gain cross-over frequency.
- Phase cross-over frequency: It is a frequency at which the angle is -1800.
Importance of Gain Margin and Phase Margin
1. Stability: GM and PM ensure system stability and prevent oscillations.
2. Robustness: GM and PM ensure system robustness to parameter variations and disturbances.
3. Performance: GM and PM impact system performance, such as response time and overshoot.
Table of Contents
Gain Margin(GM)
- The gain margin is the gain increase required to make the system unstable.
- Units are measured in dB.
- A higher GM indicates a more stable system, as it can tolerate more gain increases before becoming unstable.
- A GM of 10-20 dB is considered good.
- GM in dB=-20 log[|Gjw+(jw)|]
- For a stable system, GM and PM must be positive.
- A system with zero gain and PMs is considered marginally stable.
- A negative gain or PM indicates system instability.
Procedure to Calculate Gain Margin
1. Determine phase cross-over frequency by equating the imaginary part of the given transfer function to zero. it is the frequency at which the phase equals -180 degrees.
2. Determine the magnitude at w=wPc.
3. GM=1/A.
4. GM in dB=20 log [1/A]
5. If it is positive, the system is stable. If it is negative, the system is unstable. If it is 0, the system is marginally stable.
Example
The open loop transfer function of a system G(s)=1/s(s+1)(s+2). Determine gain margin (GM).
Solution: s=jw
1/jw(jw+1)(jw+2)

A=1/6
GM=1/A=6.
20 = 15.5 dB.
The GM is positive, the system is stable.
A=1/6
GM=1/A=6.
20 = 15.5 dB.
The GM is positive, the system is stable.
Advantages
- Ensures System Stability: The primary advantage of this margin is its direct link to system stability. A positive GM indicates that the system can tolerate some increase in gain without oscillating or becoming unstable.
- Predicts Robustness to Parameter Variations: It ensures stable system operation despite parameter variations.
- Facilitates Controller Design: When designing controllers, engineers aim to optimize performance while ensuring stability. It is crucial for tuning controller gains and meeting stability requirements.
- Simplifies System Analysis: By examining the GM, engineers can quickly assess the stability of a system without performing complex mathematical calculations. This simplifies the analysis process and aids in understanding the system’s behavior.
- Enhances System Reliability: A system with a good GM is less likely to experience unexpected instability due to external disturbances or component failures. This increased robustness translates to improved system reliability and reduced downtime.
Disadvantages
- Limited Stability Indicator: GM alone is insufficient to assess system stability. It overlooks potential instability beyond the phase crossover frequency.
- Neglects Phase Information: It ignores phase response, leading to potential instability despite a high GM.
- Sensitivity to Parameter Variations: It can be sensitive to changes in system parameters. Even minor variations in component values or operating conditions can significantly impact the GM and potentially lead to instability.
- Doesn’t Guarantee Transient Response: While it helps assess stability, it doesn’t guarantee a desirable transient response. A system with a large GM may still exhibit excessive overshoot or oscillations in its response to disturbances.
- Inapplicable to Non-Linear Systems: It is primarily used for linear systems. It may not apply directly to non-linear systems where the behavior is more complex and depends on the input signal amplitude.
Applications
1. Controller Design: GM guides the selection of appropriate controllers, such as PID controllers, to ensure stable operation.
2. Stability Analysis: GM predicts oscillations and instability, enabling corrective actions to be taken.
3. Robustness Evaluation: GM evaluates system robustness to parameter variations and disturbances.
4. Performance Optimization: GM optimizes system performance, balancing response time and overshoot.
5. Aerospace Engineering: GM contributes to the reliable and safe operation of aircraft and spacecraft control systems.
Phase Margin(PM)
- The phase margin is the phase shift required to make the system unstable.
- Its units are degrees.
- A higher PM indicates a more stable system as it can tolerate more phase shifts before becoming unstable.
- A PM of 30-60 degrees is considered good.
- Increasing GM often reduces PM, and vice versa.
- A balance between GM and PM is sought for optimal system performance.
Procedure to calculate phase margin
1. Determine gain cross-over frequency by equating the magnitude of the given transfer function to 1.
2. Calculate phase at w= wgc
3. PM=1800+phi(wgc)
4. When it is positive, the system is stable. When it is negative, the system is unstable. When it is 0, the system is marginally stable.
Example
The open loop transfer function of a system G(s)=5/s(1+0.01s). Determine phase margin.
Solution:
S=jw
5/jw(1+0.01jw)
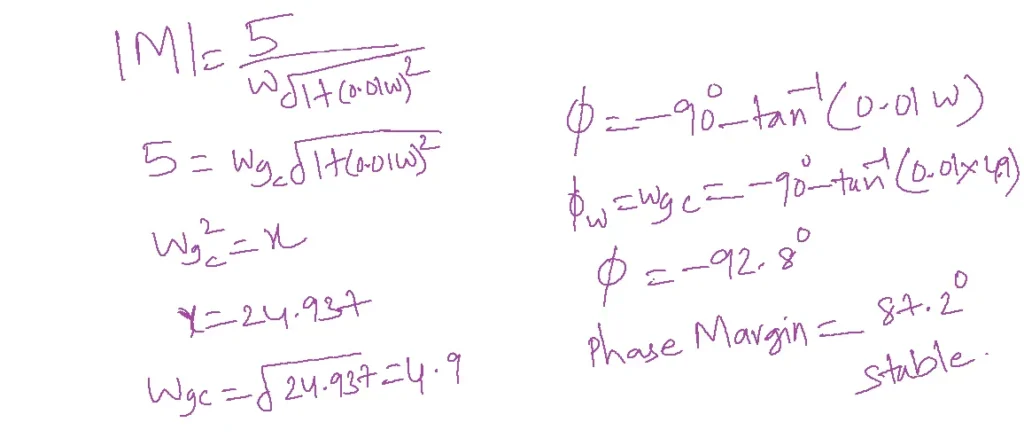
Advantages
- Ensures System Stability: It is a key indicator of a control system’s stability. A positive PM guarantees the system will not oscillate or exhibit undesirable behavior, ensuring reliable and predictable operation.
- Predicts Transient Response: Higher PMs generally translate to better transient responses with less overshoot and faster settling time. This is crucial for achieving the desired system performance and minimizing oscillations during disturbances.
- Provides Robustness against Parameter Variations: A healthy PM offers stability despite parameter changes.
- Enables Aggressive Control Designs: Systems with higher PMs can accommodate more aggressive controller designs, leading to faster response times and improved performance without sacrificing stability.
- Simplifies Controller Tuning: Understanding this margin helps engineers fine-tune controller parameters to achieve the desired balance between stability and performance. It simplifies the design process and reduces the risk of instability.
Disadvantages
- Limited Stability Indicator: It alone doesn’t guarantee complete system stability. It only considers the phase at the gain crossover frequency and may overlook potential instability at other frequencies.
- Neglects Gain Information: It primarily focuses on the phase response and doesn’t account for the system’s gain. A system with a large PM might still be unstable if the gain is excessively high.
- Sensitivity to Parameter Variations: It can be sensitive to changes in system parameters. Even minor variations in component values or operating conditions can significantly impact the PM and potentially lead to instability.
- Doesn’t Guarantee Transient Response: While it helps assess stability, it doesn’t provide a complete picture of the system’s transient response. A system with a large phase margin may still exhibit undesirable overshoots or oscillations in response to disturbances.
- Inapplicable to Non-Linear Systems: It is primarily used for analyzing linear systems. Its direct application to non-linear systems, where the behavior is more complex and depends on the input signal amplitude, is limited.
Applications
1. Process Control: In industries like chemical processing, oil refining, and power generation, PM plays a vital role in maintaining safe and efficient processes.
2. Automotive Systems: PM ensures stable operation in vehicle control systems, like cruise and traction control.
3. Robotics: PM ensures stable and precise movement in robotic control systems.
4. Power Systems: PM actively safeguards against blackouts by maintaining power grid stability through effective control and analysis.
5. Research and Development: PM aids in developing new control systems and algorithms in academic and research settings.
FAQs of Related Topic
1. What are phase margin and gain margin in a control system?
- Phase and gain margins are essential stability criteria in control systems.
- Phase margin is the additional phase lag a system can handle at the gain crossover frequency before it becomes unstable.
- The gain margin is the additional gain a system can tolerate at the phase crossover frequency before it becomes unstable.
2. Why are phase margin and gain margin important?
- They help ensure the stability and robustness of a control system.
- Positive phase and gain margins ensure system stability against parameter variations and external disturbances.
3. How are phase margin and gain margin calculated?
- Both are calculated from the Bode plot of the open-loop transfer function.
- Phase margin: PM is the angular difference between the system’s phase response at the gain crossover frequency and -180 degrees.
- Gain margin: It is the inverse of the gain (in dB) at the phase crossover frequency (where the phase is -180 degrees).
4. What are considered good values for phase margin and gain margin?
- In the realm of control system design, a phase margin falling between 45 and 60 degrees, coupled with a GM of 6 to 12 dB, is commonly accepted as indicative of a robust and stable system.
- However, specific applications may require different values depending on the desired performance and robustness.
5. How can phase margin and gain margin be improved in a control system?
- Various techniques can be used, including:
- Controller tuning: Adjusting the Controller gains (e.g., PID gains) can influence both margins.
- Compensation: Adding lead or lag compensators can reshape the frequency response to improve stability margins.
- Reducing system gain: Lowering the overall system gain can sometimes improve both phase and gain margins.
