A key idea in physics and engineering continuity equation characterizes how mass or charge is conserved in a system. It states that the rate of change of charge or mass in a system is equal to the difference between the rate at which it flows into the system and the rate at which it flows out.
In simpler terms, the continuity equation says that:
- The rate of change of charge or mass in a system (left side of the equation)
- It is equal to the difference between:
- The rate at which charge or mass flows into the system (positive contribution)
- The rate at which charge or mass flows out of the system (negative contribution)
Table of Contents
Generation and Recombination
In a pure semiconductor, the number of holes is comparable to the number of free electrons. Due to thermal agitation new electron hole pairs are generated. Simultaneously the other hole electron pairs disappear, as a result of recombination. i.e., free electrons falling into empty covalent bonds.
On average a hole exists per Tow P seconds known as the mean lifetime of holes. Similarly, an electron exists for Tow n seconds known as the mean lifetime of electrons.
Carrier Lifetime
The definition of this is the amount of time a charge carrier will remain before recombining with a charge carrier of the opposing charge. Its value varies from nanoseconds to hundreds of microseconds and depends on the temperature and impurity concentration in the semiconductor material.
Continuity Equation Derivation
The carrier concentration in the body of the semiconductor is the function of time and distance. Mathematically a partial differential equation governs this functional relation between carrier concentration, time and distance is the continuity equation. The idea behind the continuity equation is that a charge can never be generated or destroyed.
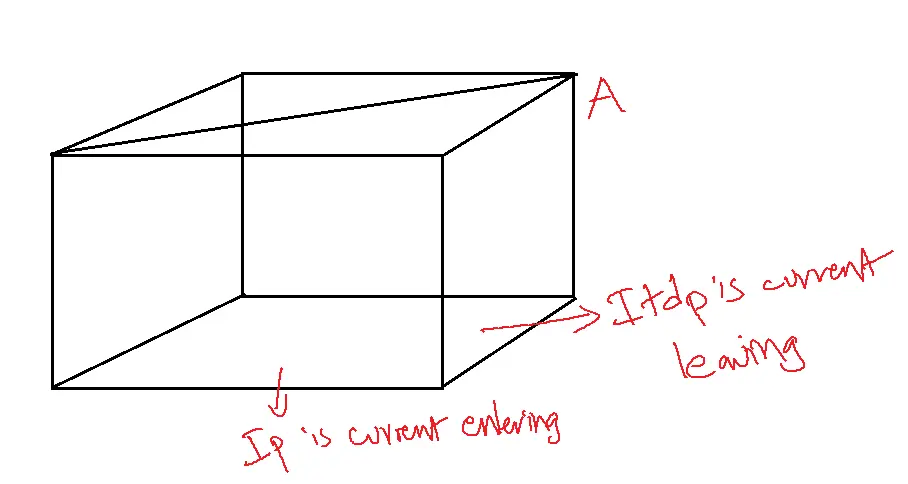
Consider a tiny element of A and the length is dx.
Let p be the hole concentration within this volume.
The current entering the volume at x is Ip and leaving at x+dx is I+dIp.
The change in current is because of diffusion.
Due to diffusion, the concentration of charge carriers decreases exponentially with distance(dIp).
If Tp is the mean lifetime of the hole then the holes lost per second due to recombining per volume is equal to
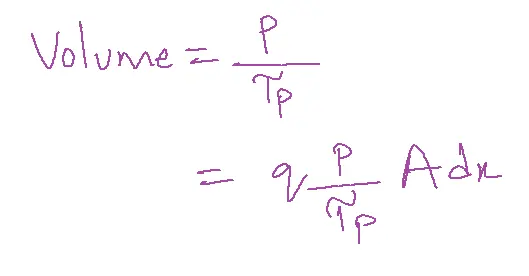
Let g be the rate at which electron-hole pairs are generated
Columbus per second are generated within this volume=qgAdx
Total change in current (c/sec) = q (dp/dt) A dx
But According to the law of conservation of charge
q (dp/dt) A dx = -q P/T(tow) A dx + qgAdx – dIp.
J=I/A
dJ=dI/A
dI = A dJ
once the semi-conductor comes to equilibrium
dp/dt=0
No external electric field P=Po
g=Po/T(Tow)
Diffusion current J= -qDpdp/dx+qDpPE
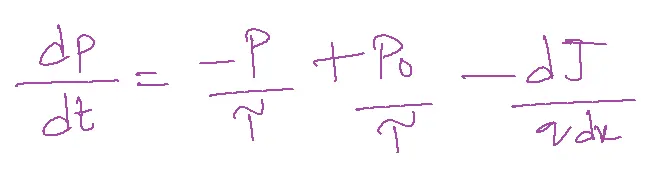

In n-type:
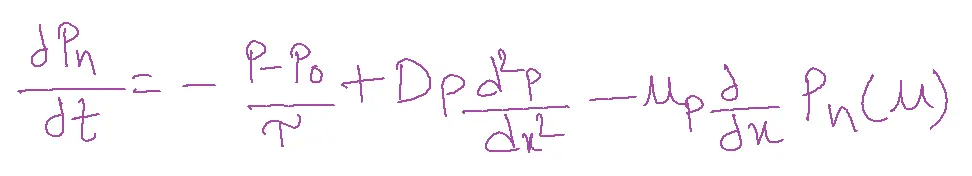
In p-type
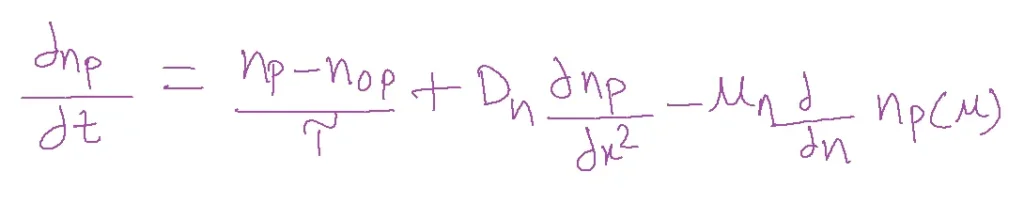
Applications of Continuity Equation
1. Electric Circuits: Ensures charge conservation, helping design and analyze circuits.
2. Fluid Dynamics: Ensures mass conservation, key for understanding fluid flow, pressure, and velocity.
3. Semiconductor Devices: Ensures charge carrier (electrons and holes) conservation, vital for designing and analyzing diodes, transistors, and solar cells.
4. Thermodynamics: Helps analyze heat transfer and energy conservation.
5. Quantum Mechanics: Used to guarantee probability conservation by describing the particle’s probability density.
6. Plasma Physics: Ensures charge conservation in plasma behavior analysis.
7. Optics: Helps analyze light intensity and energy conservation.
8. Acoustics: Ensures mass conservation in sound wave propagation.
9. Chemical Engineering: Ensures mass conservation in chemical reactions and transport processes.
10. Biological Systems: Helps model and analyze biological processes, like blood flow and nutrient transport.
FAQs
1. What is the Continuity Equation in EDC?
- The Continuity Equation, a cornerstone of electrodynamics, expresses the principle of charge conservation in closed systems.
- It states that the change in charge density within a volume is directly related to the net current entering or leaving that volume.
2. How is the Continuity Equation derived in EDC?
- The Continuity Equation is derived by applying Gauss’s law to a closed surface enclosing a volume.
- The law states that the flux of the electric field through the surface is proportional to the enclosed charge.
- By considering the current flow and charge density within the volume, we can obtain the differential form of the Continuity Equation.
3. What is the significance of the Continuity Equation in EDC?
- The Continuity Equation is essential for analyzing and understanding the behavior of charge carriers in semiconductor devices.
- This equation is instrumental in explaining critical semiconductor phenomena – current flow, carrier diffusion, and recombination – essential for effective electronic device design and modeling.
4. What is the differential form of the Continuity Equation?
- The differential form of the Continuity Equation is:
∂ρ/∂t + ∇ · J = 0
- Where:
- ρ is the charge density
- t is time
- J is the current density
- ∇ · J is the divergence of the current density
5. How is the Continuity Equation applied in semiconductor device analysis?
- The Continuity Equation is applied in various ways in semiconductor device analysis, including:
- Modeling carrier transport: It helps describe how charge carriers move within a semiconductor under the influence of electric fields and concentration gradients.
- Calculating current densities: The equation enables the calculation of current densities within various regions of a semiconductor device.
- Analyzing device behavior: It aids in understanding the operation of devices like diodes, transistors, and solar cells by relating charge carrier distributions to current flow.
