Biot-Savart Law and Ampere’s Circuital Law are important laws that govern the Magneto Static field.
Magneto Static Field (Static Magnetic Field)
H, r, and B characterise the magnetostatic field.
H – Magnetic Field Intensity.
B – Magnetic Flux Density.
The units of H are A/m.
The units of B are wb/m2.
E and D are related by epsilon.
B and H are related by µ.
D = permittivity of medium.
B = µH µ – permeability.
If the charges are moving with constant velocity a static magnetic field is produced, which means DC is generated in the static magnetic field.
Two important laws govern the magnetostatic field.
1. Biot Savart’s Law
2. Ampere’s Circuit Law
Biot Savart’s law is similar to Coloumb’s law which is the general law of the magnetostatic field.
Applications of Static Magnetic Field
The principle of Static Magnetic Field is used in motors, transformers, microphones, computers, telephone bell ringers, +V focussing control, advertising displays, magnetically limited vehicles, memory storage, and magnetic separators.
Table of Contents
Biot-Savart Law
Biot Savart Law states that differential magnetic field intensity dH produced at a point P by the differential current Idl is proportional to the product Idl and the sine of the angle between the element and the line joining P to the element and is inversely proportional to the square of the distance between P and element.

dH α Idlsinα/R2
dH = K Idlsinα/R2
= Idlsinα/4πR2
dH’=Idl’ x aR’/4πR2
dl’ x aR’ = dl.ar’sinα = dlsinα
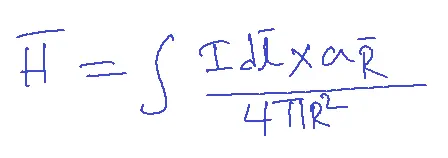
The right-hand thumb rule can be used to identify H’s direction. The thumb points in the direction of the current and the right-hand fingers cycle the wire in the direction of H.
X in the circle indicates magnetic field H into the board.
. in the circle indicates magnetic field H outside the board.

Different current distribution
Line Current:

Surface Current:

Volume Current:
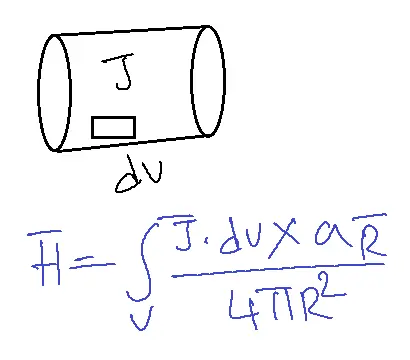
| Current Distribution | Units |
| Line Current I | Amperes A |
| Surface Current K | Ampere per metre A/m |
| Volume current J | Ampere per square metre A/m2 |
| Current Element | Ampere metre Am |
Advantages of Biot-Savart Law
1. Accurate calculations: Biot-Savart’s Law allows for precise calculations of magnetic fields around current-carrying wires and loops.
2. Simplifies complex problems: It simplifies complex magnetic field calculations by breaking them into smaller, manageable parts.
3. Wide applicability: The law applies to various situations, including straight wires, loops, and coils.
4. Easy to use: Biot-Savart’s Law is relatively simple, especially for symmetrical configurations.
5. Fundamental understanding: It provides a fundamental relationship between current and magnetic field.
Disadvantages of Biot-Savart Law
1. Limited to steady currents: The law only applies to steady (direct) currents, not alternating currents (AC).
2. Assumes infinitesimal elements: The law assumes infinitesimally small current elements, which can lead to inaccuracies in certain situations.
3. Difficult to apply to complex geometries: Biot-Savart’s Law can be challenging to apply to complex wire configurations or non-uniform currents.
4. Does not account for magnetic materials: The law assumes a vacuum or air, neglecting the effects of magnetic materials.
5. Not directly applicable to closed loops: Biot-Savart’s Law requires modifications or additional steps to handle closed loops or coils.
Applications of Biot-Savart Law
1. Magnetic Field Calculations: Calculates magnetic fields around current-carrying wires, loops, and coils.
2. Electric Motor Design: Helps design and enhance electric motors, generators, and transformers.
3. Magnetic Resonance Imaging (MRI): Used in MRI machine design to create strong, uniform magnetic fields.
4. Electromagnets: Designs and enhances electromagnets for lifting, holding, and moving heavy metal objects.
5. Magnetic Sensors and Actuators: Develop magnetic sensors and actuators for applications like position sensing, current measurement, and control systems.
6. Wireless Charging Systems: Optimizes wireless charging coils for efficient energy transfer.
7. Particle Accelerators: Calculates magnetic fields for particle steering and focusing in particle accelerators.
8. Magnetic Shielding: Designs magnetic shielding materials and configurations to block or redirect magnetic fields.
9. Geophysical Surveys: Analyzes magnetic fields to understand Earth’s subsurface structure and mineral deposits.
10. Electromagnetic Compatibility (EMC): Ensures electromagnetic compatibility between electronic devices and systems.
Ampere’s Circuital Law

Ampere’s circuital law states that the line integral of the tangential component of magnetic field intensity around a closed path is comparable to the current enclosed by a path.
Apply stokes theorem

The magnetostatic field is not conservative.
The electrostatic field is conservative.
Applications for Ampere’s Circuital Law
1. Infinite line current: Magnetic Field Intensity due to infinite line current using Ampere’s Circuital Law.
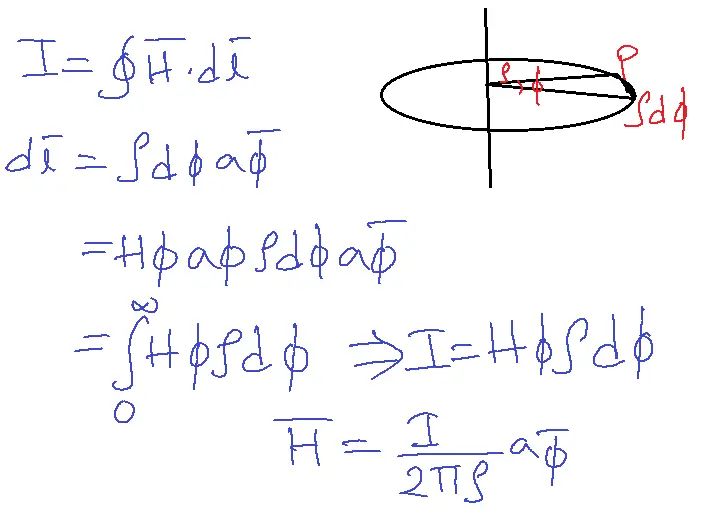
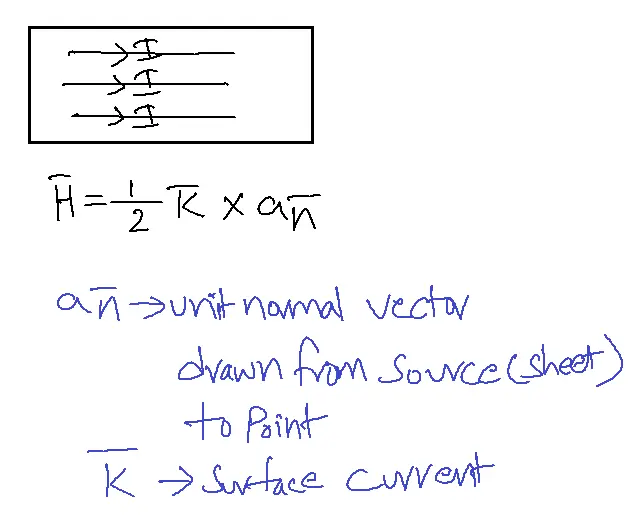
2. Infinite sheet of current
3. Infinite long coaxial line.
Advantages of Ampere’s Circuital Law
1. Simplifies complex calculations: Ampere’s Circuital Law simplifies calculations of magnetic fields around a closed loop.
2. Easy to apply: The law is straightforward, especially for symmetrical configurations.
3. Relates current and magnetic field: Ampere’s Circuital Law establishes a direct relationship between current and magnetic field.
4. Wide applicability: The law applies to various situations, including straight wires, loops, and coils.
5. Fundamental understanding: A basic grasp of the connection between current and magnetic field may be obtained from Ampere’s Law.
Disadvantages of Ampere’s Circuital Law
1. Limited to closed loops: Ampere’s Circuital Law only applies to closed loops of wire, not open-ended wires.
2. Assumes uniform current density: The uniform current density assumed by the law may not always hold.
3. Difficult to apply to complex geometries: Ampere’s Law can be challenging to apply to complex wire configurations or non-uniform currents.
4. Does not account for magnetic materials: The law assumes a vacuum or air, neglecting the effects of magnetic materials.
5. Not directly applicable to time-varying currents: Ampere’s Law requires modifications or additional steps to handle time-varying currents.
Applications of Ampere’s Circuital Law
1. Electric Motor Design: Helps design and enhance electric motors, generators, and transformers.
2. Magnetic Field Calculations: Calculates magnetic fields around closed loops of wire, such as solenoids and toroids.
3. Electromagnets: Designs and enhances electromagnets for lifting, holding, and moving heavy metal objects.
4. Magnetic Sensors and Actuators: Develop magnetic sensors and actuators for applications like position sensing, current measurement, and control systems.
5. Wireless Charging Systems: Optimizes wireless charging coils for efficient energy transfer.
6. Particle Accelerators: Calculates magnetic fields for particle steering and focusing in particle accelerators.
7. Magnetic Resonance Imaging (MRI): Used in MRI machine design to create strong, uniform magnetic fields.
8. Electric Generators and Transformers: Helps design and optimise electric generators and transformers.
9. Magnetic Shielding: Designs magnetic shielding materials and configurations to block or redirect magnetic fields.
10. Electromagnetic Compatibility (EMC): Ensures electromagnetic compatibility between electronic devices and systems.
FAQs
1. What is Ampere’s Circuital Law?
- Ampère’s Circuital Law asserts that the line integral of the magnetic flux density (B) encircling a closed loop is proportional to the product of the permeability of free space (μ₀) and the aggregate current enclosed by the loop.
- This fundamental principle in electromagnetism facilitates the computation of magnetic fields produced by steady currents.
2. What is the Biot-Savart Law?
- The Biot-Savart Law elucidates the magnetic field generated by a current-carrying wire at a specific location in space.
- It posits that the magnetic field at a point is directly proportional to the current, the length of the wire segment, and the sine of the angle between the wire segment and the line connecting the point to the wire segment.
3. What are the differences between Ampere’s Circuital Law and the Biot-Savart Law?
- Ampere’s Circuital Law: We use this law to find the magnetic field produced when a steady current is confined within a closed path.
- Biot-Savart Law: Biot-Savart’s law determines the magnetic field generated at a point by a small current-carrying segment in a wire.
- When dealing with problems exhibiting high symmetry, Ampere’s Law typically offers a more direct and efficient solution.
- For complex current distributions, however, the Biot-Savart Law offers greater flexibility in analysis.
4. What are the applications of Ampere’s Circuital Law?
- Determination of the magnetic field within a solenoid or toroid.
- Evaluation of the magnetic field surrounding a long, rectilinear current-carrying conductor.
- Analysis of the magnetic field generated by a current sheet.
5. What are the applications of the Biot-Savart Law?
- Computation of the magnetic field at a specified point resulting from a current loop.
- Determination of the magnetic field generated by a curved wire.
- Analysis of the magnetic field produced by a complex distribution of current.
