The two symbols used to illustrate letters, numbers, and other data in binary code are 0 and 1. This is the most basic form of computer language, used by computers to understand and process information.
How does binary code work?
1. Text representation: Each character (letter, number, or symbol) is assigned a unique binary code. For example, the letter “A” might be represented as 01100001.
2. Number representation: Numbers are represented in binary using a series of bits. For example, the number 12 might be denoted as 1100.
3. Instruction representation: Computer instructions, like “add” or “jump,” are also represented in binary.
Table of Contents
Classification of Binary Code
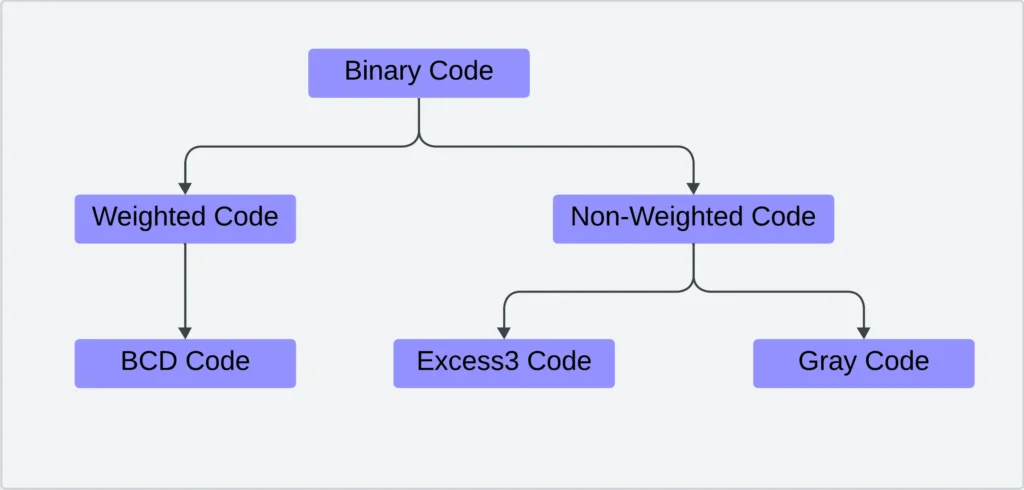
It is of two types:
1. Weighted code– If a particular weight can be assigned to get its corresponding decimal value.
2. Non-weighted code– excess 3 code and gray code are examples
Binary Code – Operation
Binary coded Decimal codes are from 0-9.
In this code, each decimal digit is coded into a 4-bit binary.
For example 1-0001
2-0010
3-0011
Binary code and BCD code are the same up to 9. They are different after 10.
One feature of binary coding is that you may get the code for a decimal number’s 9th complement by converting 1 to 0 and 0 to 1.
Example: 75
Solution: (1001011)2
=(01110101)BCD
8421-self complementary code
0-0000
1-0111
2-0110
3-0101
4-0100
5-1011
6-1010
7-1001
8-1000
9-1111
It has a property that the code for 9’s complement of a decimal number can be obtained by changing 1’s to 0’s and 0’s to 1’s.
| 2 | 4 | 2 | 1 | Excess 3 code | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 6 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 7 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 8 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Advantages of Binary Code
1. Simple and Efficient: It is easy for computers to understand and process.
2. Universal Language: All computers use this code, making it a universal language.
3. Error Detection: It allows error detection and correction.
4. Fast Processing: It enables fast processing and execution of instructions.
5. Low Power Consumption: Compared to other number systems, this code requires fewer processing resources to operate in digital electronics.
6. Easy Storage: It is easy to store and retrieve from memory.
Disadvantages of Binary Code
1. Difficult for Humans: This code is difficult for humans to read and write.
2. Limited Information Density: This code requires more digits to represent information to other number systems.
3. Time-Consuming: Writing and debugging this code can be time-consuming.
4. Prone to Errors: This code is prone to errors, which can be difficult to detect and correct.
5. Not Intuitive: This code is not intuitive, making it challenging for beginners to learn.
6. Dependent on Hardware: This code is dependable on hardware architecture, making it less portable.
Applications
- Data Representation and Storage: It is a fundamental way for digital systems to represent and store information using ‘0’ and ‘1’, enabling efficient processing and storage in computers.
- Logic Gate Operations: Digital logic circuits use this code for logical operations, the foundation of digital computing.
- Instruction Execution: In microprocessors, it represents instructions that control operations and data manipulation.
- Communication Protocols: These codes facilitate data transmission in communication protocols, ensuring accurate information exchange across networks.
- Digital Signal Processing (DSP): This code facilitates efficient filtering, modulation, compression, and other operations on digital data in DSP applications.
FAQs
1. What is binary code?
- Binary code is a system of representing information using only two symbols, typically 0 and 1.
- It’s the fundamental language of digital systems, enabling the representation of numbers, letters, and other data.
2. Why is binary code used in digital logic design?
- This code is used in digital logic design because it directly corresponds to the two voltage levels (high and low) used in electronic circuits.
- This makes it ideal for representing and processing information within digital systems.
3. How is binary code used to represent numbers?
- Binary code uses a positional notation system, where each digit’s position represents a power of two.
- For example, the binary number 1011 represents (1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (1 * 2^0), which equals the decimal number 11.
4. What are some common binary codes used in digital systems?
- Several binary codes are used for different purposes, including:
- BCD (Binary-Coded Decimal): Encodes decimal digits 0-9 with four bits.
- ASCII (American Standard Code for Information Interchange): Represents characters, numbers, and symbols using seven or eight bits.
- Gray code: A specialized code designed for encoders and digital communication, where only a single bit changes between successive numbers.
5. How is binary code used in logic gates and circuits?
- Logic gates, the basic building blocks of digital circuits, operate on binary inputs (0 or 1) to produce binary outputs.
- Complex digital circuits, capable of performing diverse operations like arithmetic, data storage, and decision-making, are built by combining logic gates.
