Binary Addition and Hexadecimal Addition are important operations of number systems in Digital Logic Design and digital electronics.
Table of Contents
Binary Addition
Binary addition in digital logic design is adding two or more binary numbers (numbers represented in base-2) using logical operations.
Binary Numbers means represent numbers using only 0s and 1s (bits).
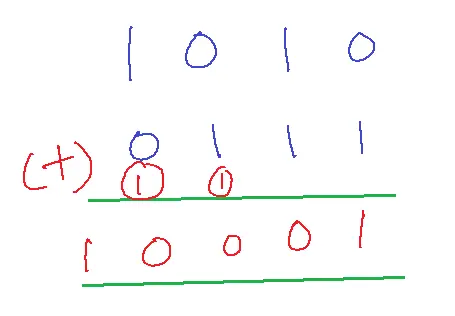
- 0+0=0
- 0+1=1
- 1+0=1
- 1+1=10
If the sum of two bits is 1+1, generate a carry (1) to add to the next higher bit position.
Binary- base 2
Ex: (1110.011)2= 14.37
Solution: 1110= 1 X 23+1 X 22+1X 21+0 X 20
= 14
011=2-1 X 0+ 2-1X 1+ 2-2 X 1
= 0.37
=14.37→ Decimal Number
Applications
1. Computer Arithmetic: Binary addition is the foundation of computer arithmetic, enabling basic operations like addition, subtraction, multiplication, and division.
2. Digital Signal Processing: Binary addition is used in signal processing techniques like filtering, convolution, and Fourier transforms.
3. Cryptography: Binary addition is used in encryption algorithms like AES and RSA to ensure secure data transmission.
4. Error-Correcting Codes: Binary addition is used in error-correcting codes like Hamming code and checksums to detect and correct errors.
5. Digital Logic Design: Binary addition is used in designing digital logic circuits, such as adders, subtractors, and arithmetic logic units (ALUs).
6. Microprocessors: Binary addition is a fundamental operation in microprocessors, enabling instruction execution and data processing.
7. Embedded Systems: Binary addition is used in embedded systems, like traffic light controllers, elevator controllers, and robotic systems.
8. Scientific Computing: Binary addition is used in scientific simulations, like weather forecasting, fluid dynamics, and quantum mechanics.
9. Data Compression: Binary addition is used in data compression algorithms, like Huffman and arithmetic coding.
10. Machine Learning: Binary addition is used in machine learning algorithms, like neural networks and deep learning.
Octal Addition
Octal Addition – Base 8
Example
243.18=(163.2031)–> Decimal Number
243=2 X 82+4 X 81+ 3 X 80
=163
0.18 = 1 X 8-1+ 8 X 8-2
=0.2031
Conversion from Binary Addition to Octal Addition
101010111
Split into three parts from right to left [3-bitpattern]
101-5
010-2
111-7
Hexadecimal Addition
Hexadecimal addition is a way of adding numbers in base-16, using the hexadecimal number system
Hexadecimal- base 16
Example: 137A = 1 X 163+3 X 162+ 7 X 161+ 10 X 160
=(4986)10
4986→ Decimal Number
ECE + EEE = 1DBC
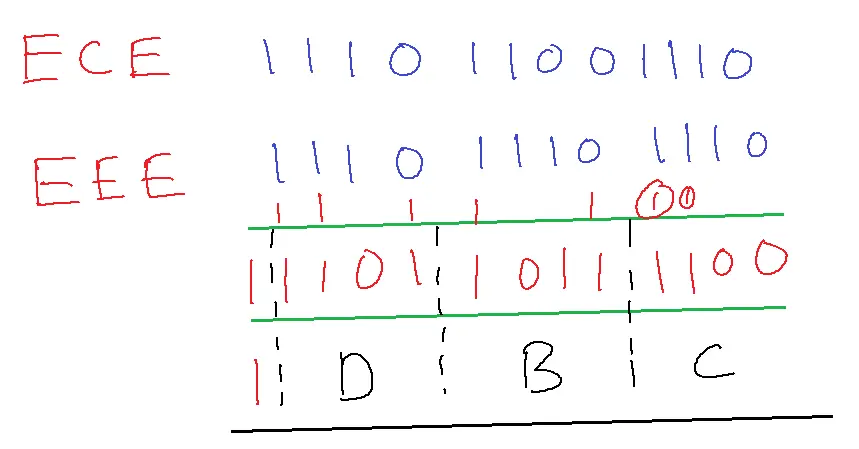
Hexadecimal numbers use 16 distinct symbols: 0-9 (digits) and A to F (letters representing 10-15).
Addition Rules: When adding hexadecimal numbers, follow these rules:
- Add corresponding digits (right to left).
- If the sum is 15 or less, write the result.
- If the sum is 16 or more, subtract 16 and carry 1 to the next digit.
Carry-Over: If the sum of two digits exceeds 15 (F in hexadecimal), subtract 16 and carry 1 to the next digit.
Applications
1. Programming: This addition is used in programming languages like C, C++, and Java for memory addressing, data manipulation, and debugging.
2. Computer Networking: This addition is used in network protocols like TCP/IP, HTTP, and FTP for data transmission and routing.
3. Cryptography: Hexadecimal addition is used in cryptographic algorithms like SSL/TLS, AES, and RSA for secure data encryption and decryption.
4. Data Compression: This is used in data compression algorithms like ZIP, RAR, and GIF for key data storage.
5. Digital Forensics: This is used in digital forensics for analyzing and recovering data from digital devices.
6. Embedded Systems: This is used in embedded systems like traffic light controllers, elevator controllers, and robotic systems.
7. Microcontrollers: This is used in microcontrollers like Arduino and Raspberry Pi for programming and debugging.
8. Web Development: Hexadecimal addition is used in web development for color coding, data encoding, and web security.
9. Database Management: This addition is used in database management systems like MySQL and Oracle for data indexing and retrieval.
10. Computer Graphics: This is used in computer graphics for color manipulation, image processing, and game development.
Representation of Negative numbers
We use complements(negative)
1. r’s complement
2. (r-1)’s complement
In decimal r’s complement is 10’s complement.
In decimal (r-1)’s complement is 9’s complement.
10’s complement is obtained by
10n-N
n = number of digits in the given number
N = given number
9’s complement is 10-1
Example: -7345
Sol: 2654- 9’s complement
2655-10’s complement
Ex: +565 same
Subtraction using 9’s complement and 10’s complement
Ex- 435-316
Sol: 435+(-316)
316 – compare the difference with 9
435+683=1118+1=1119
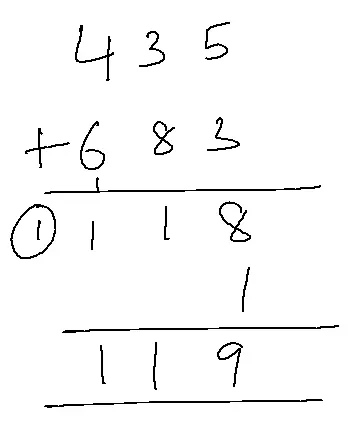
If a carry is generated in 9’s complement, the answer is the maximum value that can be reached by adding that carry.
If carry is not generated, the answer is negative, the final result is 9’s complement of that number.
In 10’s complement, if carry is generated ignore that carry. The answer is positive.
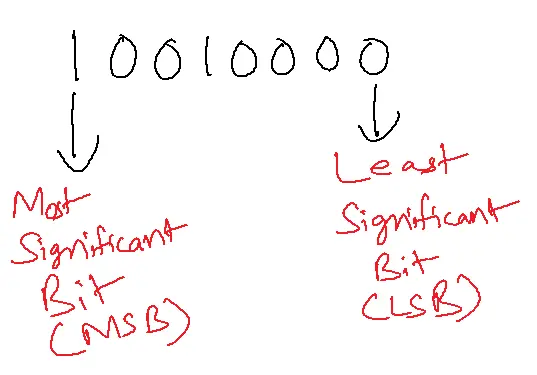
Representation of Negative numbers in Binary
- Sign Magnitude form
- 1’s Complement form
- 2’s Complement form
Sign Magnitude form
If a carry is generated in 9’s complement, the answer is the maximum value that can be reached by adding that carry.
0111
Here 0 indicates the sign of the number (positive), 1 indicates negative and 111 indicates the magnitude.
| Positive | Binary | Negative | Binary |
| 0 | 0000 | 0 | 1000 |
| 1 | 0001 | -1 | 1001 |
| 2 | 0010 | -2 | 1010 |
| 3 | 0011 | -3 | 1011 |
| 4 | 0100 | -4 | 1100 |
| 5 | 0101 | -5 | 1101 |
| 6 | 0110 | -6 | 1110 |
| 7 | 0111 | -7 | 1111 |
Range of Numbers: -(2n-1-1) to (2n-1-1)
1’s Complement form
Range of Numbers: -(2n-1) to (2n-1)
| +0 | 0000 | -0 | 1111 |
| +1 | 0001 | -1 | 1110 |
| +2 | 0010 | -2 | 1101 |
| +3 | 0011 | -3 | 1100 |
| +4 | 0100 | -4 | 1011 |
| +5 | 0101 | -5 | 1010 |
| +6 | 0110 | -6 | 1001 |
| +7 | 0111 | -7 | 1000 |
2’s Complement form
2’s complement of a number(binary) can be obtained by adding 1 to 1’s complement.

| +0 | 0000 | – | – |
| +1 | 0001 | -1 | 1111 |
| +2 | 0010 | -2 | 1110 |
| +3 | 0011 | -3 | 1101 |
| +4 | 0100 | -4 | 1100 |
| +5 | 0101 | -5 | 1011 |
| +6 | 0110 | -6 | 1010 |
| +7 | 0111 | -7 | 1001 |
Range of Numbers: -(2n-1) to (2n-1-1)
FAQs
1. What is Binary Addition?
- Binary addition of two or more binary numbers (numbers represented using only 0 and 1).
- It follows similar principles to decimal addition but uses a base-2 system.
- The fundamental rules are: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, and 1 + 1 = 10 (with a carry-over of 1).
2. How is Binary Addition performed?
- Binary addition is performed column by column, starting from the rightmost (least significant bit).
- Each column’s addition results in a sum bit and a carry bit (if applicable). The carry bit is added to the next column’s addition.
3. What is Hexadecimal Addition?
- Hexadecimal addition involves adding two or more hexadecimal numbers (numbers represented using 0-9 and A-F, where A=10, B=11… F=15).
- It utilizes a base-16 system. Similar to binary addition, it’s done column-wise, with carry-overs when the sum exceeds 15.
4. Why are Binary and Hexadecimal Addition important in digital logic design?
- Digital systems fundamentally operate on binary numbers. Binary addition is the core of arithmetic operations in computers and digital circuits.
- Hexadecimal is a compact way to represent binary data, making it easier for humans to read and write. Hexadecimal addition simplifies working with large binary numbers in programming and debugging.
5. How are Binary and Hexadecimal Adders implemented in digital circuits?
- Binary adders are built using logic gates like AND, OR, and XOR gates. The basic building blocks are half adders (add two single bits) and full adders (add three bits, including a carry-in).
- Hexadecimal adders can be constructed by combining multiple binary adders or using specialized circuits designed for hexadecimal arithmetic.
