A BCD (Binary Coded Decimal) Adder is a digital circuit that performs addition on binary-coded decimal numbers. BCD is a way to represent decimal numbers using binary digits (0s and 1s).
In BCD, each decimal digit (0-9) is represented by a 4-bit binary code.
A BCD Adder takes two BCD numbers as input, adds them, and produces a BCD result. The adder must follow the rules of decimal arithmetic, handling carries, and overflow.
The result may not be in BCD when we add two BCD numbers.
BCD Sum ≤9, no need to add 6.
BCD sum >9, add 6 to keep the result in BCD.
Table of Contents
Examples
6-0110
3-0011
If we add 6 and 3, the result is 9-1001, a valid BCD. [No need to add 6]
If we add 7 and 8
7-0111
8-1000
1111-not valid BCD
+6-0110
0101 carry-1 is a valid BCD.
| K | Z8 | Z4 | Z2 | Z1 | C | S8 | S4 | S2 | S1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 4 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 5 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 6 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 7 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 8 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 9 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 10 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 11 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 12 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 13 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 14 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 15 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 16 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 17 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 18 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 19 |
C=K+Z8Z4+Z8Z2
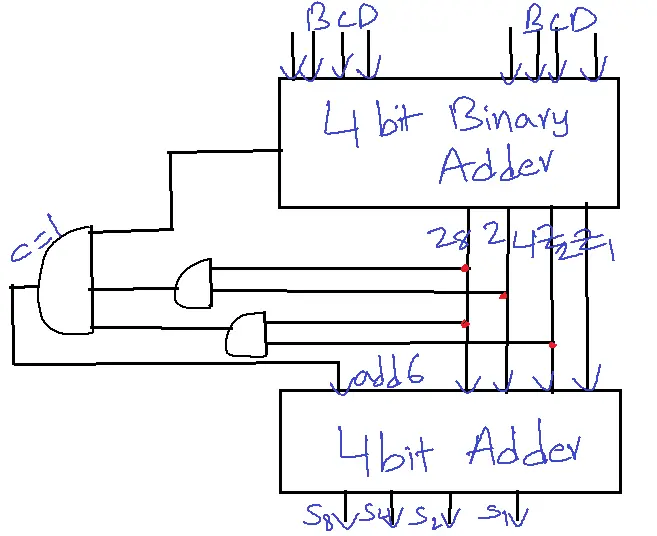
carry coming out of the bottom 4-bit adder can be ignored because that information is already available at c.
Advantages of BCD Adder
1. Easy to understand and implement: These Adders are simple to design and implement, making them a great choice for beginners.
2. Fast and efficient: These Adders perform calculations quickly, making them suitable for real-time applications.
3. Accurate decimal arithmetic: These Adders ensure accurate decimal calculations, key for financial, commercial, and scientific applications.
4. Simple to troubleshoot: With a straightforward design, these Adders are easy to debug and maintain.
5. Low power consumption: These Adders consume less power than other adder circuits.
6. Small silicon area: These Adders require minimal space on an integrated circuit, making them ideal for compact designs.
7. No need for binary-to-decimal conversion: These Adders work directly with decimal numbers, eliminating the need for conversions.
8. Easy to interface with decimal devices: These Adders can directly connect with decimal displays, keyboards, and other devices.
9. Suitable for low-speed applications: Calculators and digital meters are two examples of devices where these adders are ideal since speed is not a factor.
10. Cost-effective: These Adders are often less expensive to design and implement than other adder circuits.
Disadvantages of BCD Adder
1. Limited range: These Adders can only handle decimal numbers (0-9), limiting their range.
2. Inefficient for large numbers: These Adders become cumbersome and slow when dealing with large numbers.
3. Not suitable for binary arithmetic: These Adders are designed for decimal arithmetic, making them incompatible with binary operations.
4. More complex for multi-digit operations: These Adders require additional logic for multi-digit calculations, increasing complexity.
5. Slower than binary adders: These Adders are generally slower than binary adders due to the additional logic required.
6. Less flexible: These Adders are designed for specific decimal operations, limiting flexibility.
7. Not suitable for floating-point calculations: Floating-point arithmetic is not intended for use with these Adders.
8. More difficult to scale: These Adders become increasingly complex and difficult for large calculations.
9. Limited application: These Adders are mainly used in specific applications like calculators, digital meters, and financial calculators.
10. Less widely used: These Adders are less commonly used when compared to binary adders, making them less familiar to designers.
Applications of BCD Adder
1. Calculators: BCD Adders are used in calculator circuits for decimal arithmetic.
2. Digital Meters: BCD Adders measure and display decimal values in digital meters.
3. Financial Calculators: BCD Adders perform decimal calculations for financial applications.
4. Cash Registers: BCD Adders handle decimal arithmetic for cash register operations.
5. Digital Scales: BCD Adders calculate decimal weights in digital scales.
6. Timekeeping Devices: BCD Adders manage decimal time calculations in clocks and watches.
7. Decimal Displays: BCD Adders drive decimal displays in various applications.
8. Embedded Systems: BCD Adders are used in embedded systems requiring decimal arithmetic.
9. Measurement Instruments: BCD Adders measure and calculate decimal values in measurement instruments.
10. Legacy Systems: BCD Adders are still used in older systems where decimal arithmetic is required.
BCD Adders are suitable for applications where:
– Decimal arithmetic is essential
– Speed is not critical
– Simple calculations are required
– Space and power consumption are limited
Keep in mind that BCD Adders have limitations, and binary adders or other arithmetic circuits might be more suitable for applications requiring:
– High-speed calculations
– Large number handling
– Binary arithmetic
– Floating-point calculations
FAQs
1. What is a BCD adder?
- A BCD adder is a digital circuit designed to add two Binary Coded Decimal (BCD) numbers and produce a BCD-coded sum.
- Unlike a standard binary adder, a BCD adder accounts for the unique representation of decimal digits in BCD format (0-9), ensuring accurate decimal arithmetic operations.
2. How does a BCD adder work?
- A BCD adder typically comprises two 4-bit binary adders and additional correction logic.
- It first performs binary addition on the two BCD inputs. If the sum exceeds 9 or a carry-out is generated, the correction logic adds 6 (0110 in binary) to the sum to adjust it back into the valid BCD range.
3. Why do we need BCD adders?
- BCD adders are essential when dealing with decimal calculations in digital systems.
- These converters directly produce results in BCD format, frequently needed for displays or compatibility with devices using decimal representation.
4. What are the applications of BCD adders?
BCD adders find applications in various areas, including:
- Calculators: They are used in digital calculators to perform decimal arithmetic operations.
- Digital clocks and timers: They keep track of time and perform time-based calculations in BCD format.
- Digital displays: Their primary function is to handle and display numerical data using the decimal system.
- Industrial control systems: BCD encoders are indispensable in industrial settings where representing data in decimal format is crucial.
5. What are the challenges in designing BCD adders?
Designing BCD adders presents some challenges, including:
- Correction logic: Implementing the correction logic to handle sums exceeding 9 or carry-outs requires additional circuitry and can introduce some complexity.
- Speed: BCD adders can be slower than binary adders due to the additional correction steps involved.
